
Question and Answers Forum
Question Number 184144 by paul2222 last updated on 03/Jan/23
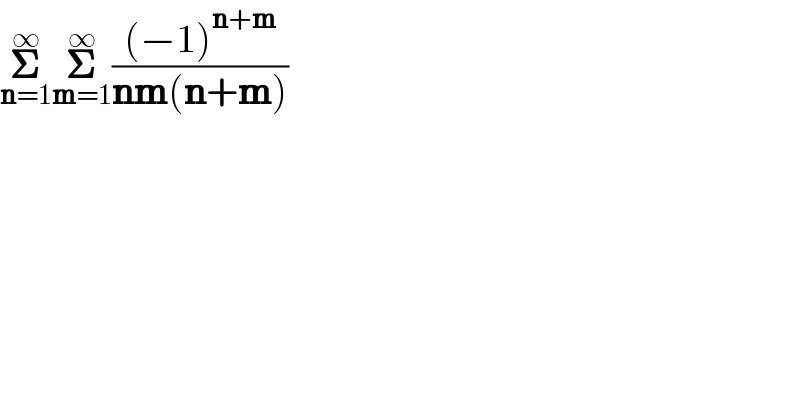
Answered by SEKRET last updated on 04/Jan/23

Commented by paul2222 last updated on 11/Jan/23

Answered by witcher3 last updated on 05/Jan/23
![∫_0 ^1 ((ln^2 (1+x))/x)dx=−li_2 (−x)ln(1+x)+∫_0 ^1 ((li_2 (−x))/(1+x))dx....(E) Li_2 (−x)=ζ(2)−ln(1+x)ln(−x)−li_2 (1+x) =li_2 (−x)ln(1+x)−Li_3 (1+x)+ζ(2)ln(1+x) −∫_0 ^1 ((ln(1+x))/(1+x))ln(−x) =−(1/2)ln^2 (1+x)ln(−x)+(1/2)∫((ln^2 (1+x))/x)dx =−2li_2 (−x)ln(1+x)−2Li_3 (1+x)+2ζ(2)ln(1+x)−ln^2 (1+x)ln(−x) li_2 (−x)=ζ(2)−ln(−x)ln(1+x)−li_2 (1+x) ∫((ln^2 (1+x))/x)dx=−2li_3 (1+x)+2li_2 (1+x)ln(1+x)+ln^2 (1+x)ln(−x)+c Let f(x)=Σ_(n≥1) Σ_(m≥1) (((−1)^(n+m) x^(n+m) )/(nm(n+m))),∀x∈[−1,1] f′(x)=ΣΣ(((−1)^(n+m) )/(nm))x^(n+m−1) =(1/x)ΣΣ(((−x)^n (−x)^m )/(n.m)) =(1/x){Σ(((−x)^n )/n)}{Σ(((−x)^m )/m)} Σ_(n≥1) (((−1)^(n−1) x^n )/n)=ln(1+x) f^′ (x)=((ln^(2() (1+x))/x) f(x)=∫((ln^2 (1+x))/x)dx...(E) apply f(x)=−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+c f(0)=0 lim_(x→0) {−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+c}=0 ⇔c−2ζ(3)=0 c=2ζ(3) f(x)=−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+2ζ(3) our Sum=f(1)](Q184343.png)
| ||
Question and Answers Forum | ||
Question Number 184144 by paul2222 last updated on 03/Jan/23 | ||
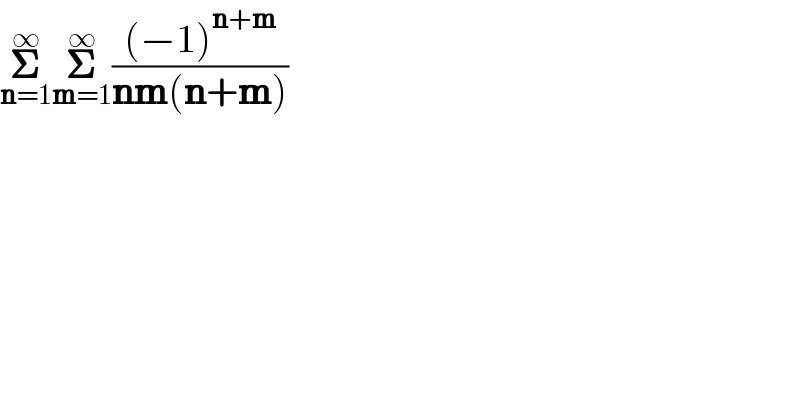 | ||
Answered by SEKRET last updated on 04/Jan/23 | ||
 | ||
| ||
Commented by paul2222 last updated on 11/Jan/23 | ||
 | ||
Answered by witcher3 last updated on 05/Jan/23 | ||
![∫_0 ^1 ((ln^2 (1+x))/x)dx=−li_2 (−x)ln(1+x)+∫_0 ^1 ((li_2 (−x))/(1+x))dx....(E) Li_2 (−x)=ζ(2)−ln(1+x)ln(−x)−li_2 (1+x) =li_2 (−x)ln(1+x)−Li_3 (1+x)+ζ(2)ln(1+x) −∫_0 ^1 ((ln(1+x))/(1+x))ln(−x) =−(1/2)ln^2 (1+x)ln(−x)+(1/2)∫((ln^2 (1+x))/x)dx =−2li_2 (−x)ln(1+x)−2Li_3 (1+x)+2ζ(2)ln(1+x)−ln^2 (1+x)ln(−x) li_2 (−x)=ζ(2)−ln(−x)ln(1+x)−li_2 (1+x) ∫((ln^2 (1+x))/x)dx=−2li_3 (1+x)+2li_2 (1+x)ln(1+x)+ln^2 (1+x)ln(−x)+c Let f(x)=Σ_(n≥1) Σ_(m≥1) (((−1)^(n+m) x^(n+m) )/(nm(n+m))),∀x∈[−1,1] f′(x)=ΣΣ(((−1)^(n+m) )/(nm))x^(n+m−1) =(1/x)ΣΣ(((−x)^n (−x)^m )/(n.m)) =(1/x){Σ(((−x)^n )/n)}{Σ(((−x)^m )/m)} Σ_(n≥1) (((−1)^(n−1) x^n )/n)=ln(1+x) f^′ (x)=((ln^(2() (1+x))/x) f(x)=∫((ln^2 (1+x))/x)dx...(E) apply f(x)=−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+c f(0)=0 lim_(x→0) {−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+c}=0 ⇔c−2ζ(3)=0 c=2ζ(3) f(x)=−2Li_3 (1+x)+2Li_2 (1+x)ln(1+x)+ln(−x)ln^2 (1+x)+2ζ(3) our Sum=f(1)](Q184343.png) | ||
| ||