
Question and Answers Forum
Question Number 184280 by mr W last updated on 04/Jan/23
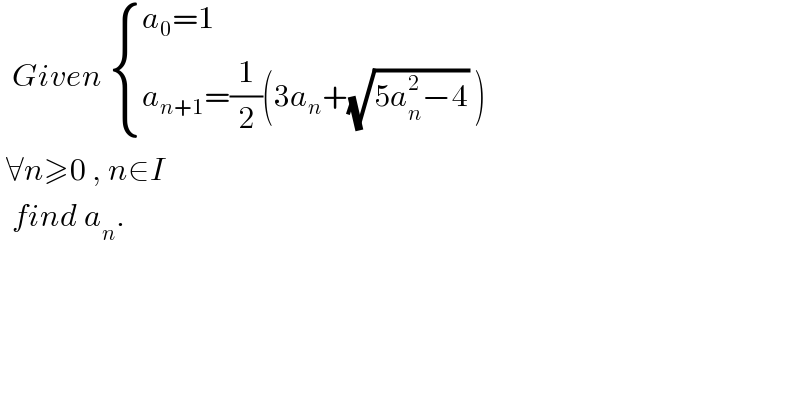
Commented by mr W last updated on 04/Jan/23

Commented by mr W last updated on 04/Jan/23
![i found finally a solution: a_n =(2/( (√5))) cosh [(2n+1) cosh^(−1) ((√5)/2) ] which delivers: a_0 =1 a_1 =2 a_2 =5 a_3 =13 a_4 =34 a_5 =89 ...](Q184283.png)
Commented by mr W last updated on 04/Jan/23
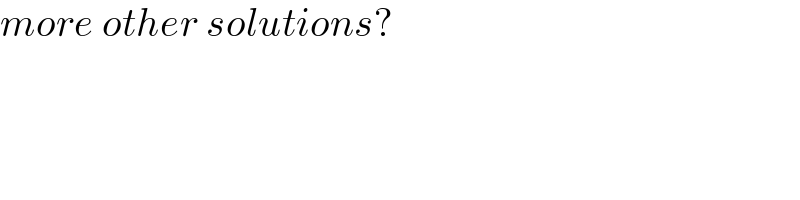
Commented by SEKRET last updated on 04/Jan/23

Commented by SEKRET last updated on 04/Jan/23

Commented by SEKRET last updated on 04/Jan/23
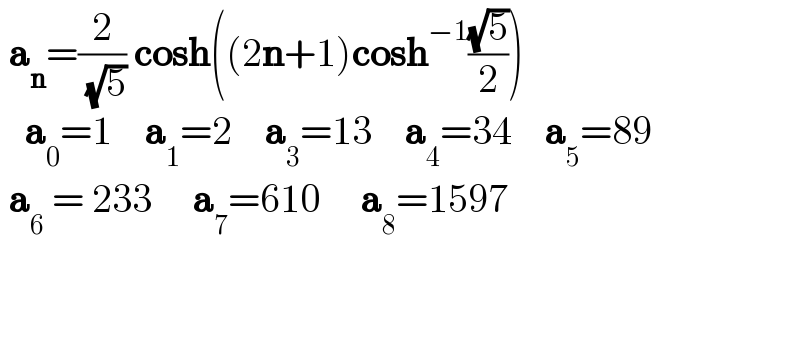
Commented by SEKRET last updated on 04/Jan/23
Commented by mr W last updated on 04/Jan/23
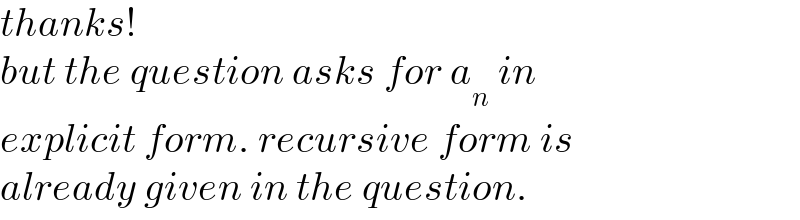
Commented by SEKRET last updated on 04/Jan/23

Commented by Frix last updated on 04/Jan/23
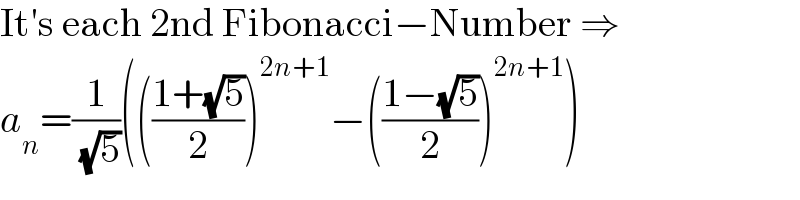
Commented by mr W last updated on 04/Jan/23
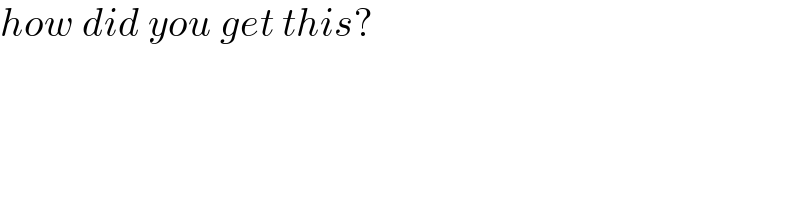
Commented by manxsol last updated on 05/Jan/23

Commented by mr W last updated on 05/Jan/23

Answered by mr W last updated on 05/Jan/23
![a_(n+1) =(1/2)(3a_n +(√(5a_n ^2 −4))) 2a_(n+1) −3a_n =(√(5a_n ^2 −4)) a_(n+1) ^2 −3a_(n+1) a_n +a_n ^2 +1=0 (a_(n+1) −a_n )^2 +1=a_(n+1) a_n let a_(n+1) +a_n =u a_(n+1) −a_n =v ⇒u^2 −5v^2 =4 ((u/2))^2 −((((√5)v)/2))^2 =1 cosh^2 x_n −sinh^2 x_n =1 (u/2)=cosh x_n ⇒u=2 cosh x_n (((√5)v)/2)=sinh x_n ⇒v=((2 sinh x_n )/( (√5))) a_n =(1/2)(u−v)=cosh x_n −((sinh x_n )/( (√5))) a_n =(2/( (√5)))(((√5)/2) cosh x_n −(1/2) sinh x_n ) a_n =(2/( (√5)))(cosh x_n cosh α−sinh x_n sinh α)=kcosh (x_n −α) a_n =(2/( (√5))) cosh (x_n −α) with α=cosh^(−1) ((√5)/2) a_(n+1) =(1/2)(u+v)=cosh x_n +((sinh x_n )/( (√5))) a_(n+1) =(2/( (√5)))(((√5)/2) cosh x_n +(1/2) sinh x_n ) a_(n+1) =(2/( (√5))) (cosh x_n cosh α+sinh x_n sinh α) a_(n+1) =(2/( (√5))) cosh (x_n +α) on the other side: a_(n+1) =(2/( (√5))) cosh (x_(n+1) −α) ⇒cosh (x_(n+1) −α)=cosh (x_n +α) ⇒x_(n+1) −α=x_n +α ⇒x_(n+1) =x_n +2α ← A.P. with c.d. =2α ⇒x_n =x_0 +2nα a_n =(2/( (√5))) cosh (x_0 +2nα−α) ⇒a_n =(2/( (√5))) cosh [x_0 +(2n−1) cosh^(−1) ((√5)/2)] a_0 =(2/( (√5))) cosh (x_0 −cosh^(−1) ((√5)/2))=1 ⇒x_0 =2 cosh^(−1) ((√5)/2) ⇒a_n =(2/( (√5))) cosh [(2n+1)cosh^(−1) ((√5)/2)] additionally: cosh^(−1) ((√5)/2)=ln (((√5)/2)+(√((((√5)/2))^2 −1)))=ln (((√5)+1)/2) (2n+1)cosh^(−1) ((√5)/2)=ln ((((√5)+1)/2))^((2n+1)) e^(−(2n+1)cosh^(−1) ((√5)/2)) =((((√5)+1)/2))^(−(2n+1)) =((((√5)−1)/2))^((2n+1)) a_n =(2/( (√5))) cosh [(2n+1)cosh^(−1) ((√5)/2)] a_n =(1/( (√5)))[e^((2n+1)cosh^(−1) ((√5)/2)) +e^(−(2n+1)cosh^(−1) ((√5)/2)) ] ⇒a_n =(1/( (√5)))[((((√5)+1)/2))^((2n+1)) +((((√5)−1)/2))^((2n+1)) ]](Q184294.png)
Commented by SEKRET last updated on 05/Jan/23

Commented by Frix last updated on 05/Jan/23
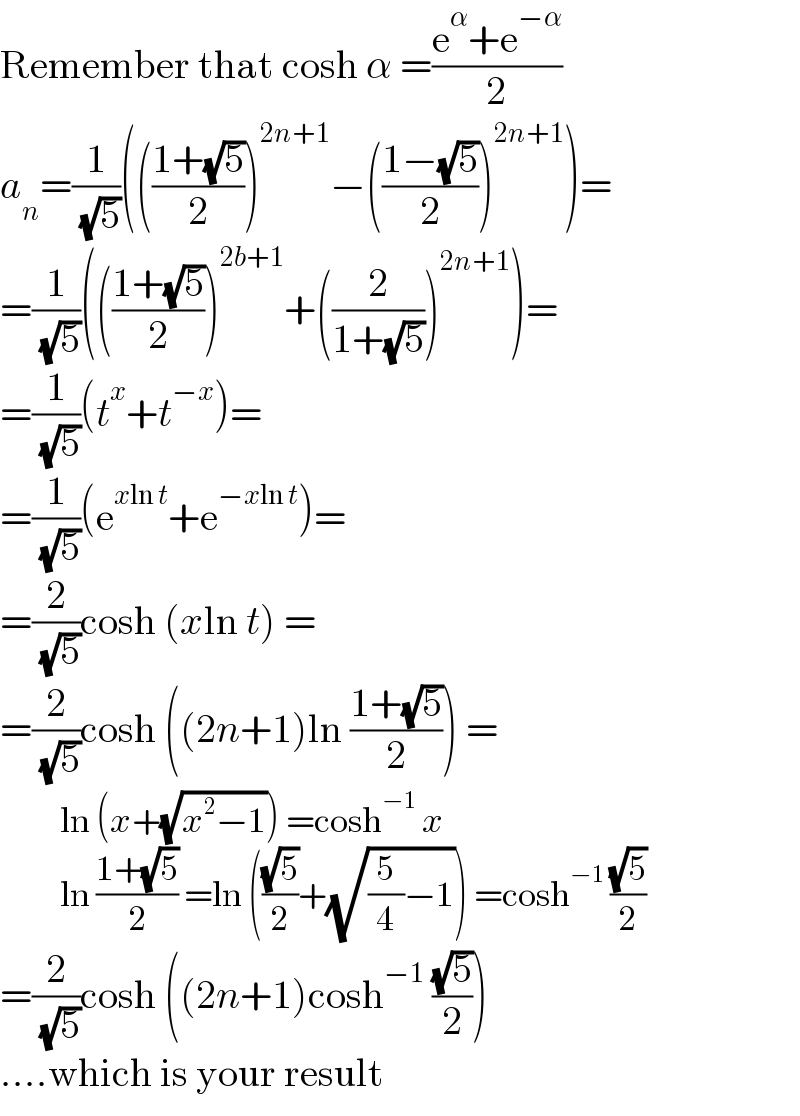
Commented by mr W last updated on 05/Jan/23
![thanks sir! i′ve also added the deduction to a_n =(1/( (√5)))[((((√5)+1)/2))^((2n+1)) +((((√5)−1)/2))^((2n+1)) ]. see above.](Q184323.png)
