Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mensuration Questions
Previous in All Question Next in All Question
Previous in Mensuration Next in Mensuration
Question Number 184387 by ajfour last updated on 05/Jan/23

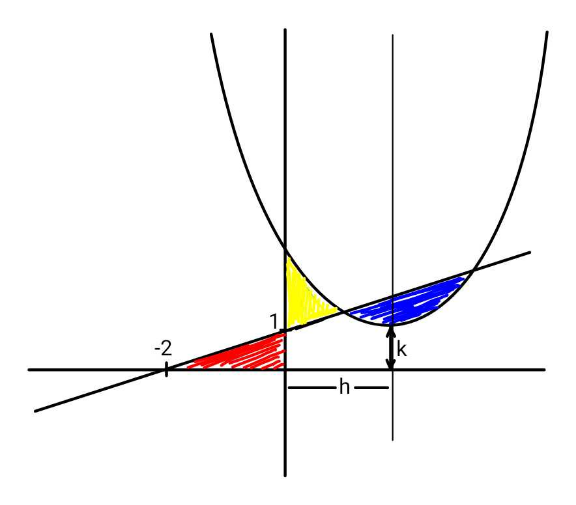
Commented by ajfour last updated on 05/Jan/23

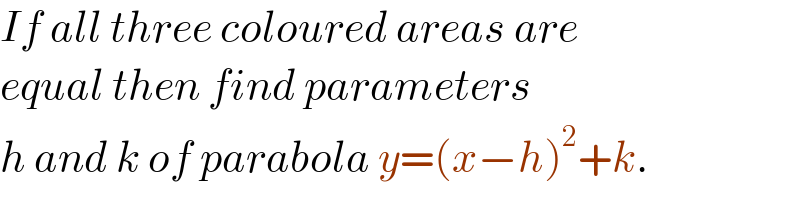
$I f a l l t h r e e c o l o u r e d a r e a s a r e$ $e q u a l t h e n f i n d p a r a m e t e r s$ $h a n d k o f p a r a b o l a y = {(x - h)}^{2} + k .$
	Answered by mr W last updated on 06/Jan/23

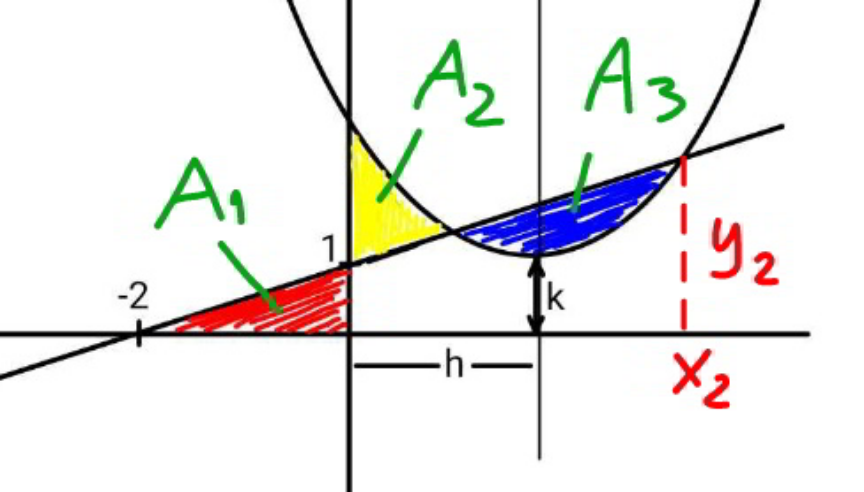
	Commented by mr W last updated on 06/Jan/23

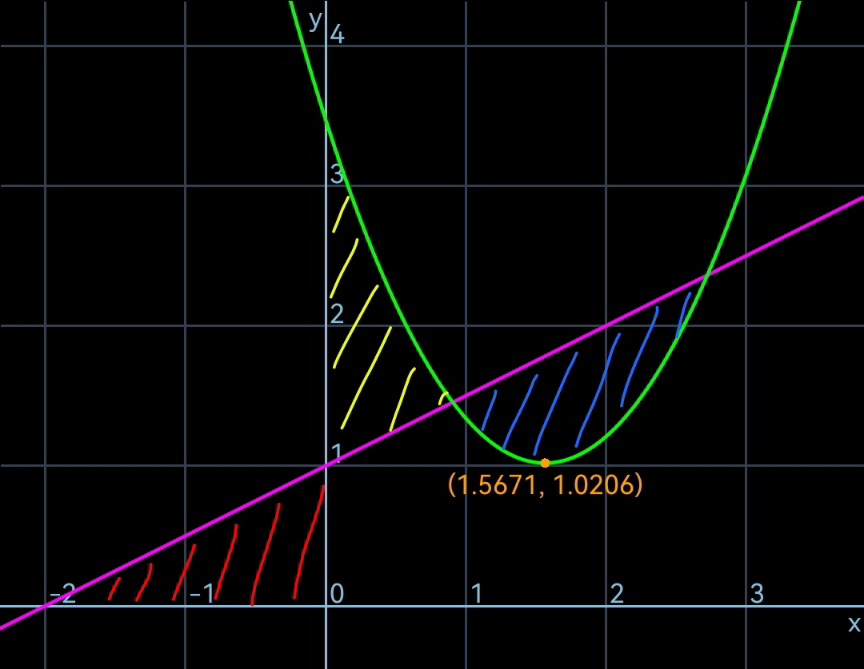
	Commented by mr W last updated on 07/Jan/23

	$a r e a o f r e d t r i a n g l e A_{1} = \frac{2 \times 1}{2} = 1$ $e q n . o f l i n e :$ $y = \frac{x}{2} + 1$ $e q n . o f p a r a b o l a :$ $y = {(x - h)}^{2} + k$ $i n t e r s e c t i o n o f l i n e a n d p a r a b o l a :$ ${(x - h)}^{2} + k = \frac{x}{2} + 1$ ${(x - h)}^{2} - \frac{(x - h)}{2} + (k - 1 - \frac{h}{2}) = 0$ $\Rightarrow x_{2} - h = \frac{1}{4} + \frac{1}{4} \sqrt{17 + 8 h - 16 k}$ $\Rightarrow y_{2} = \frac{9}{8} + \frac{h}{2} + \frac{1}{8} \sqrt{17 + 8 h - 16 k}$ $a r e a o f b l u e r e g i o n :$ $A_{3} = \frac{1}{6} {[\frac{1}{4} - 4 (k - 1 - \frac{h}{2})]}^{3 / 2} = A_{1} = 1$ $\frac{1}{6} {[\frac{1}{4} - 4 (k - 1 - \frac{h}{2})]}^{3 / 2} = 1$ $17 - 16 k + 8 h = 4 \sqrt[3]{36}$ $\Rightarrow k = \frac{h}{2} + \frac{17}{16} - \frac{\sqrt[3]{36}}{4}$ $\Rightarrow x_{2} = h + \frac{1}{4} + \frac{\sqrt[3]{6}}{2}$ $\Rightarrow y_{2} = \frac{h}{2} + \frac{9}{8} + \frac{\sqrt[3]{6}}{4}$ $s i n c e A_{2} = A_{3}, a r e a u n d e r t h e p a r a b o l a$ $i s e q u a l t o a r e a u n d e r t h e l i n e f r o m$ $x = 0 t o x = x_{2} .$ $x_{2} k + \frac{h^{3}}{3} + \frac{{(x_{2} - h)}^{3}}{3} = \frac{(1 + y_{2}) x_{2}}{2}$ $(h + \frac{1}{4} + \frac{\sqrt[3]{6}}{2}) (\frac{h}{2} + \frac{17}{16} - \frac{\sqrt[3]{36}}{4}) + \frac{h^{3}}{3} + \frac{{(\frac{1}{4} + \frac{\sqrt[3]{6}}{2})}^{3}}{3} = \frac{(1 + \frac{h}{2} + \frac{9}{8} + \frac{\sqrt[3]{6}}{4}) (h + \frac{1}{4} + \frac{\sqrt[3]{6}}{2})}{2}$ $\Rightarrow h^{3} + \frac{3}{4} (h + \frac{1}{4} + \frac{\sqrt[3]{6}}{2}) (h - \frac{\sqrt[3]{6}}{2} - \sqrt[3]{36}) + {(\frac{1}{4} + \frac{\sqrt[3]{6}}{2})}^{3} = 0$ $s i n c e t h i s i s a c u b i c e q u a t i o n f o r h,$ $e x a c t s o l u t i o n i s p o s s i b l e, b u t v e r y$ $c o m p l i c a t e d . w e g e t a p p r o x i m a t e l y$ $h \approx 1.5671, k \approx 1.0206$
	Commented by ajfour last updated on 06/Jan/23

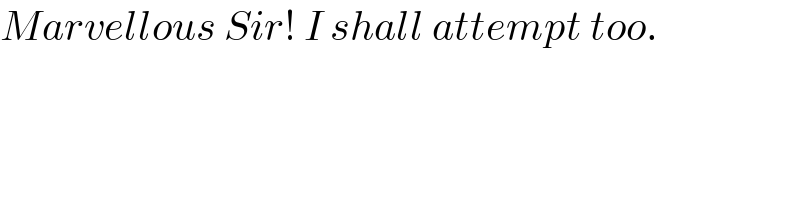
	$M a r v e l l o u s S i r! I s h a l l a t t e m p t t o o .$
	Answered by ajfour last updated on 07/Jan/23
	$If vertex of parabola is Origin. y=x^2 [eq. of parabola] y=(x/2)+(1+(h/2)−k) [eq. of line] say 1+(h/2)−k=m t^2 =(t/2)+m ∫_(−h) ^( t) (x^2 −(x/2)−m)dx=A (=0,1) ((t^3 /3)−(t^2 /4)+mt)+((h^3 /3)+(h^2 /4)+mh)=A ⇒ (t^3 /3)−(t^2 /4)+t^3 −(t^2 /2) +((h^3 /3)+(h^2 /4)+t^2 h−((th)/2))=A ⇒ (t+h){((t^2 −th+h^2 )/3)−(((t−h))/4) +t^2 −(t/2)}=A For A=0, t=t_2 as t+h≠0 ⇒ 4(t^2 −th+h^2 )+12t^2 +3h=6t+3t ⇒ 16t^2 −4th+4h^2 =9t−3h ⇒ 4((t^2 /h^2 )−(t/h)+1)=(3/h)(((3t)/h)−1) say (t/h)=s 4s^2 −(4+(9/h))s+(4+(3/h))=0 ⇒ s=(1/2)(1+(9/(4h)))±(√((1/4)(1+(9/(4h)))^2 −(1+(3/(4h))))) ⇒ 8hs=4h+9±(√((4h+9)^2 −16h(4h+3))) 8hs=4h+9±(√(81+24h−48h^2 )) ....$
	$I f v e r t e x o f p a r a b o l a i s O r i g i n .$ $y = x^{2} [e q . o f p a r a b o l a]$ $y = \frac{x}{2} + (1 + \frac{h}{2} - k) [e q . o f l i n e]$ $s a y 1 + \frac{h}{2} - k = m$ $t^{2} = \frac{t}{2} + m$ $\int_{- h}^{t} (x^{2} - \frac{x}{2} - m) d x = A (= 0, 1)$ $(\frac{t^{3}}{3} - \frac{t^{2}}{4} + m t) + (\frac{h^{3}}{3} + \frac{h^{2}}{4} + m h) = A$ $\Rightarrow \frac{t^{3}}{3} - \frac{t^{2}}{4} + t^{3} - \frac{t^{2}}{2}$ $+ (\frac{h^{3}}{3} + \frac{h^{2}}{4} + t^{2} h - \frac{t h}{2}) = A$ $\Rightarrow (t + h) {\frac{t^{2} - t h + h^{2}}{3} - \frac{(t - h)}{4}$ $+ t^{2} - \frac{t}{2}} = A$ $F o r A = 0, t = t_{2}$ $a s t + h \neq 0 \Rightarrow$ $4 (t^{2} - t h + h^{2}) + 12 t^{2} + 3 h = 6 t + 3 t$ $\Rightarrow 16 t^{2} - 4 t h + 4 h^{2} = 9 t - 3 h$ $\Rightarrow 4 (\frac{t^{2}}{h^{2}} - \frac{t}{h} + 1) = \frac{3}{h} (\frac{3 t}{h} - 1)$ $s a y \frac{t}{h} = s$ $4 s^{2} - (4 + \frac{9}{h}) s + (4 + \frac{3}{h}) = 0$ $\Rightarrow s = \frac{1}{2} (1 + \frac{9}{4 h}) \pm \sqrt{\frac{1}{4} {(1 + \frac{9}{4 h})}^{2} - (1 + \frac{3}{4 h})}$ $\Rightarrow 8 h s = 4 h + 9 \pm \sqrt{{(4 h + 9)}^{2} - 16 h (4 h + 3)}$ $8 h s = 4 h + 9 \pm \sqrt{81 + 24 h - 48 h^{2}}$ $. . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum