
Question and Answers Forum
Question Number 184523 by cortano1 last updated on 08/Jan/23

Answered by SEKRET last updated on 08/Jan/23
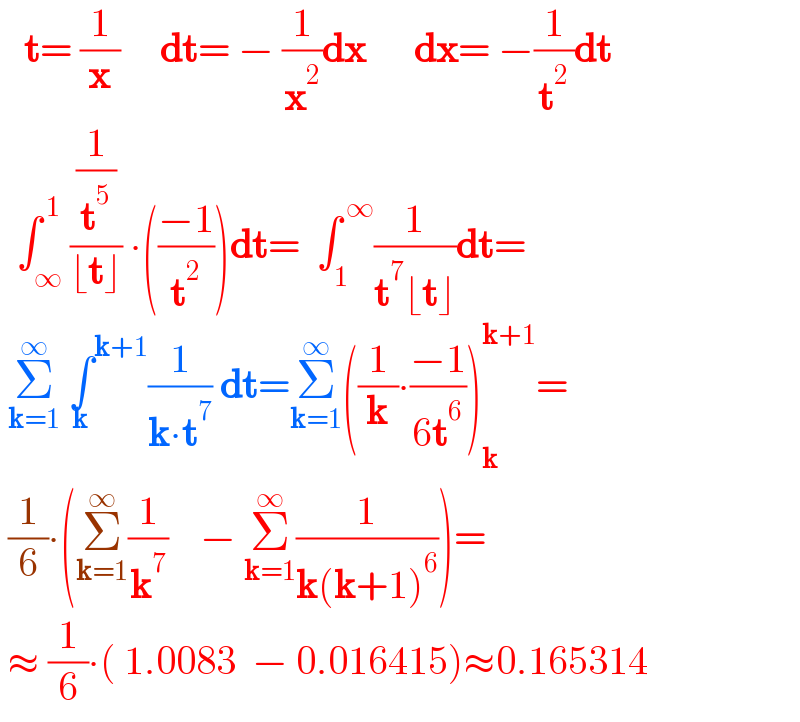
Answered by mr W last updated on 08/Jan/23
![I=∫_0 ^1 (x^5 /(⌊(1/x)⌋))dx=? let x=(1/t) dx=−(dt/t^2 ) I=∫_1 ^∞ (dt/(t^7 ⌊t⌋)) =Σ_(k=1) ^∞ ∫_k ^(k+1) (dt/(t^7 ⌊t⌋)) =Σ_(k=1) ^∞ (1/k)∫_k ^(k+1) (dt/t^7 ) =Σ_(k=1) ^∞ (1/k)[−(1/(6t^6 ))]_k ^(k+1) =(1/6)Σ_(k=1) ^∞ (1/k)[(1/k^6 )−(1/((k+1)^6 ))] =(1/6)Σ_(k=1) ^∞ [(1/k^7 )−(1/(k(k+1)^6 ))] =(1/6)(A−B) A=Σ_(k=1) ^∞ (1/k^7 )=ζ(7) ← Riemann Zeta function ζ(s)=Σ_(n=1) ^∞ (1/n^s ) B=Σ_(k=1) ^∞ (1/(k(k+1)^6 )) =Σ_(k=2) ^∞ (1/((k−1)k^6 )) =Σ_(k=2) ^∞ [(1/((k−1)))−(1/k)−(1/k^2 )−(1/k^3 )−(1/k^4 )−(1/k^5 )−(1/k^6 )] =Σ_(k=2) ^∞ (1/((k−1)))−Σ_(k=2) ^∞ (1/k)−Σ_(k=2) ^∞ ((1/k^2 )+(1/k^3 )+(1/k^4 )+(1/k^5 )+(1/k^6 )) =Σ_(k=1) ^∞ (1/k)−Σ_(k=1) ^∞ (1/k)+1−Σ_(k=1) ^∞ ((1/k^2 )+(1/k^3 )+(1/k^4 )+(1/k^5 )+(1/k^6 ))+5 =−[ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)]+6 I=(1/6)[ζ(7)+ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)−6] ⇒I=((ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)+ζ(7))/6)−1 ≈0.165322382919](Q184528.png)
| ||
Question and Answers Forum | ||
Question Number 184523 by cortano1 last updated on 08/Jan/23 | ||
 | ||
Answered by SEKRET last updated on 08/Jan/23 | ||
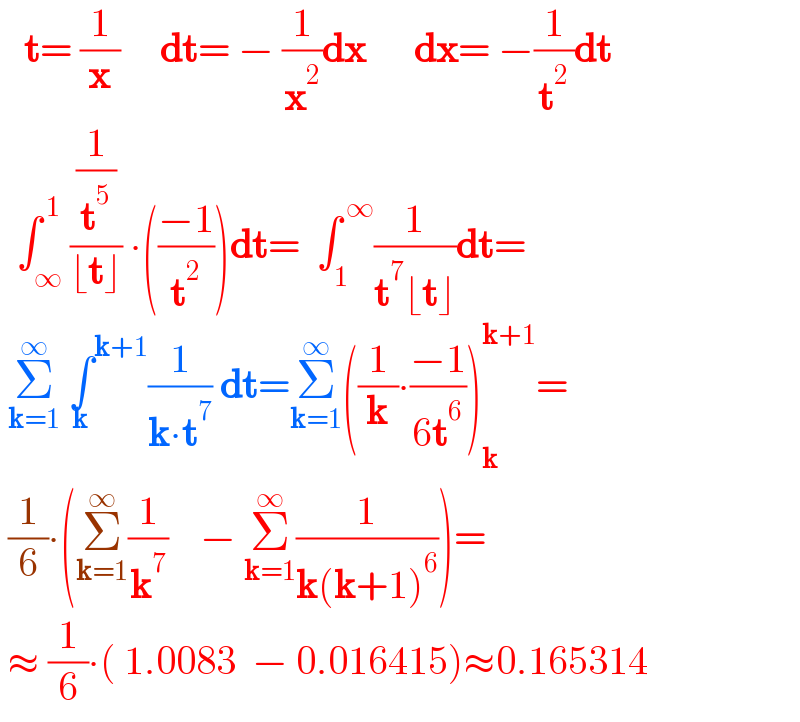 | ||
| ||
Answered by mr W last updated on 08/Jan/23 | ||
![I=∫_0 ^1 (x^5 /(⌊(1/x)⌋))dx=? let x=(1/t) dx=−(dt/t^2 ) I=∫_1 ^∞ (dt/(t^7 ⌊t⌋)) =Σ_(k=1) ^∞ ∫_k ^(k+1) (dt/(t^7 ⌊t⌋)) =Σ_(k=1) ^∞ (1/k)∫_k ^(k+1) (dt/t^7 ) =Σ_(k=1) ^∞ (1/k)[−(1/(6t^6 ))]_k ^(k+1) =(1/6)Σ_(k=1) ^∞ (1/k)[(1/k^6 )−(1/((k+1)^6 ))] =(1/6)Σ_(k=1) ^∞ [(1/k^7 )−(1/(k(k+1)^6 ))] =(1/6)(A−B) A=Σ_(k=1) ^∞ (1/k^7 )=ζ(7) ← Riemann Zeta function ζ(s)=Σ_(n=1) ^∞ (1/n^s ) B=Σ_(k=1) ^∞ (1/(k(k+1)^6 )) =Σ_(k=2) ^∞ (1/((k−1)k^6 )) =Σ_(k=2) ^∞ [(1/((k−1)))−(1/k)−(1/k^2 )−(1/k^3 )−(1/k^4 )−(1/k^5 )−(1/k^6 )] =Σ_(k=2) ^∞ (1/((k−1)))−Σ_(k=2) ^∞ (1/k)−Σ_(k=2) ^∞ ((1/k^2 )+(1/k^3 )+(1/k^4 )+(1/k^5 )+(1/k^6 )) =Σ_(k=1) ^∞ (1/k)−Σ_(k=1) ^∞ (1/k)+1−Σ_(k=1) ^∞ ((1/k^2 )+(1/k^3 )+(1/k^4 )+(1/k^5 )+(1/k^6 ))+5 =−[ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)]+6 I=(1/6)[ζ(7)+ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)−6] ⇒I=((ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)+ζ(7))/6)−1 ≈0.165322382919](Q184528.png) | ||
| ||