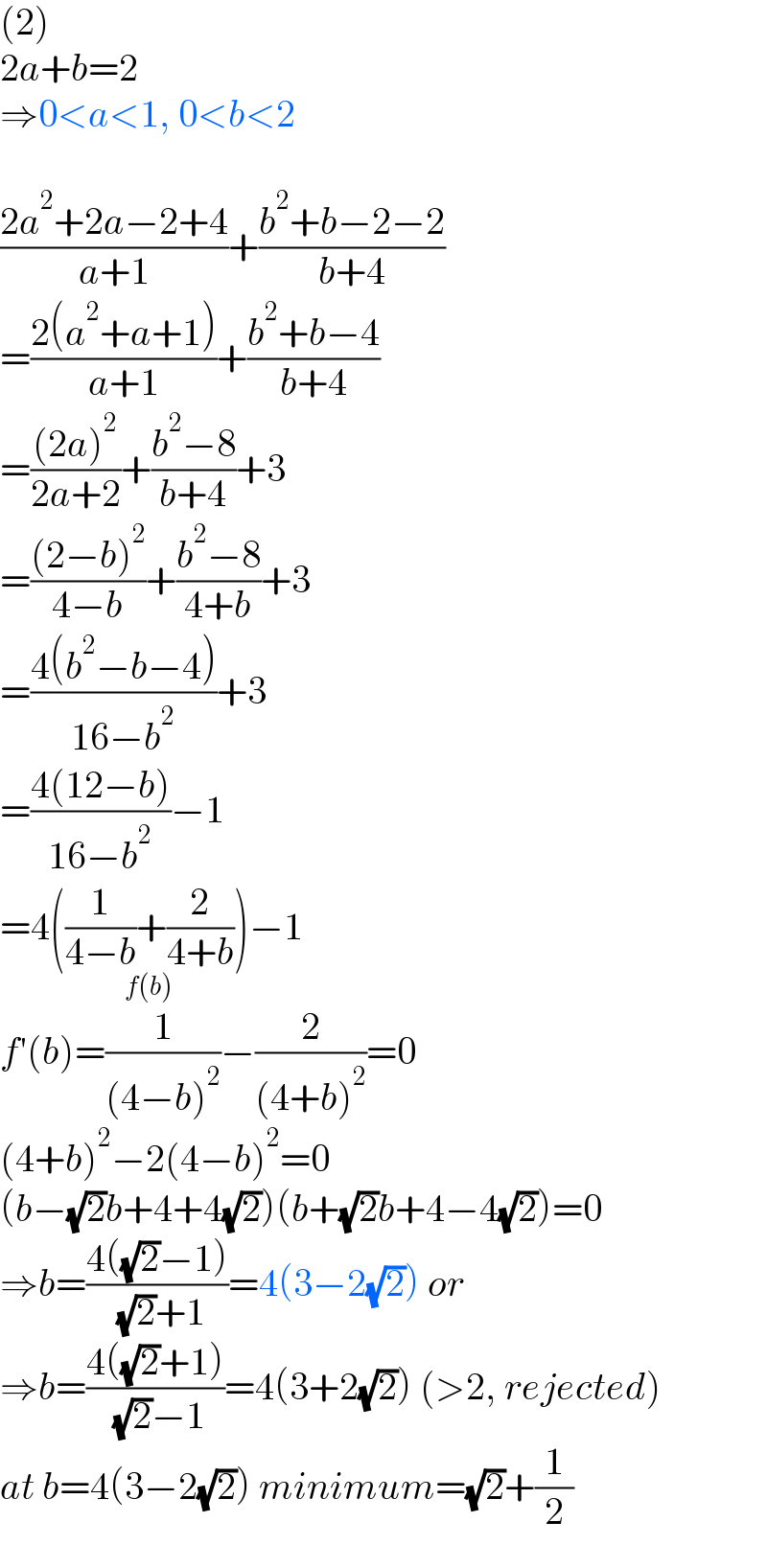Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 184535 by CrispyXYZ last updated on 08/Jan/23

$$\mathrm{If}a,b>0\mathrm{such}\mathrm{that}2a+b=2,$$ $$\mathrm{then}\mathrm{find}\mathrm{the}\mathrm{minimum}\mathrm{value}\mathrm{of}:$$ $$1)(4a^2+1)(b^2+1)$$ $$2)\frac{2a^2-b+4}{a+1}+\frac{b^2-2a-2}{b+4}$$

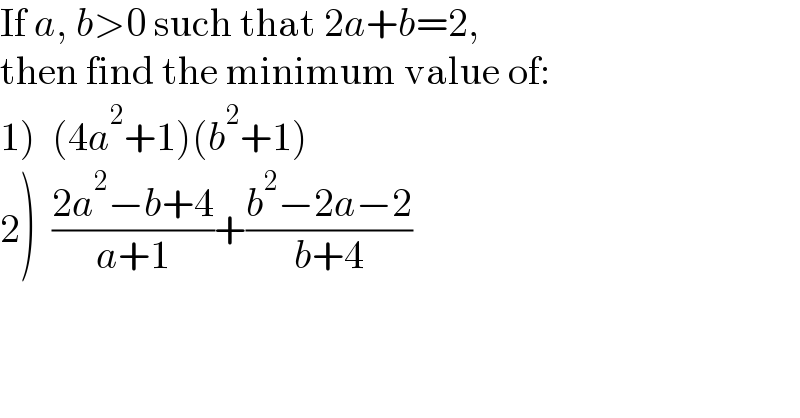
Answered by cortano1 last updated on 08/Jan/23

$$\left(1\right)\{\begin{array}{l}b=2-2a\\ f\left(a\right)=(4a^2+1)(4a^2-8a+5)\end{array}$$ $$f\left(a\right)=16a^4-32a^3+24a^2-8a+5$$ $$f{}^{\prime }\left(a\right)=64a^3-96a^2+48a-8=0$$ $$\Rightarrow a=\frac{1}{2};b=2-1=1$$ $$min\left\{(4a^2+1)(b^2+1)\right\}=2\times 2=4$$

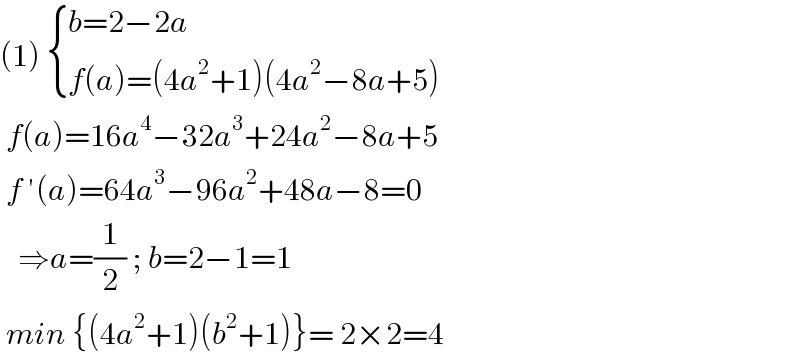
Answered by mr W last updated on 08/Jan/23

$$\left(1\right)$$ $$a+\frac{b}{2}=1$$ $$a={\cos }^2\theta$$ $$b=2{\sin }^2\theta$$ $$(4{\cos }^4\theta +1)(4{\sin }^4\theta +1)$$ $$=1+4({\cos }^4\theta +{\sin }^4\theta )+16{\left(\cos \theta \sin \theta \right)}^4$$ $$=1+4-2{\left(2\cos \theta \sin \theta \right)}^2+{\left(2\cos \theta \sin \theta \right)}^4$$ $$=5-2{\sin }^{2}2\theta +{\sin }^{4}2\theta$$ $$=4+{(1-{\sin }^{2}2\theta )}^2$$ $$=4+{\cos }^{4}2\theta ⩾4=minimum$$

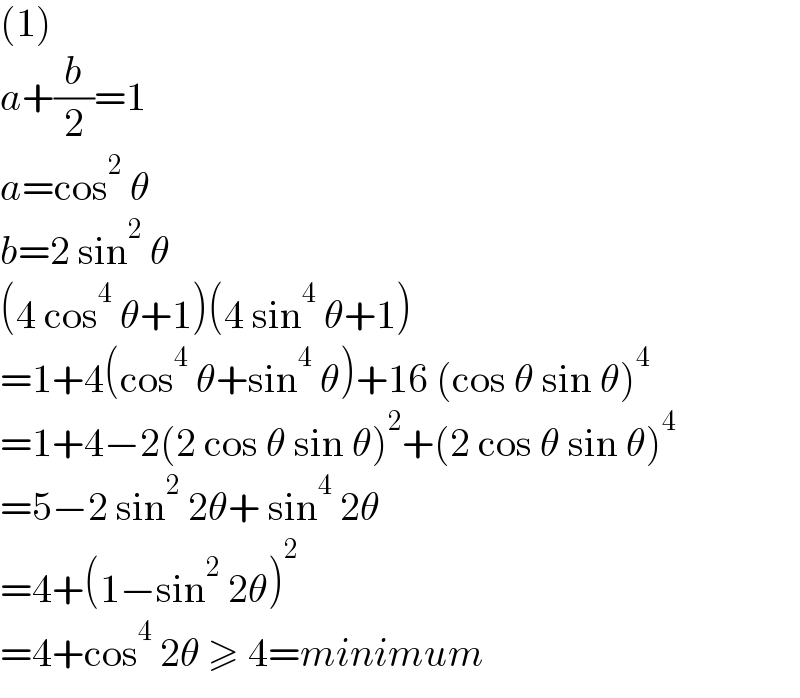
Answered by greougoury555 last updated on 08/Jan/23

$$\left(1\right)f(a,b,\lambda )=(4a^2+1)(b^2+1)+\lambda (2a+b-2)$$ $$\frac{\partial f}{\partial a}=8a(b^2+1)+2\lambda =0$$ $$\frac{\partial f}{\partial b}=2b(4a^2+1)+\lambda =0$$ $$\frac{\partial f}{\partial \lambda }=2a+b-2=0\Rightarrow b=2-2a$$ $$\Rightarrow -4a(b^2+1)=-2b(4a^2+1)$$ $$\Rightarrow a(4a^2-8a+5)=(1-a)(4a^2+1)$$ $$\Rightarrow 4a^3-8a^2+5a=-4a^3+4a^2-a+1$$ $$\Rightarrow 8a^3-12a^2+6a-1=0$$ $$\Rightarrow {(2a-1)}^3=0;a=\frac{1}{2}$$ $$\therefore minimum(4a^2+1)(b^2+1)=4$$

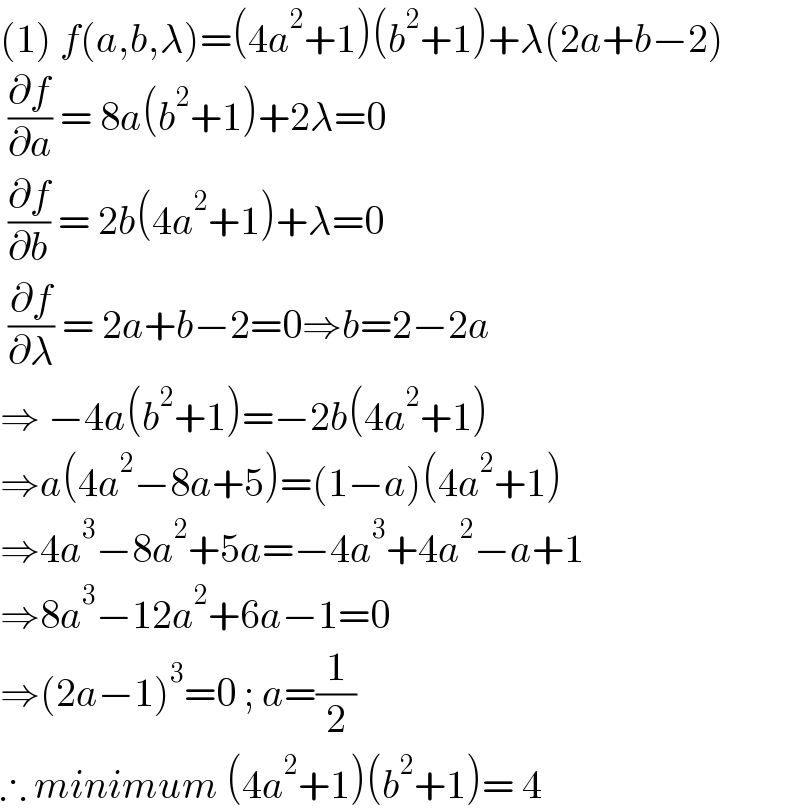
Answered by ajfour last updated on 08/Jan/23

$$1)$$ $$2a=t$$ $$t+b=2$$ $$(t^2+1)(b^2+1)isminimum$$ $$fort=b=1,so$$ $$theminimumis2\times 2=4$$ $$2)$$ $$f(t,b)=\frac{t^2-2b+8}{t+2}+\frac{b^2-t-2}{b+4}$$ $$lett+2=pb+4=q$$ $$p+q=8$$ $$f(p,q)=\frac{p^2-4p-2q+20}{p}+\frac{q^2-8q-p+16}{q}$$ $$=p-4+\frac{20}{p}-\frac{2q}{p}+q-8-\frac{p}{q}+\frac{16}{q}$$ $$=-4+\frac{20}{p}+\frac{16}{q}-\frac{2q}{p}-\frac{p}{q}$$ $$=-4+\frac{2(10-q)}{p}+\frac{(16-p)}{q}$$ $$=-4+\frac{2(2+p)}{p}+\frac{(8+q)}{q}$$ $$=-1+\frac{4}{p}+\frac{8}{q}$$ $$f\left(p\right)=-1+\frac{4}{p}+\frac{8}{8-p}$$ $$\frac{df}{dp}=-\frac{4}{p^2}+\frac{8}{{(8-p)}^2}=0$$ $$\Rightarrow \frac{8-p}{p}=\pm \sqrt{2}$$ $$p=\frac{8}{1+\sqrt{2}}orp=-\frac{8}{(\sqrt{2}-1)}$$ $$f_1=-1+\frac{4}{p}+\frac{8}{8-p}=\frac{1+\sqrt{2}}{2}+\frac{1}{1-\frac{1}{1+\sqrt{2}}}$$ $$=-1+\frac{1+\sqrt{2}}{2}+\frac{1+\sqrt{2}}{\sqrt{2}}=\frac{1}{2}+\sqrt{2}$$ $$f_2=-1-\frac{(\sqrt{2}-1)}{2}+\frac{1}{1+\frac{1}{\sqrt{2}-1}}$$ $$=-1+\frac{1-\sqrt{2}+2-\sqrt{2}}{2}=\frac{1}{2}-\sqrt{2}$$ $$$$

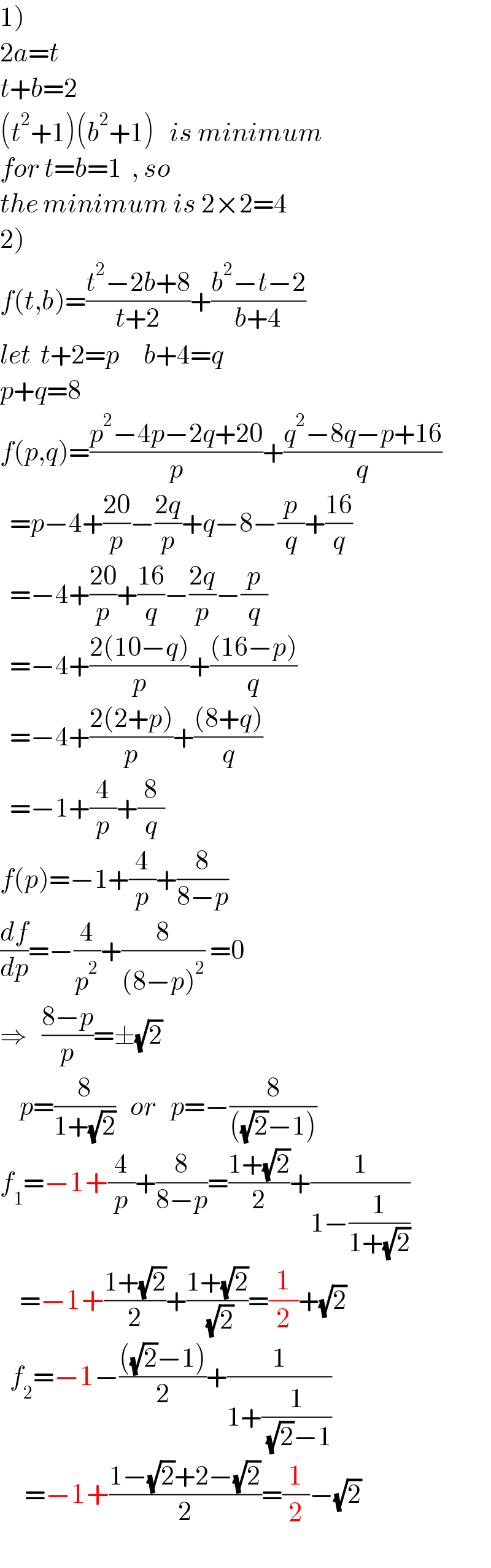
Commented bymr W last updated on 08/Jan/23

$$pleaserecheckhere:$$ $$f(t,b)=\frac{t^2/2-2b+8}{t+2}+\frac{b^2-t-2}{b+4}$$ $$ithinkfor\left(2\right)thereisnonicelooking$$ $$solution.$$

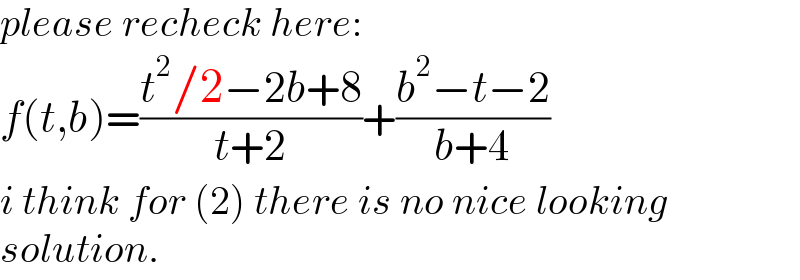
Commented byajfour last updated on 08/Jan/23

$$nosirf(t,b)=\frac{t^2-2b+8}{t+2}$$ $$=\frac{4a^2-2b+8}{2a+2}$$

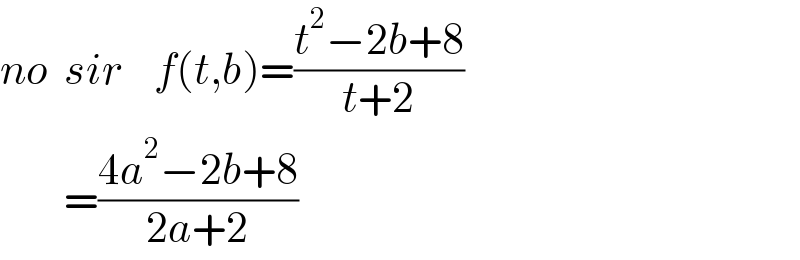
Commented bymr W last updated on 08/Jan/23

$$yes,youareright.$$

Answered by Frix last updated on 08/Jan/23

$$2)$$ $$b=2-2a$$ $$\Rightarrow$$ $$-\frac{a^2+7}{(a+1)(a-3)}$$ $$\frac{d[-\frac{a^2+7}{(a+1)(a-3)}]}{da}=\frac{2(a^2+10a-7)}{{(a+1)}^2{(a-3)}^2}=0$$ $$\Rightarrow$$ $$a=-5\pm 4\sqrt{2}$$ $$\mathrm{local}\max =\frac{1}{2}-\sqrt{2}\mathrm{at}a=-5-4\sqrt{2}$$ $$\mathrm{local}\min =\frac{1}{2}+\sqrt{2}\mathrm{at}a=-5+4\sqrt{2}$$

Answered by mr W last updated on 08/Jan/23

$$\left(2\right)$$ $$2a+b=2$$ $$\Rightarrow 0<a<1,0<b<2$$ $$$$ $$\frac{2a^2+2a-2+4}{a+1}+\frac{b^2+b-2-2}{b+4}$$ $$=\frac{2(a^2+a+1)}{a+1}+\frac{b^2+b-4}{b+4}$$ $$=\frac{{\left(2a\right)}^2}{2a+2}+\frac{b^2-8}{b+4}+3$$ $$=\frac{{(2-b)}^2}{4-b}+\frac{b^2-8}{4+b}+3$$ $$=\frac{4(b^2-b-4)}{16-b^2}+3$$ $$=\frac{4(12-b)}{16-b^2}-1$$ $$=4\left(\underset{f\left(b\right)}{\frac{1}{4-b}+\frac{2}{4+b}}\right)-1$$ $$f^{\prime }\left(b\right)=\frac{1}{{(4-b)}^2}-\frac{2}{{(4+b)}^2}=0$$ $${(4+b)}^2-2{(4-b)}^2=0$$ $$(b-\sqrt{2}b+4+4\sqrt{2})(b+\sqrt{2}b+4-4\sqrt{2})=0$$ $$\Rightarrow b=\frac{4(\sqrt{2}-1)}{\sqrt{2}+1}=4(3-2\sqrt{2})or$$ $$\Rightarrow b=\frac{4(\sqrt{2}+1)}{\sqrt{2}-1}=4(3+2\sqrt{2})(>2,rejected)$$ $$atb=4(3-2\sqrt{2})minimum=\sqrt{2}+\frac{1}{2}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com