
Question and Answers Forum
Question Number 184738 by mnjuly1970 last updated on 11/Jan/23
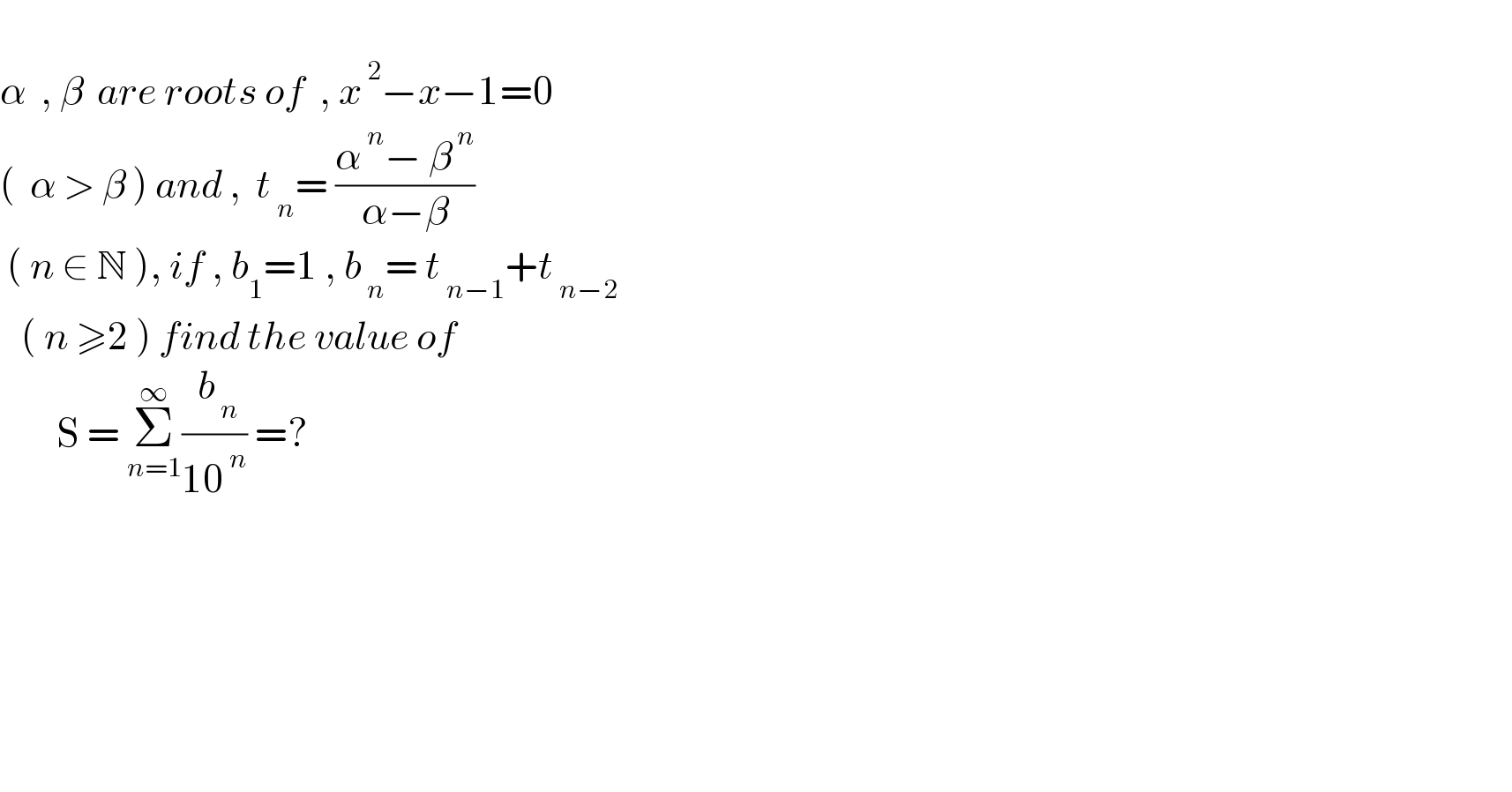
Answered by mr W last updated on 11/Jan/23
![α,β=((1±(√5))/2) α+1=α^2 β+1=β^2 α+β=1 αβ=−1 (α−β)^2 =(α+β)^2 −4αβ=5 ⇒α−β=(√5) t_n =((α^n −β^n )/(α−β))=(1/( (√5)))(α^n −β^n ) b_n =t_(n−1) +t_(n−2) =(1/( (√5)))(α^(n−1) +α^(n−2) −β^(n−1) +β^(n−2) ) =(1/( (√5)))(α^(n−2) (α+1)−β^(n−2) (β+1)) =(1/( (√5)))(α^n −β^n ) (b_n /(10^n ))=(1/( (√5)))[((α/(10)))^n −((β/(10)))^n ] S=Σ_(n=1) ^∞ (b_n /(10^n ))=(1/( (√5)))(((α/(10))/(1−(α/(10))))−((β/(10))/(1−(β/(10))))) =(1/( (√5)))((α/(10−α))−(β/(10−β))) =((10(α−β))/( (√5)(100−10(α+β)+αβ))) =((10)/(100−10−1)) =((10)/(89))](Q184763.png)
Commented bymnjuly1970 last updated on 11/Jan/23

| ||
Question and Answers Forum | ||
Question Number 184738 by mnjuly1970 last updated on 11/Jan/23 | ||
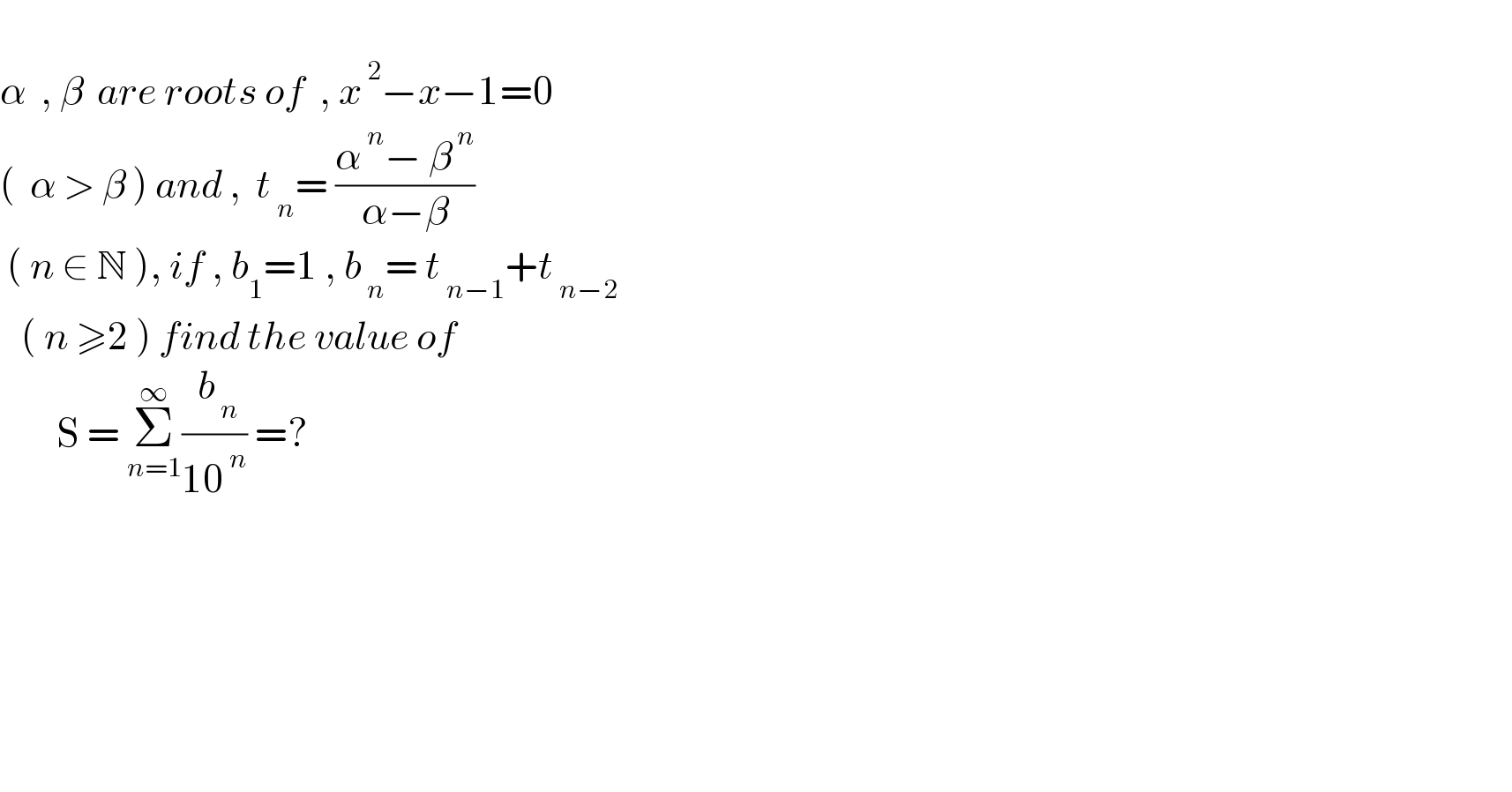 | ||
Answered by mr W last updated on 11/Jan/23 | ||
![α,β=((1±(√5))/2) α+1=α^2 β+1=β^2 α+β=1 αβ=−1 (α−β)^2 =(α+β)^2 −4αβ=5 ⇒α−β=(√5) t_n =((α^n −β^n )/(α−β))=(1/( (√5)))(α^n −β^n ) b_n =t_(n−1) +t_(n−2) =(1/( (√5)))(α^(n−1) +α^(n−2) −β^(n−1) +β^(n−2) ) =(1/( (√5)))(α^(n−2) (α+1)−β^(n−2) (β+1)) =(1/( (√5)))(α^n −β^n ) (b_n /(10^n ))=(1/( (√5)))[((α/(10)))^n −((β/(10)))^n ] S=Σ_(n=1) ^∞ (b_n /(10^n ))=(1/( (√5)))(((α/(10))/(1−(α/(10))))−((β/(10))/(1−(β/(10))))) =(1/( (√5)))((α/(10−α))−(β/(10−β))) =((10(α−β))/( (√5)(100−10(α+β)+αβ))) =((10)/(100−10−1)) =((10)/(89))](Q184763.png) | ||
| ||
Commented bymnjuly1970 last updated on 11/Jan/23 | ||
 | ||