
Question and Answers Forum
Question Number 184753 by cortano1 last updated on 11/Jan/23
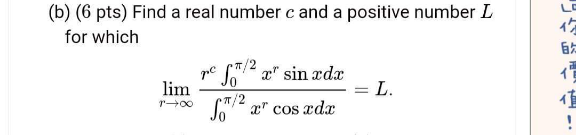
Answered by qaz last updated on 11/Jan/23

| ||
Question and Answers Forum | ||
Question Number 184753 by cortano1 last updated on 11/Jan/23 | ||
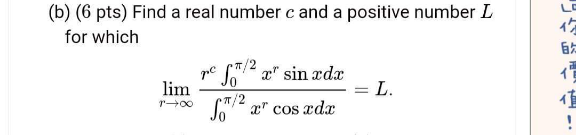 | ||
Answered by qaz last updated on 11/Jan/23 | ||
 | ||
| ||