
Question and Answers Forum
Question Number 184925 by cortano1 last updated on 14/Jan/23
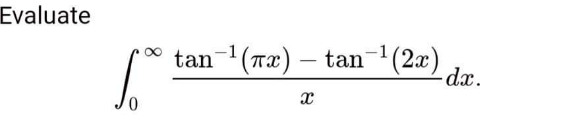
Commented by Frix last updated on 14/Jan/23
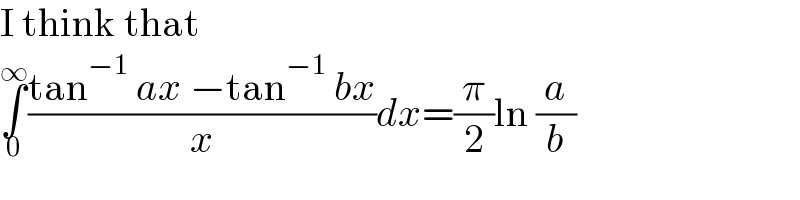
Answered by ARUNG_Brandon_MBU last updated on 14/Jan/23
![I=∫_0 ^∞ ((tan^(−1) (ax)−tan^(−1) (bx))/x)dx =∫_0 ^∞ ((tan^(−1) (ax))/x)dx−∫_0 ^∞ ((tan^(−1) (bx))/x)dx=I(a)−I(b) ⇒I ′(a)−I ′(b)=∫_0 ^∞ (dx/(1+(ax)^2 ))−∫_0 ^∞ (dx/(1+(bx)^2 )) =(1/a)[tan^(−1) (ax)]_0 ^∞ −(1/b)[tan^(−1) (bx)]_0 ^∞ =(π/(2a))−(π/(2b)) ⇒I(a)−I(b)=(π/2)lna−(π/2)lnb+C I(1)−I(1)=0=C ⇒I=I(a)−I(b)=(π/2)ln((a/b)) ∫_0 ^∞ ((tan^(−1) (πx)−tan^(−1) (2x))/x)dx=I(π)−I(2)=(π/2)ln((π/2))★](Q184930.png)
| ||
Question and Answers Forum | ||
Question Number 184925 by cortano1 last updated on 14/Jan/23 | ||
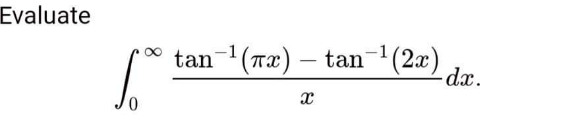 | ||
Commented by Frix last updated on 14/Jan/23 | ||
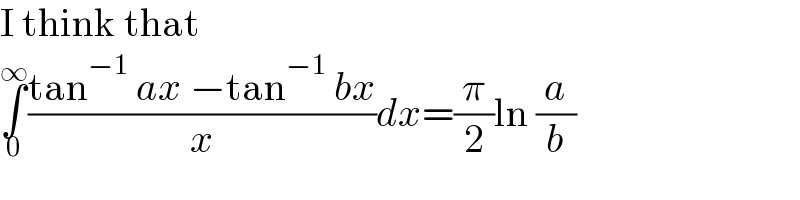 | ||
Answered by ARUNG_Brandon_MBU last updated on 14/Jan/23 | ||
![I=∫_0 ^∞ ((tan^(−1) (ax)−tan^(−1) (bx))/x)dx =∫_0 ^∞ ((tan^(−1) (ax))/x)dx−∫_0 ^∞ ((tan^(−1) (bx))/x)dx=I(a)−I(b) ⇒I ′(a)−I ′(b)=∫_0 ^∞ (dx/(1+(ax)^2 ))−∫_0 ^∞ (dx/(1+(bx)^2 )) =(1/a)[tan^(−1) (ax)]_0 ^∞ −(1/b)[tan^(−1) (bx)]_0 ^∞ =(π/(2a))−(π/(2b)) ⇒I(a)−I(b)=(π/2)lna−(π/2)lnb+C I(1)−I(1)=0=C ⇒I=I(a)−I(b)=(π/2)ln((a/b)) ∫_0 ^∞ ((tan^(−1) (πx)−tan^(−1) (2x))/x)dx=I(π)−I(2)=(π/2)ln((π/2))★](Q184930.png) | ||
| ||