Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 18498 by Tinkutara last updated on 22/Jul/17

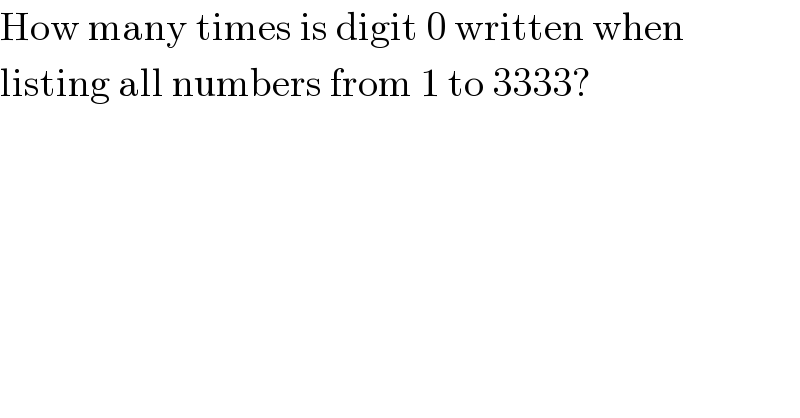
How many times is digit 0 written when listing all numbers from 1 to 3333?

$$\mathrm{How}\:\mathrm{many}\:\mathrm{times}\:\mathrm{is}\:\mathrm{digit}\:\mathrm{0}\:\mathrm{written}\:\mathrm{when} \\ $$$$\mathrm{listing}\:\mathrm{all}\:\mathrm{numbers}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{3333}? \\ $$

Commented by richard last updated on 23/Jul/17

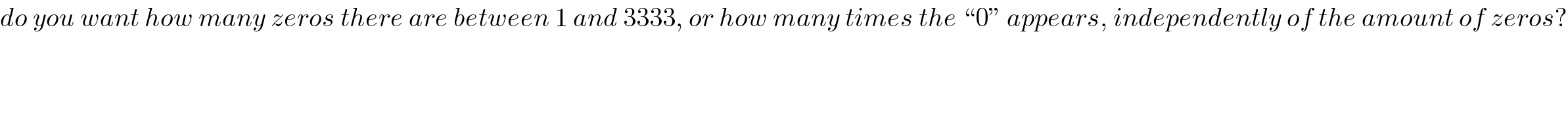
do you want how many zeros there are between 1 and 3333, or how many times the “0” appears, independently of the amount of zeros?

$${do}\:{you}\:{want}\:{how}\:{many}\:{zeros}\:{there}\:{are}\:{between}\:\mathrm{1}\:{and}\:\mathrm{3333},\:{or}\:{how}\:{many}\:{times}\:{the}\:``\mathrm{0}''\:{appears},\:{independently}\:{of}\:{the}\:{amount}\:{of}\:{zeros}? \\ $$

Answered by Abbas-Nahi last updated on 23/Jul/17

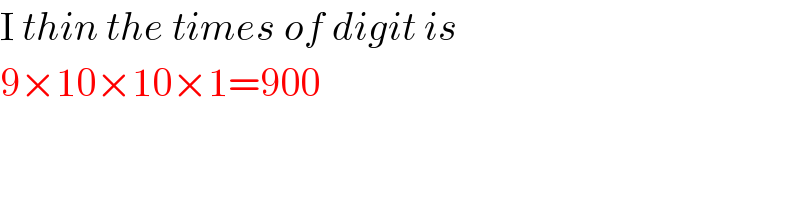
I thin the times of digit is 9×10×10×1=900

$$\mathrm{I}\:{thin}\:{the}\:{times}\:{of}\:{digit}\:{is} \\ $$$$\mathrm{9}×\mathrm{10}×\mathrm{10}×\mathrm{1}=\mathrm{900} \\ $$

Answered by richard last updated on 23/Jul/17

from 1 to 100→10 times(10,20,30...100) from 101 to 200→19 times(10 times the zero(or zeros appears) from 101 to 110 plus 9 times the zero appears from 111 to 1000) considering this padron for the hundreds to the thousands, →101 to 1000≡ 19∙9=181 times for the thousands, we could say that for 1001 to 1100= 100 times (the zero or more than one zero appears) As before, from 1100 to 2000=19∙9=181 this way, knowing this padronfor dozens, hundreds and thousands: 2000→2100=100 times 2101→3000= 181 times 3001→3100=100 times 3101→3300=19∙2= 38 times 3301→3333=10+2=12 times total: Σ=10+181+100+181+100+181+100+38+12 Σ=100∙3+181∙3+10+38+12 Σ=300+543+60 Σ=903 times ( once more, when i say “times”, i mean the number of times the zero or more than one zero appears between 1 and 3333)

$${from}\:\mathrm{1}\:{to}\:\mathrm{100}\rightarrow\mathrm{10}\:{times}\left(\mathrm{10},\mathrm{20},\mathrm{30}...\mathrm{100}\right) \\ $$$${from}\:\mathrm{101}\:{to}\:\mathrm{200}\rightarrow\mathrm{19}\:{times}\left(\mathrm{10}\:{times}\:{the}\:{zero}\left({or}\:{zeros}\:{appears}\right)\:{from}\:\mathrm{101}\:{to}\:\mathrm{110}\:{plus}\:\mathrm{9}\:{times}\:{the}\:{zero}\:{appears}\:{from}\:\mathrm{111}\:{to}\:\mathrm{1000}\right) \\ $$$${considering}\:{this}\:{padron}\:{for}\:{the}\:{hundreds}\:{to}\:{the}\:{thousands}, \\ $$$$\rightarrow\mathrm{101}\:{to}\:\mathrm{1000}\equiv\:\mathrm{19}\centerdot\mathrm{9}=\mathrm{181}\:{times} \\ $$$${for}\:{the}\:{thousands},\:{we}\:{could}\:{say}\:{that}\:{for}\:\mathrm{1001}\:{to}\:\mathrm{1100}=\:\mathrm{100}\:{times}\:\left({the}\:{zero}\:{or}\:{more}\:{than}\:{one}\:{zero}\:{appears}\right) \\ $$$${As}\:{before},\:{from}\:\mathrm{1100}\:{to}\:\mathrm{2000}=\mathrm{19}\centerdot\mathrm{9}=\mathrm{181} \\ $$$${this}\:{way},\:{knowing}\:{this}\:{padronfor} \\ $$$${dozens},\:{hundreds}\:{and}\:{thousands}: \\ $$$$\mathrm{2000}\rightarrow\mathrm{2100}=\mathrm{100}\:{times} \\ $$$$\mathrm{2101}\rightarrow\mathrm{3000}=\:\mathrm{181}\:{times} \\ $$$$\mathrm{3001}\rightarrow\mathrm{3100}=\mathrm{100}\:{times} \\ $$$$\mathrm{3101}\rightarrow\mathrm{3300}=\mathrm{19}\centerdot\mathrm{2}=\:\mathrm{38}\:{times} \\ $$$$\mathrm{3301}\rightarrow\mathrm{3333}=\mathrm{10}+\mathrm{2}=\mathrm{12}\:{times} \\ $$$${total}: \\ $$$$\Sigma=\mathrm{10}+\mathrm{181}+\mathrm{100}+\mathrm{181}+\mathrm{100}+\mathrm{181}+\mathrm{100}+\mathrm{38}+\mathrm{12} \\ $$$$\Sigma=\mathrm{100}\centerdot\mathrm{3}+\mathrm{181}\centerdot\mathrm{3}+\mathrm{10}+\mathrm{38}+\mathrm{12} \\ $$$$\Sigma=\mathrm{300}+\mathrm{543}+\mathrm{60} \\ $$$$\Sigma=\mathrm{903}\:{times}\:\left(\:{once}\:{more},\:{when}\:{i}\:{say}\:``{times}'',\:{i}\:{mean}\:{the}\:{number}\:{of}\:{times}\:{the}\:{zero}\:{or}\:{more}\:{than}\:{one}\:{zero}\:{appears}\:{between}\:\mathrm{1}\:{and}\:\mathrm{3333}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mrW1 last updated on 23/Jul/17

from 1 to 100→11 zeros(10,20,30...100)

$${from}\:\mathrm{1}\:{to}\:\mathrm{100}\rightarrow\mathrm{11}\:{zeros}\left(\mathrm{10},\mathrm{20},\mathrm{30}...\mathrm{100}\right) \\ $$$$ \\ $$

Commented by richard last updated on 23/Jul/17

why 11? the question asks about how many times the zero appears, not how many zeros exists between then, is it not?

$${why}\:\mathrm{11}?\:{the}\:{question}\:{asks}\:{about}\:{how}\:{many}\:{times}\:{the}\:{zero}\:{appears},\:{not}\:{how}\:{many}\:{zeros}\:{exists}\:{between}\:{then},\:{is}\:{it}\:{not}? \\ $$

Commented by richard last updated on 23/Jul/17

I need to fix it, thd correct answer is Σ=903 times It means the zero(or more zeros)r appears 903 times between 1 and 3333, not how many zeros are between 1 and 3333

$${I}\:{need}\:{to}\:{fix}\:{it},\:{thd}\:{correct}\:{answer}\:{is} \\ $$$$\Sigma=\mathrm{903}\:{times} \\ $$$${It}\:{means}\:{the}\:{zero}\left({or}\:{more}\:{zeros}\right){r}\:{appears}\:\mathrm{903}\:{times}\:{between}\:\mathrm{1}\:{and}\:\mathrm{3333},\:{not}\:{how}\:{many}\:{zeros}\:{are}\:{between}\:\mathrm{1}\:{and}\:\mathrm{3333} \\ $$

Commented by richard last updated on 23/Jul/17

the∗

$${the}\ast \\ $$

Commented by richard last updated on 23/Jul/17

It should be Σ=903 times, not Σ=903 zeros, sorry :)

$$\left.{It}\:{should}\:{be}\:\Sigma=\mathrm{903}\:{times},\:{not}\:\Sigma=\mathrm{903}\:{zeros},\:{sorry}\::\right) \\ $$

Commented by mrW1 last updated on 23/Jul/17

the question asks how many times “0” is written. i understand for example in the number 200 zero is written 2 times, not one time.

$$\mathrm{the}\:\mathrm{question}\:\mathrm{asks}\:\mathrm{how}\:\mathrm{many}\:\mathrm{times}\:``\mathrm{0}'' \\ $$$$\mathrm{is}\:\mathrm{written}.\:\mathrm{i}\:\mathrm{understand}\:\mathrm{for}\:\mathrm{example} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{number}\:\mathrm{200}\:\mathrm{zero}\:\mathrm{is}\:\mathrm{written}\:\mathrm{2}\:\mathrm{times}, \\ $$$$\mathrm{not}\:\mathrm{one}\:\mathrm{time}. \\ $$

Commented by Abbas-Nahi last updated on 23/Jul/17

it solve by (counting method m×n)

$${it}\:{solve}\:{by}\:\left({counting}\:{method}\:\:{m}×{n}\right) \\ $$

Commented by richard last updated on 23/Jul/17

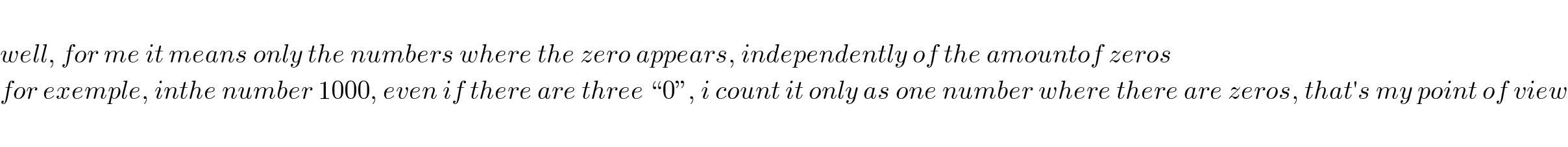
well, for me it means only the numbers where the zero appears, independently of the amountof zeros for exemple, inthe number 1000, even if there are three “0”, i count it only as one number where there are zeros, that′s my point of view

$$ \\ $$$${well},\:{for}\:{me}\:{it}\:{means}\:{only}\:{the}\:{numbers}\:{where}\:{the}\:{zero}\:{appears},\:{independently}\:{of}\:{the}\:{amountof}\:{zeros} \\ $$$${for}\:{exemple},\:{inthe}\:{number}\:\mathrm{1000},\:{even}\:{if}\:{there}\:{are}\:{three}\:``\mathrm{0}'',\:{i}\:{count}\:{it}\:{only}\:{as}\:{one}\:{number}\:{where}\:{there}\:{are}\:{zeros},\:{that}'{s}\:{my}\:{point}\:{of}\:{view} \\ $$$$ \\ $$

Answered by richard last updated on 22/Jul/17

from 1 to 100→10 zeros(10,20,30...100) from 101 to 200→19 zeros(10 zeros from 101 to 110 plus 9 zeros from 111 to +100200) considering this padron for the hundreds to the thousands, →101 to 1000≡ 19∙9=181 zeros for the thousands, we could say that 1001 to 1100= 100 zeros(1001 to 1100) As before, from 1100 to 2000=19∙9=181 this way, knowing this padronfor dozens, hundreds and thousands: 2000→2100=100 zeros 2101→3000= 181 zeros 3001→3100=100 zeros 3101→3300=19∙2= 38 zeros 3301→3333=10+2=12 zeros total: Σ=10+181+100+181+100+181+100+38+12 Σ=100∙3+181∙3+10+38+12 Σ=300+543+60 Σ=903 zeros

$${from}\:\mathrm{1}\:{to}\:\mathrm{100}\rightarrow\mathrm{10}\:{zeros}\left(\mathrm{10},\mathrm{20},\mathrm{30}...\mathrm{100}\right) \\ $$$${from}\:\mathrm{101}\:{to}\:\mathrm{200}\rightarrow\mathrm{19}\:{zeros}\left(\mathrm{10}\:{zeros}\:{from}\:\mathrm{101}\:{to}\:\mathrm{110}\:{plus}\:\mathrm{9}\:{zeros}\:{from}\:\mathrm{111}\:{to}\:+\mathrm{100200}\right) \\ $$$${considering}\:{this}\:{padron}\:{for}\:{the}\:{hundreds}\:{to}\:{the}\:{thousands}, \\ $$$$\rightarrow\mathrm{101}\:{to}\:\mathrm{1000}\equiv\:\mathrm{19}\centerdot\mathrm{9}=\mathrm{181}\:{zeros} \\ $$$${for}\:{the}\:{thousands},\:{we}\:{could}\:{say}\:{that}\:\mathrm{1001}\:{to}\:\mathrm{1100}=\:\mathrm{100}\:{zeros}\left(\mathrm{1001}\:{to}\:\mathrm{1100}\right) \\ $$$${As}\:{before},\:{from}\:\mathrm{1100}\:{to}\:\mathrm{2000}=\mathrm{19}\centerdot\mathrm{9}=\mathrm{181} \\ $$$${this}\:{way},\:{knowing}\:{this}\:{padronfor} \\ $$$${dozens},\:{hundreds}\:{and}\:{thousands}: \\ $$$$\mathrm{2000}\rightarrow\mathrm{2100}=\mathrm{100}\:{zeros} \\ $$$$\mathrm{2101}\rightarrow\mathrm{3000}=\:\mathrm{181}\:{zeros} \\ $$$$\mathrm{3001}\rightarrow\mathrm{3100}=\mathrm{100}\:{zeros} \\ $$$$\mathrm{3101}\rightarrow\mathrm{3300}=\mathrm{19}\centerdot\mathrm{2}=\:\mathrm{38}\:{zeros} \\ $$$$\mathrm{3301}\rightarrow\mathrm{3333}=\mathrm{10}+\mathrm{2}=\mathrm{12}\:{zeros} \\ $$$${total}: \\ $$$$\Sigma=\mathrm{10}+\mathrm{181}+\mathrm{100}+\mathrm{181}+\mathrm{100}+\mathrm{181}+\mathrm{100}+\mathrm{38}+\mathrm{12} \\ $$$$\Sigma=\mathrm{100}\centerdot\mathrm{3}+\mathrm{181}\centerdot\mathrm{3}+\mathrm{10}+\mathrm{38}+\mathrm{12} \\ $$$$\Sigma=\mathrm{300}+\mathrm{543}+\mathrm{60} \\ $$$$\Sigma=\mathrm{903}\:{zeros} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by Abbas-Nahi last updated on 23/Jul/17

Answered by mrW1 last updated on 24/Jul/17

N=number of numbers in which zero(s) occurs Z=number of zero(s) in the numbers X∈[1,9] Y∈[1,3] W∈[1,2] (1) numbers with 1 digit: X N=0 Z=0 (2) numbers with 2 digits: X0 N=9 Z=9 (3) numbers with 3 digits: (3.1) X0X, XX0 N=2×9×9=162 Z=162 (3.2) X00 N=9 Z=9×2=18 (4) numbers with 4 digits: (4.1) W0XX, WX0X, WXX0 N=3×2×9×9=486 Z=486 (4.2) W00X, W0X0, WX00 N=3×2×9=54 Z=54×2=108 (4.3) W000 N=2 Z=2×3=6 (4.4) 30XX, 3Y0X, 3WX0, 33Y0 N=9×9+3×9+2×9+3=129 Z=129 (4.5) 300X, 3Y00, 30X0 N=9+3+9=21 Z=21×2=42 (4.6) 3000 N=1 Z=3 ΣN=9+162+9+486+54+2+129+21+1=873 ΣZ=9+162+18+486+108+6+129+42+3=963 i.e. there are 873 numbers in which “0” occurs. in them “0” is written 963 times.

$$\mathrm{N}=\mathrm{number}\:\mathrm{of}\:\mathrm{numbers}\:\mathrm{in}\:\mathrm{which}\:\mathrm{zero}\left(\mathrm{s}\right)\:\mathrm{occurs} \\ $$$$\mathrm{Z}=\mathrm{number}\:\mathrm{of}\:\mathrm{zero}\left(\mathrm{s}\right)\:\mathrm{in}\:\mathrm{the}\:\mathrm{numbers} \\ $$$$\mathrm{X}\in\left[\mathrm{1},\mathrm{9}\right] \\ $$$$\mathrm{Y}\in\left[\mathrm{1},\mathrm{3}\right] \\ $$$$\mathrm{W}\in\left[\mathrm{1},\mathrm{2}\right] \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{1}\:\mathrm{digit}:\:\mathrm{X} \\ $$$$\mathrm{N}=\mathrm{0} \\ $$$$\mathrm{Z}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{2}\:\mathrm{digits}:\:\mathrm{X0} \\ $$$$\mathrm{N}=\mathrm{9} \\ $$$$\mathrm{Z}=\mathrm{9} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{3}\:\mathrm{digits}:\: \\ $$$$\left(\mathrm{3}.\mathrm{1}\right)\:\mathrm{X0X},\:\mathrm{XX0} \\ $$$$\mathrm{N}=\mathrm{2}×\mathrm{9}×\mathrm{9}=\mathrm{162} \\ $$$$\mathrm{Z}=\mathrm{162} \\ $$$$\left(\mathrm{3}.\mathrm{2}\right)\:\mathrm{X00} \\ $$$$\mathrm{N}=\mathrm{9} \\ $$$$\mathrm{Z}=\mathrm{9}×\mathrm{2}=\mathrm{18} \\ $$$$ \\ $$$$\left(\mathrm{4}\right)\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{4}\:\mathrm{digits}:\: \\ $$$$\left(\mathrm{4}.\mathrm{1}\right)\:\mathrm{W0XX},\:\mathrm{WX0X},\:\mathrm{WXX0} \\ $$$$\mathrm{N}=\mathrm{3}×\mathrm{2}×\mathrm{9}×\mathrm{9}=\mathrm{486} \\ $$$$\mathrm{Z}=\mathrm{486} \\ $$$$\left(\mathrm{4}.\mathrm{2}\right)\:\mathrm{W00X},\:\mathrm{W0X0},\:\mathrm{WX00} \\ $$$$\mathrm{N}=\mathrm{3}×\mathrm{2}×\mathrm{9}=\mathrm{54} \\ $$$$\mathrm{Z}=\mathrm{54}×\mathrm{2}=\mathrm{108} \\ $$$$\left(\mathrm{4}.\mathrm{3}\right)\:\mathrm{W000} \\ $$$$\mathrm{N}=\mathrm{2} \\ $$$$\mathrm{Z}=\mathrm{2}×\mathrm{3}=\mathrm{6} \\ $$$$\left(\mathrm{4}.\mathrm{4}\right)\:\mathrm{30XX},\:\mathrm{3Y0X},\:\mathrm{3WX0},\:\mathrm{33Y0} \\ $$$$\mathrm{N}=\mathrm{9}×\mathrm{9}+\mathrm{3}×\mathrm{9}+\mathrm{2}×\mathrm{9}+\mathrm{3}=\mathrm{129} \\ $$$$\mathrm{Z}=\mathrm{129} \\ $$$$\left(\mathrm{4}.\mathrm{5}\right)\:\mathrm{300X},\:\mathrm{3Y00},\:\mathrm{30X0} \\ $$$$\mathrm{N}=\mathrm{9}+\mathrm{3}+\mathrm{9}=\mathrm{21} \\ $$$$\mathrm{Z}=\mathrm{21}×\mathrm{2}=\mathrm{42} \\ $$$$\left(\mathrm{4}.\mathrm{6}\right)\:\mathrm{3000} \\ $$$$\mathrm{N}=\mathrm{1} \\ $$$$\mathrm{Z}=\mathrm{3} \\ $$$$ \\ $$$$\Sigma\mathrm{N}=\mathrm{9}+\mathrm{162}+\mathrm{9}+\mathrm{486}+\mathrm{54}+\mathrm{2}+\mathrm{129}+\mathrm{21}+\mathrm{1}=\mathrm{873} \\ $$$$\Sigma\mathrm{Z}=\mathrm{9}+\mathrm{162}+\mathrm{18}+\mathrm{486}+\mathrm{108}+\mathrm{6}+\mathrm{129}+\mathrm{42}+\mathrm{3}=\mathrm{963} \\ $$$$ \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{there}\:\mathrm{are}\:\mathrm{873}\:\mathrm{numbers}\:\mathrm{in}\:\mathrm{which}\:``\mathrm{0}''\:\mathrm{occurs}. \\ $$$$\mathrm{in}\:\mathrm{them}\:``\mathrm{0}''\:\mathrm{is}\:\mathrm{written}\:\mathrm{963}\:\mathrm{times}. \\ $$

Commented by Tinkutara last updated on 24/Jul/17

Thanks Sir! Amazing!

$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{Amazing}! \\ $$

Commented by mrW1 last updated on 24/Jul/17

Thank you sir for checking!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{checking}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com