
Question Number 184992 by SANOGO last updated on 15/Jan/23
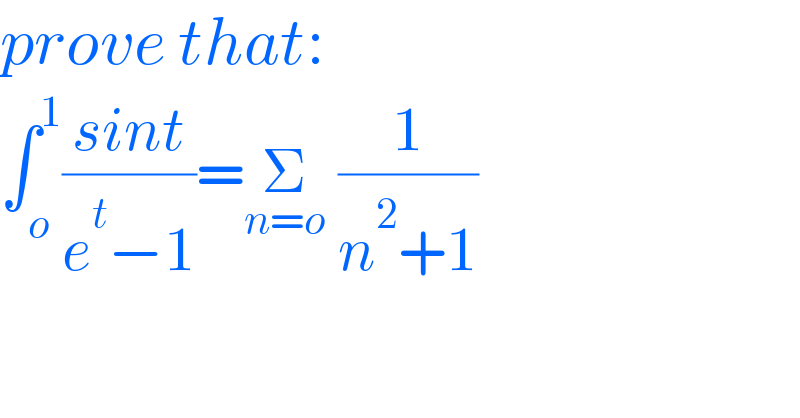
$${prove}\:{that}: \\ $$$$\int_{{o}} ^{\mathrm{1}} \frac{{sint}}{{e}^{{t}} −\mathrm{1}}=\underset{{n}={o}} {\sum}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 15/Jan/23
![∫_0 ^∞ ((sint)/(e^t −1))dt=∫_0 ^∞ ((e^(−t) sint)/(1−e^(−t) ))dt =∫_0 ^∞ (e^(−t) sintΣ_(n=0) ^∞ e^(−nt) )dt=Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)t) sintdt =Σ_(n=0) ^∞ [(e^(−(n+1)t) /((n+1)^2 +1))(−(n+1)sint−cost)]_0 ^∞ =Σ_(n=0) ^∞ (1/((n+1)^2 +1))=Σ_(n=1) ^∞ (1/(n^2 +1))=(π/2)cothπ−(1/2)](Q185001.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{t}}{{e}^{{t}} −\mathrm{1}}{dt}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} \mathrm{sin}{t}}{\mathrm{1}−{e}^{−{t}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left({e}^{−{t}} \mathrm{sin}{t}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−{nt}} \right){dt}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}+\mathrm{1}\right){t}} \mathrm{sin}{tdt} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{e}^{−\left({n}+\mathrm{1}\right){t}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\left(−\left({n}+\mathrm{1}\right)\mathrm{sin}{t}−\mathrm{cos}{t}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\frac{\pi}{\mathrm{2}}\mathrm{coth}\pi−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by SANOGO last updated on 15/Jan/23

$${merci}\:{bien} \\ $$
