
Question and Answers Forum
Question Number 185013 by Shrinava last updated on 15/Jan/23

Commented by a.lgnaoui last updated on 16/Jan/23

Commented by Shrinava last updated on 16/Jan/23
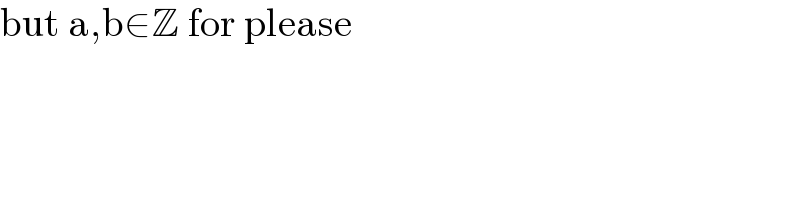
Commented by Shrinava last updated on 16/Jan/23
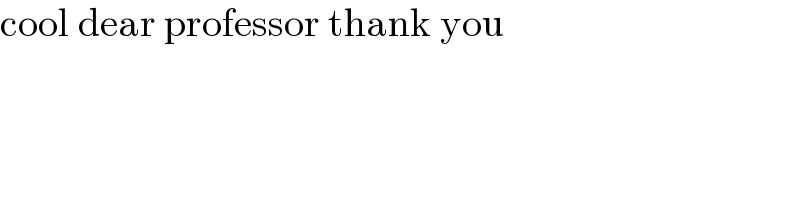
Answered by a.lgnaoui last updated on 16/Jan/23
![A= (a^2 −2b^2 ) 9A=(9a^2 −18b^2 ) 6A^2 =6 (a^2 −2b^2 )^2 ; A^3 =(a^2 −2b^2 )^3 27I_2 =27 A^3 −6A^2 +9A−27=0 A=5,2646329 a^2 −2b^2 =5,2646329 a^2 =2b^2 +5,264633 a^6 −8b^6 −3(2a^2 b^2 (a^2 −2b^2 )−6(a^4 +4b^4 −4a^2 b^2 )+9(a^2 −2b^2 )−27=0 a^6 −(a^2 −x_0 )^3 −6a^2 ×(((a^2 −x_0 )/2))x_0 −6[a^4 +4(((a^2 −x_0 ))/2))(((a^2 −x_0 ))/2)−a^2 )]+9x_0 −27=0 a^6 −(a^2 −x_0 )^3 −a^2 x_0 (a^2 −x_0 )−6(a^2 −x_0 )(((a^2 −x_0 )/2)−a^2 )+9x_0 −27=0 =3a^4 x_0 −3a^2 x_0 ^2 +x_0 ^3 −(a^2 −x_0 )[a^2 x_0 +3(a^2 −x_0 )−6a^2 )]+9x_0 −27=0 =3a^2 x_0 (a^2 −x_0 )+x_0 ^3 −(a^2 −x_0 )[a^2 (x_0 −3)−3x_0 ]+9x_0 −27=0 (a^2 −x_0 )[3a^2 x_0 −a^2 (x_0 −3)−3x_0 ]+x_0 ^3 +9x_0 −27=0 (a^2 −x_0 )[a^2 (2x_0 −3)−3x_0 ]+x_0 ^3 +9(x_0 −3)=0 (a^2 −x_0 )[2x_0 (a^2 −x_0 )−3(a^2 −x_0 )+2x_0 ^2 −6x_0 ]+x_0 ^3 +9(x_0 −3) a^2 −x_0 =z x_0 −3=y_0 z(2x_0 z−3+2x_0 y_0 )]+(y_0 +3)^3 +9y_0 2x_0 z^2 +(2x_0 y_0 −3)z+(y_0 +3)^2 +9y_0 =0 z^2 +(y_0 −(3/(2x_0 ))−(3/(2x_0 )))z+(y_0 +3)^2 +9y_0 =0 (z+((x_0 y_0 −3)/2))^2 −(((x_0 y_0 −3)^2 )/4)+x_0 ^3 +9y_0 =0 x_0 y_0 =5,264633×2,264633=11,922461 2x_0 = y_0 =2,264633 (z+((8,922461)/2))^2 −(((8,922461)^2 )/4)+253,218 (z+4,46123)^2 −273,12057 (z+4,46123−(√(273,12057)) )=0 z=16,52636−4,46123=12,065129 a^2 −x_0 =12,065129 a^2 =12,065129+5,264633 =17,329762 a=4,163.. ; b=2,277](Q185035.png)
Commented by aba last updated on 16/Jan/23

Commented by aba last updated on 16/Jan/23

Commented by aba last updated on 16/Jan/23
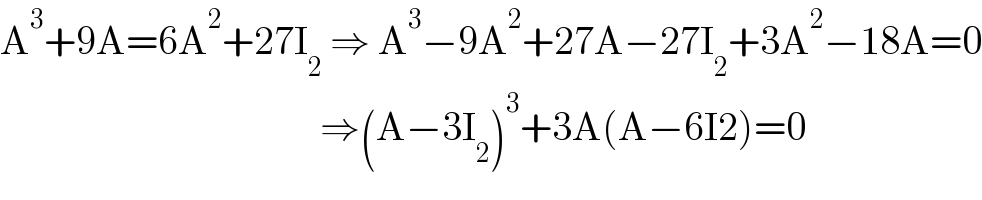
Commented by a.lgnaoui last updated on 16/Jan/23
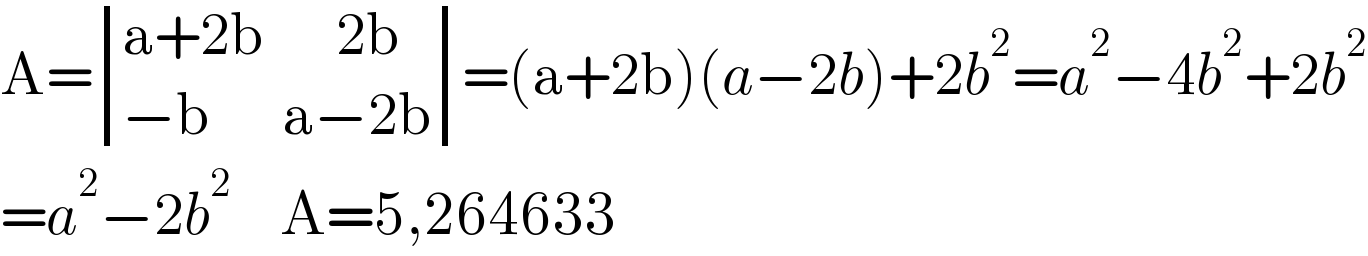
Commented by Frix last updated on 16/Jan/23
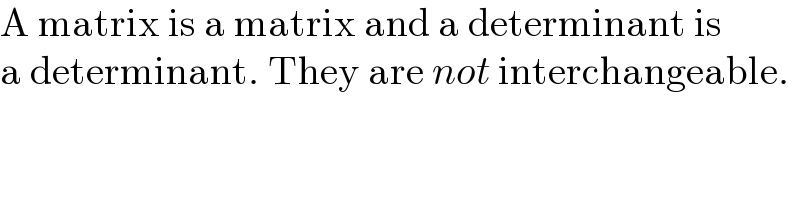
Answered by Frix last updated on 16/Jan/23
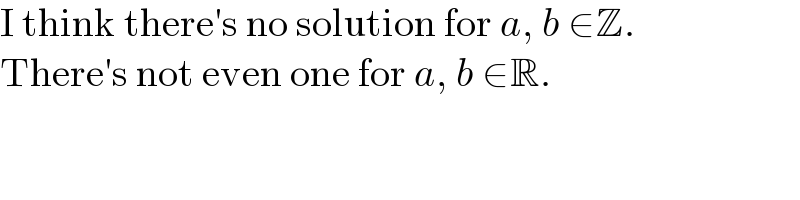
Answered by aleks041103 last updated on 17/Jan/23
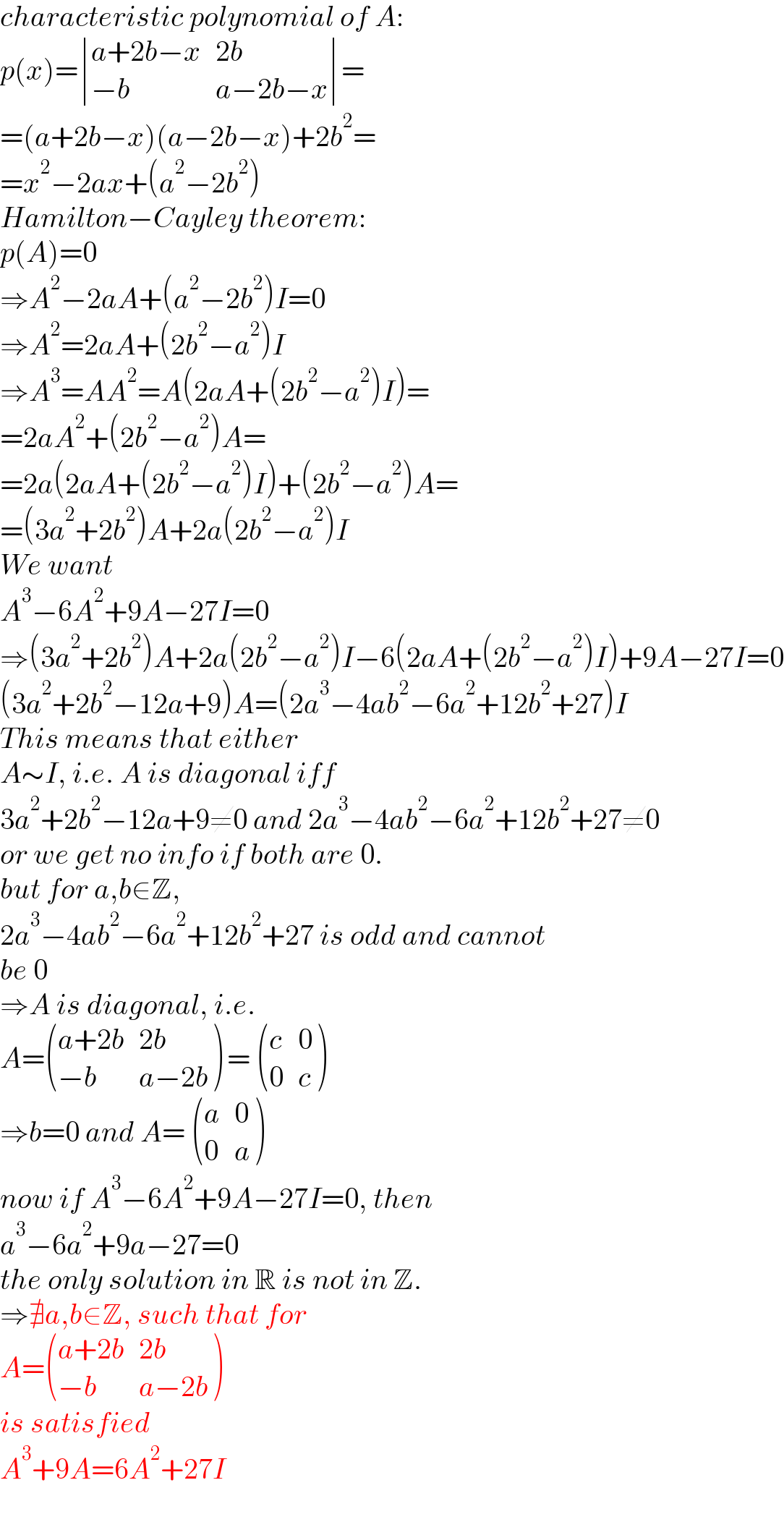
Commented by Frix last updated on 17/Jan/23

Commented by Shrinava last updated on 20/Jan/23
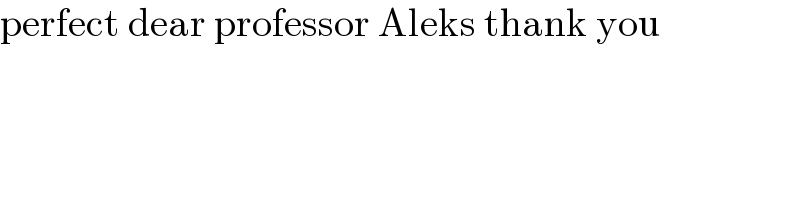
Answered by Frix last updated on 17/Jan/23
![Just to complete it: A^3 −6A^2 +9A−27I_2 = [((term_1 ),(term_2 )),((term_3 ),(term_4 )) ] All terms =0 (1) a^3 +6a^2 b+6ab^2 +4b^3 −6a^2 −24ab−12b^2 +9a+18b−27=0 (2) 6a^2 b+4b^3 −24ab+18b=0 (3) −3a^2 b−2b^3 +12ab−9b=0 (4) a^3 −6a^2 b+6ab^2 −4b^3 −6a^2 +24ab−12b^2 +9a−18b−27=0 From (2) or (3) we get a=2+((√(3−2b^2 ))/( (√3)))s with s=±1 From (1) or (4) we get ((2(8b^2 −3)(√(9−6b^2 )))/9)s−25=0 We get s=−1∧b≈±1.58009i∧a≈.367684 s=+1∧b≈±(1.73133±.790045i)∧a≈2.81616±1.11729i](Q185102.png)
