
Question and Answers Forum
Question Number 185085 by Ml last updated on 16/Jan/23

Answered by Frix last updated on 16/Jan/23
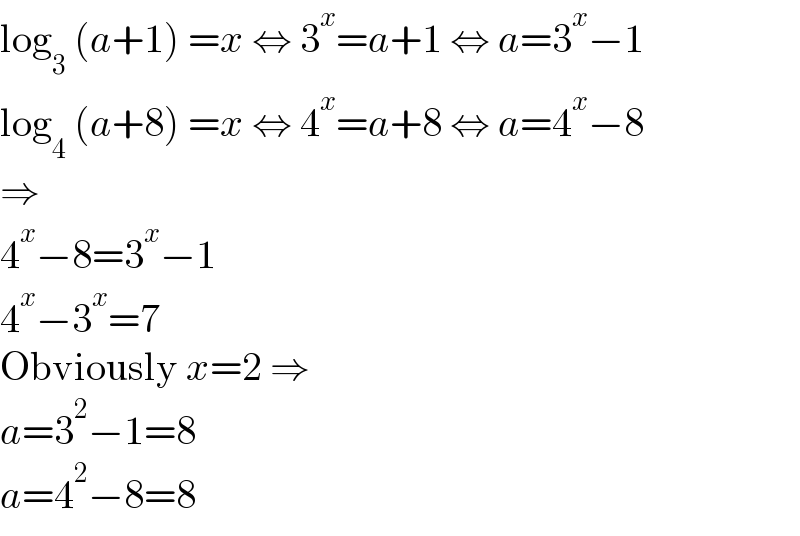
Answered by aba last updated on 16/Jan/23
![consider the function f(x)=log_3 (x+1)−log_4 (x+8) Df=]−1,+∞[ f^′ (x)=(1/((x+1)ln(3)))−(1/((x+8)ln(4))) =(((x+8)ln(4)−(x+1)ln(3))/((x+1)(x+8)ln(3)ln(4))) =((x(ln(4)−ln(3))+8ln(4)−ln(3))/((x+1)(x+8)ln(3)ln(4))) the denominator is positive on the domain of f f′(x)=0 ⇒ x(ln(4)−ln(3))+8ln(4)−ln(3)=0 ⇒ x=−((8ln(4)−ln(3))/(ln(4)−ln(3))) ⇒x=−((ln((4^8 /3)))/(ln((4/3)))) <−1 ⇒x<−1 so the function f is strictly increasing on ]−1,+∞[. Hence the equation f(x)=0 has at most one solution since f(8)=0, we found it](Q185092.png)
| ||
Question and Answers Forum | ||
Question Number 185085 by Ml last updated on 16/Jan/23 | ||
 | ||
Answered by Frix last updated on 16/Jan/23 | ||
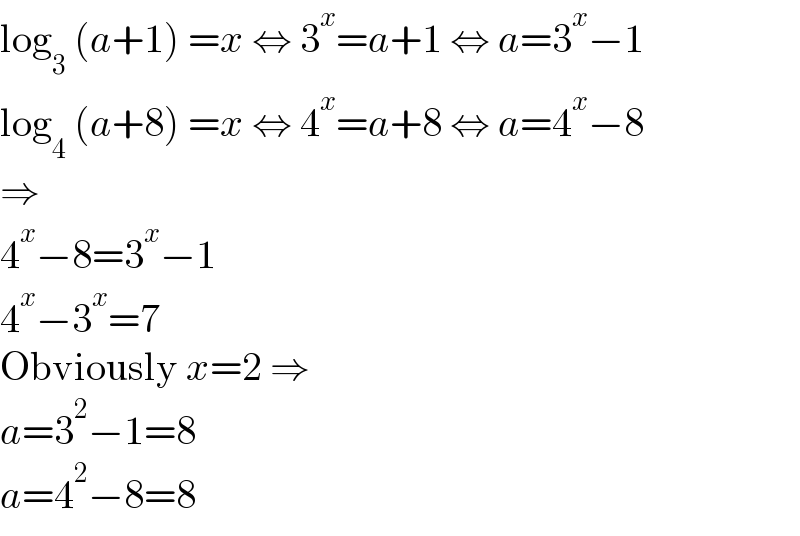 | ||
| ||
Answered by aba last updated on 16/Jan/23 | ||
![consider the function f(x)=log_3 (x+1)−log_4 (x+8) Df=]−1,+∞[ f^′ (x)=(1/((x+1)ln(3)))−(1/((x+8)ln(4))) =(((x+8)ln(4)−(x+1)ln(3))/((x+1)(x+8)ln(3)ln(4))) =((x(ln(4)−ln(3))+8ln(4)−ln(3))/((x+1)(x+8)ln(3)ln(4))) the denominator is positive on the domain of f f′(x)=0 ⇒ x(ln(4)−ln(3))+8ln(4)−ln(3)=0 ⇒ x=−((8ln(4)−ln(3))/(ln(4)−ln(3))) ⇒x=−((ln((4^8 /3)))/(ln((4/3)))) <−1 ⇒x<−1 so the function f is strictly increasing on ]−1,+∞[. Hence the equation f(x)=0 has at most one solution since f(8)=0, we found it](Q185092.png) | ||
| ||