Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 185137 by emmanuelson123 last updated on 17/Jan/23

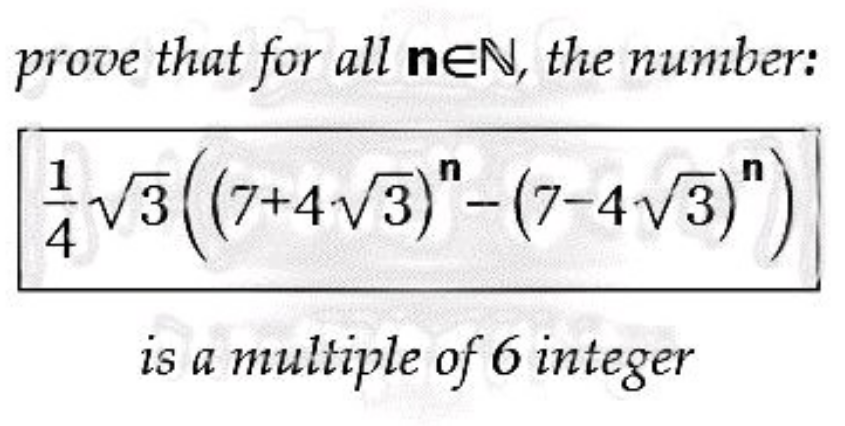
Answered by CElcedricjunior last updated on 17/Jan/23

$$\mathit{m}\mathit{o}\mathit{n}\mathit{t}\mathit{r}\mathit{o}\mathit{n}\mathit{s}\mathit{q}\mathit{u}\mathit{e}\mathrm{\forall }\mathit{n}\in \mathit{I}\mathit{N}$$$$\frac{\sqrt{3}}{4}[{(7+4\sqrt{3})}^{\mathit{n}}-{(7-4\sqrt{3})}^{\mathit{n}}]\equiv 0\left[6\right]$$$$\mathit{p}\mathit{o}\mathit{s}\mathit{o}\mathit{n}\mathit{s}\mathit{p}\left(\mathit{n}\right)=\frac{\sqrt{3}}{4}[{(7+4\sqrt{3})}^{\mathit{n}}-{(7-4\sqrt{3})}^{\mathit{n}}]$$$$\ast \mathit{p}\mathit{o}\mathit{u}\mathit{r}\mathit{n}=0\mathit{o}\mathit{n}\mathit{a}$$$$\frac{\sqrt{3}}{4}[{(7+4\sqrt{3})}^0-{(7-4\sqrt{3})}^0]=\frac{\sqrt{3}}{4}(1-1)=0\equiv 0\left[6\right]$$$${\mathit{D}}^{\prime }\mathit{o}\stackrel{`}{\mathit{u}}p\left(0\right)\mathit{v}\mathit{r}\mathit{a}\mathit{i}$$$$\ast \mathit{p}\mathit{o}\mathit{u}\mathit{r}\mathit{n}⩾0\mathit{s}\mathit{u}\mathit{p}\mathit{p}\mathit{o}\mathit{s}\mathit{o}\mathit{n}\mathit{s}\mathit{p}\left(\mathit{n}\right)\mathit{v}\mathit{r}\mathit{a}\mathit{i}\mathit{e}\mathit{e}\mathit{t}\mathit{m}\mathit{o}\mathit{n}\mathit{t}\mathit{r}\mathit{o}\mathit{n}\mathit{s}\mathit{q}\mathit{u}\mathit{e}\mathit{p}(\mathit{n}+1){\mathit{l}}^{\prime }\mathit{e}\mathit{s}\mathit{t}\mathit{a}\mathit{u}\mathit{s}\mathit{s}\mathit{i}$$$$\mathit{a}\mathit{u}\mathit{r}\mathit{a}\mathit{n}\mathit{g}(\mathit{n}+1)\mathit{o}\mathit{n}\mathit{a}$$$$\frac{\sqrt{3}}{4}[{(7+4\sqrt{3})}^{\mathit{n}}-{(7-4\sqrt{3})}^{\mathit{n}}]\equiv 0\left[6\right]$$$$=>\frac{\sqrt{3}{(7+4\sqrt{3})}^n}{4}\equiv \frac{\sqrt{3}}{4}{(7-4\sqrt{3})}^{\mathit{n}}\left[6\right]$$$$=>{(7+4\sqrt{3})}^{\mathit{n}}\equiv {(7-4\sqrt{3})}^{\mathit{n}}\left[6\right]$$$$=>{(7+4\sqrt{3})}^{\mathit{n}+1}\equiv {(7-4\sqrt{3})}^{\mathit{n}-1}\left[6\right]$$$$=>{(7+4\sqrt{3})}^{\mathit{n}+1}-{(7-4\sqrt{3})}^{\mathit{n}-1}\equiv 0\left[6\right]$$$$=>\frac{\sqrt{3}}{4}[{(7+4\sqrt{3})}^{\mathit{n}+1}-{(7-4\sqrt{3})}^{\mathit{n}+1}]\equiv 0\left[6\right]\mathit{c}\mathit{a}\mathit{s}{(7-4\sqrt{3})}^{\mathit{n}-1}⩽{(7-4\sqrt{3})}^{\mathit{n}+1}$$$${\mathit{d}}^{\prime }\mathit{o}\stackrel{`}{\mathit{u}}\mathit{p}(\mathit{n}+1)\mathit{v}\mathit{r}\mathit{a}\mathit{i}\mathit{e}$$$$\mathit{d}\mathit{o}\mathit{n}\mathit{c}\mathrm{\forall }\mathit{n}\in \mathit{I}\mathit{N}$$$$\text{Missing left or extra right}$$$$$$$$$$

Commented by aba last updated on 17/Jan/23

$$\mathrm{proof}\mathrm{by}\mathrm{recurence}?$$

Answered by JDamian last updated on 17/Jan/23

$$S_n=\sqrt{3}[{(7+4\sqrt{3})}^n-{(7-4\sqrt{3})}^n]=$$$$=\sqrt{3}\mathrm{\Sigma }[C_{n,k}\cdot (7^{n-k}\cdot {\left(4\sqrt{3}\right)}^k]1⩽k⩽nk=2p+1$$$$S_n=\mathrm{\Sigma }[C_{n,k}\cdot (7^{n-k}\cdot \sqrt{3}\cdot {\left(4\sqrt{3}\right)}^k]$$$$$$$$\sqrt{3}\cdot {\left(4\sqrt{3}\right)}^k=\sqrt{3}\cdot {\left(4\sqrt{3}\right)}^{2p+1}=$$$$=\sqrt{3}\cdot {\left[{\left(4\sqrt{3}\right)}^2\right]}^p\cdot 4\sqrt{3}=$$$$={48}^p\cdot 12$$$$$$$$S_n=\mathrm{\Sigma }(C_{n,k}\cdot 7^{n-k}\cdot {48}^p\cdot 12)$$$$({48}^p\cdot 12)\mathrm{mod}6=0\Rightarrow S_n\mathrm{mod}6=0$$

Commented by aba last updated on 17/Jan/23

$${\mathrm{S}}_{\mathrm{n}}=\frac{\sqrt{3}}{4}....$$

Commented by aba last updated on 17/Jan/23

$${\mathrm{a}}^{\mathrm{n}}-{\mathrm{b}}^{\mathrm{n}}=(\mathrm{a}-\mathrm{b})\left(\underset{\mathrm{k}=0}{\sum ^{\mathrm{n}-1}}{\mathrm{a}}^{\mathrm{k}}{\mathrm{b}}^{\mathrm{n}-1-\mathrm{k}}\right)$$$${\mathrm{S}}_{\mathrm{n}}=\frac{\sqrt{3}}{4}[8\sqrt{3}.\left(\underset{\mathrm{k}=0}{\sum ^{\mathrm{n}-1}}{(7+4\sqrt{3})}^{\mathrm{k}}{(7-4\sqrt{3})}^{\mathrm{n}-1-\mathrm{k}}\right)]$$$$=6\left(\underset{\mathrm{k}=0}{\sum ^{\mathrm{n}-1}}{(\sqrt{3}+2)}^{2\mathrm{k}}{(\sqrt{3}-2)}^{2(\mathrm{n}-1-\mathrm{k})}\right)$$$$\equiv 0\mathrm{mod}\left(6\right)$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com