Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 185424 by ajfour last updated on 21/Jan/23

Commented by Frix last updated on 21/Jan/23

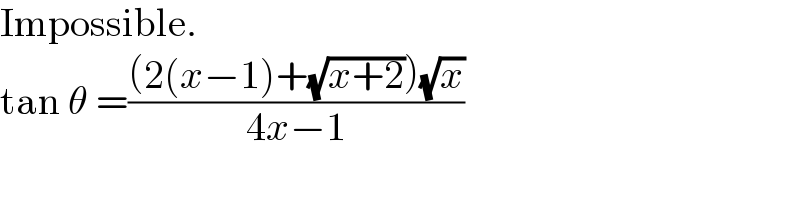
Impossible. tan θ =(((2(x−1)+(√(x+2)))(√x))/(4x−1))

$$\mathrm{Impossible}. \\ $$$$\mathrm{tan}\:\theta\:=\frac{\left(\mathrm{2}\left({x}−\mathrm{1}\right)+\sqrt{{x}+\mathrm{2}}\right)\sqrt{{x}}}{\mathrm{4}{x}−\mathrm{1}} \\ $$

Commented by MJS_new last updated on 22/Jan/23

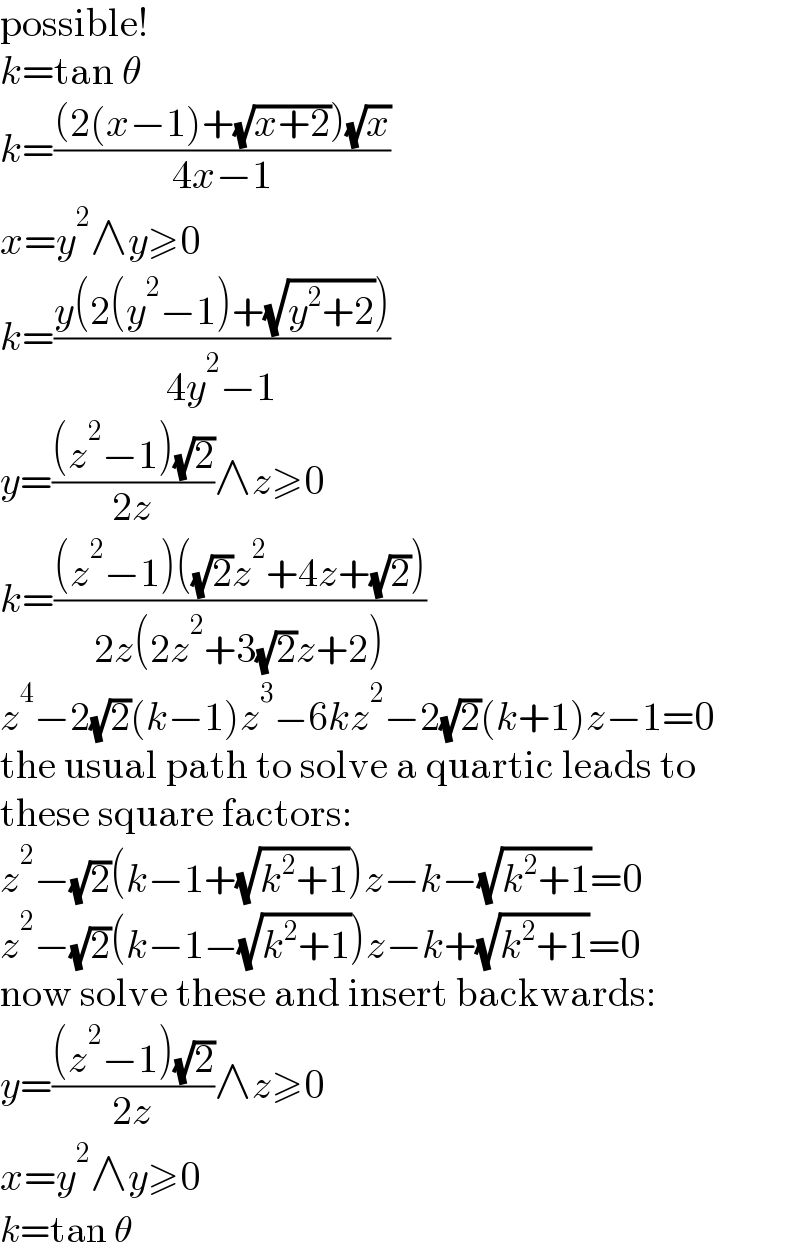
possible! k=tan θ k=(((2(x−1)+(√(x+2)))(√x))/(4x−1)) x=y^2 ∧y≥0 k=((y(2(y^2 −1)+(√(y^2 +2))))/(4y^2 −1)) y=(((z^2 −1)(√2))/(2z))∧z≥0 k=(((z^2 −1)((√2)z^2 +4z+(√2)))/(2z(2z^2 +3(√2)z+2))) z^4 −2(√2)(k−1)z^3 −6kz^2 −2(√2)(k+1)z−1=0 the usual path to solve a quartic leads to these square factors: z^2 −(√2)(k−1+(√(k^2 +1)))z−k−(√(k^2 +1))=0 z^2 −(√2)(k−1−(√(k^2 +1)))z−k+(√(k^2 +1))=0 now solve these and insert backwards: y=(((z^2 −1)(√2))/(2z))∧z≥0 x=y^2 ∧y≥0 k=tan θ

$$\mathrm{possible}! \\ $$$${k}=\mathrm{tan}\:\theta \\ $$$${k}=\frac{\left(\mathrm{2}\left({x}−\mathrm{1}\right)+\sqrt{{x}+\mathrm{2}}\right)\sqrt{{x}}}{\mathrm{4}{x}−\mathrm{1}} \\ $$$${x}={y}^{\mathrm{2}} \wedge{y}\geqslant\mathrm{0} \\ $$$${k}=\frac{{y}\left(\mathrm{2}\left({y}^{\mathrm{2}} −\mathrm{1}\right)+\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}\right)}{\mathrm{4}{y}^{\mathrm{2}} −\mathrm{1}} \\ $$$${y}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{2}}}{\mathrm{2}{z}}\wedge{z}\geqslant\mathrm{0} \\ $$$${k}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\left(\sqrt{\mathrm{2}}{z}^{\mathrm{2}} +\mathrm{4}{z}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}{z}\left(\mathrm{2}{z}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{2}}{z}+\mathrm{2}\right)} \\ $$$${z}^{\mathrm{4}} −\mathrm{2}\sqrt{\mathrm{2}}\left({k}−\mathrm{1}\right){z}^{\mathrm{3}} −\mathrm{6}{kz}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\left({k}+\mathrm{1}\right){z}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{usual}\:\mathrm{path}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{a}\:\mathrm{quartic}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{these}\:\mathrm{square}\:\mathrm{factors}: \\ $$$${z}^{\mathrm{2}} −\sqrt{\mathrm{2}}\left({k}−\mathrm{1}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right){z}−{k}−\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${z}^{\mathrm{2}} −\sqrt{\mathrm{2}}\left({k}−\mathrm{1}−\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right){z}−{k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{these}\:\mathrm{and}\:\mathrm{insert}\:\mathrm{backwards}: \\ $$$${y}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{2}}}{\mathrm{2}{z}}\wedge{z}\geqslant\mathrm{0} \\ $$$${x}={y}^{\mathrm{2}} \wedge{y}\geqslant\mathrm{0} \\ $$$${k}=\mathrm{tan}\:\theta \\ $$

Commented by Frix last updated on 21/Jan/23

Great!

$$\mathrm{Great}! \\ $$

Commented by ajfour last updated on 21/Jan/23

oh it created so much mess, i am so glad!

$${oh}\:{it}\:{created}\:{so}\:{much}\:{mess},\:{i}\:{am}\: \\ $$$${so}\:{glad}! \\ $$

Commented by MJS_new last updated on 21/Jan/23

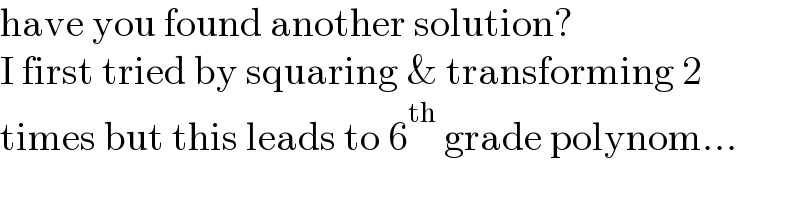
have you found another solution? I first tried by squaring & transforming 2 times but this leads to 6^(th) grade polynom...

$$\mathrm{have}\:\mathrm{you}\:\mathrm{found}\:\mathrm{another}\:\mathrm{solution}? \\ $$$$\mathrm{I}\:\mathrm{first}\:\mathrm{tried}\:\mathrm{by}\:\mathrm{squaring}\:\&\:\mathrm{transforming}\:\mathrm{2} \\ $$$$\mathrm{times}\:\mathrm{but}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{6}^{\mathrm{th}} \:\mathrm{grade}\:\mathrm{polynom}... \\ $$

Answered by mr W last updated on 21/Jan/23

(√((x+1)^2 −(x−1)^2 ))=tan (θ/2)+(x/(tan θ)) (x/(tan θ))−2(√x)+tan (θ/2)=0 ⇒(√x)=tan θ(1+(√(1−((tan (θ/2))/(tan θ))))) ⇒x=tan^2 θ (1+(√(1−((tan (θ/2))/(tan θ)))))^2

$$\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}+\frac{{x}}{\mathrm{tan}\:\theta} \\ $$$$\frac{{x}}{\mathrm{tan}\:\theta}−\mathrm{2}\sqrt{{x}}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{x}}=\mathrm{tan}\:\theta\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{tan}\:\theta}}\right) \\ $$$$\Rightarrow{x}=\mathrm{tan}^{\mathrm{2}} \:\theta\:\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{tan}\:\theta}}\right)^{\mathrm{2}} \\ $$

Commented by MJS_new last updated on 21/Jan/23

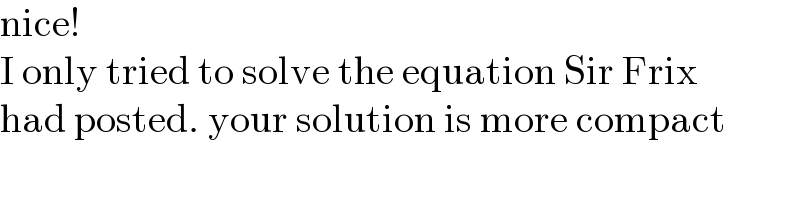
nice! I only tried to solve the equation Sir Frix had posted. your solution is more compact

$$\mathrm{nice}! \\ $$$$\mathrm{I}\:\mathrm{only}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{Sir}\:\mathrm{Frix} \\ $$$$\mathrm{had}\:\mathrm{posted}.\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{more}\:\mathrm{compact} \\ $$

Commented by MJS_new last updated on 21/Jan/23

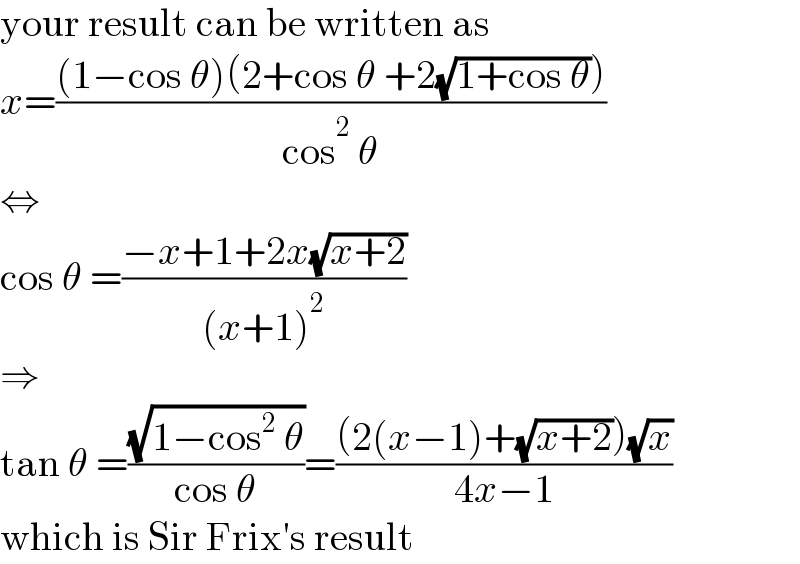
your result can be written as x=(((1−cos θ)(2+cos θ +2(√(1+cos θ))))/(cos^2 θ)) ⇔ cos θ =((−x+1+2x(√(x+2)))/((x+1)^2 )) ⇒ tan θ =((√(1−cos^2 θ))/(cos θ))=(((2(x−1)+(√(x+2)))(√x))/(4x−1)) which is Sir Frix′s result

$$\mathrm{your}\:\mathrm{result}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$${x}=\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\left(\mathrm{2}+\mathrm{cos}\:\theta\:+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\:\theta}\right)}{\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{cos}\:\theta\:=\frac{−{x}+\mathrm{1}+\mathrm{2}{x}\sqrt{{x}+\mathrm{2}}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{tan}\:\theta\:=\frac{\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta}}{\mathrm{cos}\:\theta}=\frac{\left(\mathrm{2}\left({x}−\mathrm{1}\right)+\sqrt{{x}+\mathrm{2}}\right)\sqrt{{x}}}{\mathrm{4}{x}−\mathrm{1}} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{Sir}\:\mathrm{Frix}'\mathrm{s}\:\mathrm{result} \\ $$

Commented by Ar Brandon last updated on 22/Jan/23

��������

Commented by Rasheed.Sindhi last updated on 22/Jan/23

������

Commented by Spillover last updated on 23/Jan/23

why are you loughing?

$${why}\:{are}\:{you}\:{loughing}?\: \\ $$

Commented by MJS_new last updated on 23/Jan/23

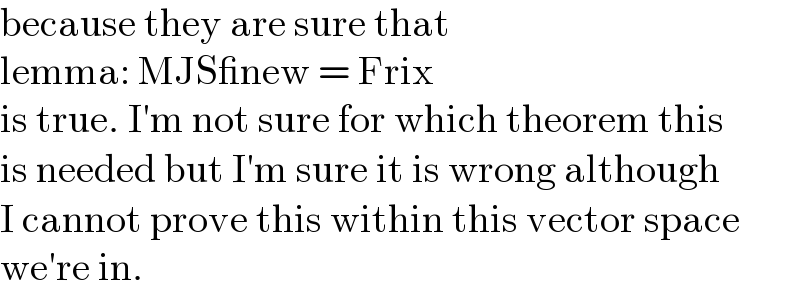
because they are sure that lemma: MJS_new = Frix is true. I′m not sure for which theorem this is needed but I′m sure it is wrong although I cannot prove this within this vector space we′re in.

$$\mathrm{because}\:\mathrm{they}\:\mathrm{are}\:\mathrm{sure}\:\mathrm{that} \\ $$$$\mathrm{lemma}:\:\mathrm{MJS\_new}\:=\:\mathrm{Frix} \\ $$$$\mathrm{is}\:\mathrm{true}.\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{for}\:\mathrm{which}\:\mathrm{theorem}\:\mathrm{this} \\ $$$$\mathrm{is}\:\mathrm{needed}\:\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{sure}\:\mathrm{it}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{although} \\ $$$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{prove}\:\mathrm{this}\:\mathrm{within}\:\mathrm{this}\:\mathrm{vector}\:\mathrm{space} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{in}. \\ $$

Commented by Frix last updated on 23/Jan/23

Anyway, it′s better to laugh than it is to cry...

$$\mathrm{Anyway},\:\mathrm{it}'\mathrm{s}\:\mathrm{better}\:\mathrm{to}\:\mathrm{laugh}\:\mathrm{than}\:\mathrm{it}\:\mathrm{is}\:\mathrm{to}\:\mathrm{cry}... \\ $$

Commented by Ar Brandon last updated on 23/Jan/23

Keep on entertaining us Sir MJFrix ��

Commented by Rasheed.Sindhi last updated on 23/Jan/23

MJS_new = Frix is itself a theorem, I think. (Please sir MJS/ Frix execuse us for our curiosity.)

$$\mathrm{MJS\_new}\:=\:\mathrm{Frix}\:{is}\:{itself}\:{a}\:{theorem},\: \\ $$$${I}\:{think}. \\ $$$$\left({Please}\:{sir}\:\mathrm{MJS}/\:\mathrm{Frix}\:{execuse}\:{us}\:\right. \\ $$$$\left.{for}\:{our}\:{curiosity}.\right) \\ $$

Commented by MJS_new last updated on 23/Jan/23

it′s ok. but why would I run 2 accounts? do I have too much time to spend?

$$\mathrm{it}'\mathrm{s}\:\mathrm{ok}. \\ $$$$\mathrm{but}\:\mathrm{why}\:\mathrm{would}\:\mathrm{I}\:\mathrm{run}\:\mathrm{2}\:\mathrm{accounts}?\:\mathrm{do}\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{too}\:\mathrm{much}\:\mathrm{time}\:\mathrm{to}\:\mathrm{spend}? \\ $$

Commented by Ar Brandon last updated on 23/Jan/23

Maybe her Majesty will be able to answer �� Good evening, sir MJFrix ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com