lim_(x→∞) x((√(4x^2 −12x+7))−(√(x^2 −4x−2))−x+1) lim_(x→∞) ((√(x^2 +3x))−((x^3 +2x^2 ))^(1/3) )


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 186066 by TUN last updated on 31/Jan/23

$\lim_{x \to \infty} x (\sqrt{4 x^{2} - 12 x + 7} - \sqrt{x^{2} - 4 x - 2} - x + 1)$ $\lim_{x \to \infty} (\sqrt{x^{2} + 3 x} - \sqrt[3]{x^{3} + 2 x^{2}})$
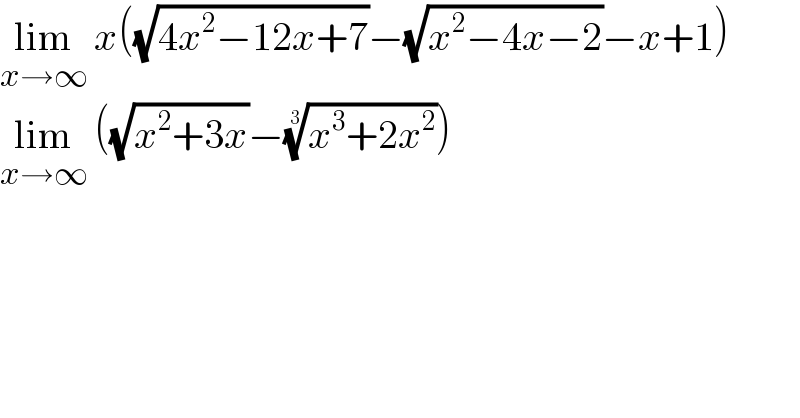
	Answered by a.lgnaoui last updated on 31/Jan/23

	$x (\sqrt{4 x^{2} - 12 x + 7} - \sqrt{x^{2} - 4 x - 2} - x + 1)$ $= 2 x \sqrt{x^{2} - 3 x + \frac{7}{4}} - x \sqrt{x^{2} - 4 x - 2} - x^{2} + x$ $\lim_{x \to \infty} [2 x \sqrt{x^{2} - 3 x + \frac{7}{4}} - x \sqrt{x^{2} - 4 x - 2} - (x^{2} - x)]$ $= \lim_{x \to \infty} [x (\frac{2 (4 x - 3 x + \frac{15}{4})}{\sqrt{x^{2} - 3 x + \frac{7}{4}} + \sqrt{x^{2} - 4 x - 2}}) - x (x - 1)]$ $[(\frac{2 x^{2}}{x \sqrt{1 - \frac{3}{x} + \frac{7}{4 x^{2}}} + x \sqrt{1 - \frac{4}{x} - \frac{2}{x^{2}}}}) - x^{2} (1 - \frac{1}{x})]$ $= \lim_{x \to \infty} x - x^{2} (1 - \frac{1}{x}) = \lim_{x \to \infty} (- x^{2}) = - \infty$
	Commented by Frix last updated on 01/Feb/23

	$Wrong .$
	Answered by Frix last updated on 01/Feb/23

	$\lim_{x \to \infty} x (\sqrt{4 x^{2} - 12 x + 7} - \sqrt{x^{2} - 4 x - 2} - x + 1) =$ $\lim_{t \to 0^{+}} \frac{t - 1 + \sqrt{7 t^{2} - 12 t + 4} - \sqrt{- 2 t^{2} + 4 t + 1}}{t^{2}} =$ $= \lim_{t \to 0^{+}} \frac{\frac{d^{2} [t - 1 + \sqrt{7 t^{2} - 12 t + 4} - \sqrt{- 2 t^{2} + 4 t + 1}]}{{d t}^{2}}}{\frac{d^{2} [t^{2}]}{{d t}^{2}}} =$ $= \lim_{t \to 0^{+}} \frac{\frac{6}{{(- 2 t^{2} - 4 t + 1)}^{\frac{3}{2}}} - \frac{8}{{(7 t^{2} - 12 t + 4)}^{\frac{3}{2}}}}{2} =$ $= \frac{5}{2}$ $Similar procedure for the 2^{nd} one leads to \frac{5}{6}$
	Answered by cortano1 last updated on 01/Feb/23

	$W i t h o u t L^{'} H o p i t a l$ $L = \lim_{x \to \infty} x [\sqrt{4 x^{2} - 12 x + 7} - \sqrt{x^{2} - 4 x - 2} - x + 1]$ $= \lim_{x \to \infty} x [\sqrt{4 x^{2} - 12 x + 7} - (2 x - 3) + (x - 2) - \sqrt{x^{2} - 4 x - 2}]$ $= \lim_{x \to \infty} x [\frac{- 2}{\sqrt{4 x^{2} - 12 x + 7} + (2 x - 3)} + \frac{6}{x - 2 + \sqrt{x^{2} - 4 x - 2}}]$ $= \frac{- 2}{\sqrt{4} + 2} + \frac{6}{1 + 1} = \frac{5}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum