Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 186074 by Mastermind last updated on 31/Jan/23

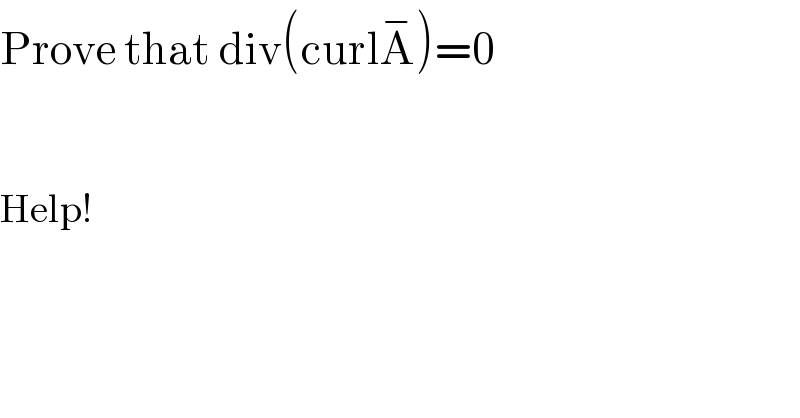
Prove that div(curlA^− )=0 Help!

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{div}\left(\mathrm{curl}\overset{−} {\mathrm{A}}\right)=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Answered by aleks041103 last updated on 30/Apr/23

Using einstein convention: div(curl(v))= =∂_i (ε_(ijk) ∂_j v_k )= =ε_(ijk) ∂_i ∂_j v_k = =−ε_(jik) ∂_i ∂_j v_k Schwartz rule : ∂_i ∂_j =∂_j ∂_i ⇒ε_(jik) ∂_i ∂_j v_k =ε_(jik) ∂_j ∂_i v_k renaming i→j and j→i ⇒ε_(jik) ∂_i ∂_j v_k =ε_(ijk) ∂_i ∂_j v_k =div(curl(v)) ⇒div(curl(v))=−div(curl(v)) ⇒div(curl(v))=0 Note: ε_(ijk) is the Levi−Civita symbol where ε_(ijk) = { ((+1, (ijk) is an even perm. of (123))),((−1, (ijk) is an odd perm. of (123))),((0, if any two of i,j or k are equal)) :} ⇒ε_(ijk) is completely antisymmetric, i.e. ε_(ijk) =−ε_(jik) Also, it is true that: a^→ =a_i e_i ^(→) , b^(→) =b_j e_j ^(→) a^→ ×b^(→) = ε_(ijk) a_i b_j e_k ^(→)

$${Using}\:{einstein}\:{convention}: \\ $$$${div}\left({curl}\left({v}\right)\right)= \\ $$$$=\partial_{{i}} \left(\varepsilon_{{ijk}} \partial_{{j}} {v}_{{k}} \right)= \\ $$$$=\varepsilon_{{ijk}} \partial_{{i}} \partial_{{j}} {v}_{{k}} = \\ $$$$=−\varepsilon_{{jik}} \partial_{{i}} \partial_{{j}} {v}_{{k}} \\ $$$${Schwartz}\:{rule}\::\:\partial_{{i}} \partial_{{j}} =\partial_{{j}} \partial_{{i}} \\ $$$$\Rightarrow\varepsilon_{{jik}} \partial_{{i}} \partial_{{j}} {v}_{{k}} =\varepsilon_{{jik}} \partial_{{j}} \partial_{{i}} {v}_{{k}} \\ $$$${renaming}\:{i}\rightarrow{j}\:{and}\:{j}\rightarrow{i} \\ $$$$\Rightarrow\varepsilon_{{jik}} \partial_{{i}} \partial_{{j}} {v}_{{k}} =\varepsilon_{{ijk}} \partial_{{i}} \partial_{{j}} {v}_{{k}} ={div}\left({curl}\left({v}\right)\right) \\ $$$$\Rightarrow{div}\left({curl}\left({v}\right)\right)=−{div}\left({curl}\left({v}\right)\right) \\ $$$$\Rightarrow{div}\left({curl}\left({v}\right)\right)=\mathrm{0} \\ $$$$ \\ $$$${Note}: \\ $$$$\varepsilon_{{ijk}} \:{is}\:{the}\:{Levi}−{Civita}\:{symbol} \\ $$$${where}\:\varepsilon_{{ijk}} =\begin{cases}{+\mathrm{1},\:\left({ijk}\right)\:{is}\:{an}\:{even}\:{perm}.\:{of}\:\left(\mathrm{123}\right)}\\{−\mathrm{1},\:\left({ijk}\right)\:{is}\:{an}\:{odd}\:{perm}.\:{of}\:\left(\mathrm{123}\right)}\\{\mathrm{0},\:{if}\:{any}\:{two}\:{of}\:{i},{j}\:{or}\:{k}\:{are}\:{equal}}\end{cases} \\ $$$$\Rightarrow\varepsilon_{{ijk}} \:{is}\:{completely}\:{antisymmetric},\:{i}.{e}. \\ $$$$\varepsilon_{{ijk}} =−\varepsilon_{{jik}} \\ $$$${Also},\:{it}\:{is}\:{true}\:{that}: \\ $$$$\overset{\rightarrow} {{a}}={a}_{{i}} \overset{\rightarrow} {{e}_{{i}} },\:\overset{\rightarrow} {{b}}={b}_{{j}} \overset{\rightarrow} {{e}_{{j}} } \\ $$$$\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\:=\:\varepsilon_{{ijk}} {a}_{{i}} {b}_{{j}} \:\overset{\rightarrow} {{e}_{{k}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com