
Question Number 1861 by 123456 last updated on 17/Oct/15
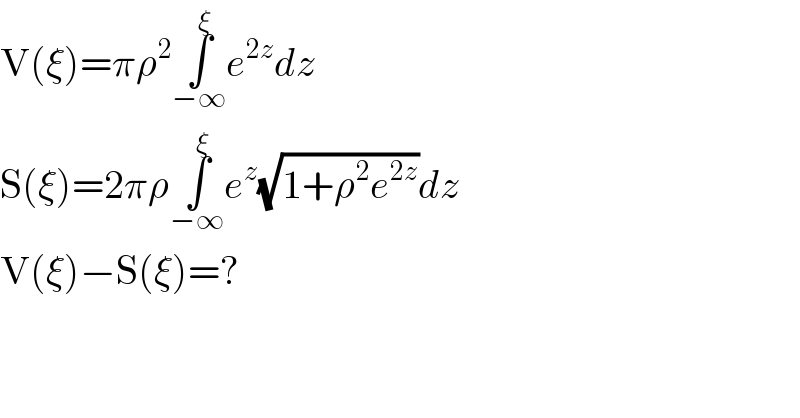
$$\mathrm{V}\left(\xi\right)=\pi\rho^{\mathrm{2}} \underset{−\infty} {\overset{\xi} {\int}}{e}^{\mathrm{2}{z}} {dz} \\ $$$$\mathrm{S}\left(\xi\right)=\mathrm{2}\pi\rho\underset{−\infty} {\overset{\xi} {\int}}{e}^{{z}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }{dz} \\ $$$$\mathrm{V}\left(\xi\right)−\mathrm{S}\left(\xi\right)=? \\ $$
Answered by 112358 last updated on 18/Oct/15
![V(ξ)=πρ^2 ∫_(−∞) ^ξ e^(2z) dz =πρ^2 lim_(p→−∞) ∫_p ^ξ e^(2z) dz =πρ^2 lim_(p→−∞) (e^(2z) /2)∣_p ^ξ =((πρ^2 )/2)lim_(p→−∞) (e^(2ξ) −e^(2p) ) =((πρ^2 )/2)(e^(2ξ) −lim_(p→−∞) e^(2p) ) =((πρ^2 e^(2ξ) )/2)−((πρ^2 )/2)×(1/∞) V(ξ)=((πρ^2 e^(2ξ) )/2) S(ξ)=2πρlim_(q→−∞) ∫_q ^ξ e^z (√(1+ρ^2 e^(2z) ))dz Let us set out to finding the indefinite integral I=∫e^z (√(1+ρ^2 e^(2z) ))dz . Let e^z =((tanθ)/ρ)⇒e^z dz=((sec^2 θ)/ρ)dθ. (√(1+ρ^2 e^(2x) ))=(√(1+ρ^2 ×((tan^2 θ)/ρ^2 ))) =(√(1+tan^2 θ))=(√(sec^2 θ))=secθ ∴ I=∫secθ×((sec^2 θ)/ρ)dθ I=(1/ρ)[secθtanθ−∫secθtan^2 θdθ] ρI=secθtanθ−∫sec^3 θ−secθdθ ρI=secθtanθ−∫sec^3 θdθ+∫secθdθ ρI=secθtanθ−ρI+ln∣secθ+tanθ∣ I=(1/(2ρ))[secθtanθ+ln∣secθ+tanθ∣] Since tanθ=ρe^z ⇒cosθ=(1/(√(1+ρ^2 e^(2z) ))) ⇒secθ=(√(1+ρ^2 e^(2z) )) ∴I=(1/(2ρ))[ρe^z (√(1+ρ^2 e^(2z) ))+ln(ρe^z +(√(1+ρ^2 e^(2z) )))]+c I=(1/2)e^z (√(1+ρ^2 e^(2z) ))+((sinh^(−1) (ρe^z ))/(2ρ))+c ∴ S(ξ)=πρlim_(q→−∞) [e^z (√(1+ρ^2 e^(2z) ))+((sinh^(−1) (ρe^z ))/ρ)]_q ^ξ S(ξ)=πρlim_(q→−∞) [e^ξ (√(1+ρ^2 e^(2ξ) ))+((sinh^(−1) (ρe^ξ ))/ρ)−e^q (√(1+ρ^2 e^(2q) ))−((sinh^(−1) (ρe^q ))/ρ)] S(ξ)=π(ρe^ξ (√(1+ρ^2 e^(2ξ) ))+sinh^(−1) (ρe^ξ )) ∴V(ξ)−S(ξ)=π[((ρ^2 e^(2ξ) )/2)−ρe^ξ (√(1+ρ^2 e^(2ξ) ))−sinh^(−1) (ρe^ξ )]](Q1866.png)
$${V}\left(\xi\right)=\pi\rho^{\mathrm{2}} \int_{−\infty} ^{\xi} {e}^{\mathrm{2}{z}} {dz} \\ $$$$\:\:\:\:\:\:\:\:\:=\pi\rho^{\mathrm{2}} \underset{{p}\rightarrow−\infty} {\mathrm{lim}}\int_{{p}} ^{\xi} {e}^{\mathrm{2}{z}} {dz} \\ $$$$\:\:\:\:\:\:\:\:\:=\pi\rho^{\mathrm{2}} \underset{{p}\rightarrow−\infty} {\mathrm{lim}}\frac{{e}^{\mathrm{2}{z}} }{\mathrm{2}}\mid_{{p}} ^{\xi} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\pi\rho^{\mathrm{2}} }{\mathrm{2}}\underset{{p}\rightarrow−\infty} {\mathrm{lim}}\left({e}^{\mathrm{2}\xi} −{e}^{\mathrm{2}{p}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\pi\rho^{\mathrm{2}} }{\mathrm{2}}\left({e}^{\mathrm{2}\xi} −\underset{{p}\rightarrow−\infty} {\mathrm{lim}}{e}^{\mathrm{2}{p}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\pi\rho^{\mathrm{2}} {e}^{\mathrm{2}\xi} }{\mathrm{2}}−\frac{\pi\rho^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{1}}{\infty} \\ $$$${V}\left(\xi\right)=\frac{\pi\rho^{\mathrm{2}} {e}^{\mathrm{2}\xi} }{\mathrm{2}} \\ $$$${S}\left(\xi\right)=\mathrm{2}\pi\rho\underset{{q}\rightarrow−\infty} {\mathrm{lim}}\int_{{q}} ^{\xi} {e}^{{z}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }{dz} \\ $$$${Let}\:{us}\:{set}\:{out}\:{to}\:{finding}\:{the}\: \\ $$$${indefinite}\:{integral}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:{I}=\int{e}^{{z}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }{dz}\:. \\ $$$${Let}\:{e}^{{z}} =\frac{{tan}\theta}{\rho}\Rightarrow{e}^{{z}} {dz}=\frac{{sec}^{\mathrm{2}} \theta}{\rho}{d}\theta. \\ $$$$\sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{x}} }=\sqrt{\mathrm{1}+\rho^{\mathrm{2}} ×\frac{{tan}^{\mathrm{2}} \theta}{\rho^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}=\sqrt{{sec}^{\mathrm{2}} \theta}={sec}\theta \\ $$$$\therefore\:{I}=\int{sec}\theta×\frac{{sec}^{\mathrm{2}} \theta}{\rho}{d}\theta \\ $$$${I}=\frac{\mathrm{1}}{\rho}\left[{sec}\theta{tan}\theta−\int{sec}\theta{tan}^{\mathrm{2}} \theta{d}\theta\right] \\ $$$$\rho{I}={sec}\theta{tan}\theta−\int{sec}^{\mathrm{3}} \theta−{sec}\theta{d}\theta \\ $$$$\rho{I}={sec}\theta{tan}\theta−\int{sec}^{\mathrm{3}} \theta{d}\theta+\int{sec}\theta{d}\theta \\ $$$$\rho{I}={sec}\theta{tan}\theta−\rho{I}+{ln}\mid{sec}\theta+{tan}\theta\mid \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\rho}\left[{sec}\theta{tan}\theta+{ln}\mid{sec}\theta+{tan}\theta\mid\right] \\ $$$${Since}\:{tan}\theta=\rho{e}^{{z}} \Rightarrow{cos}\theta=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }} \\ $$$$\Rightarrow{sec}\theta=\sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} } \\ $$$$\therefore{I}=\frac{\mathrm{1}}{\mathrm{2}\rho}\left[\rho{e}^{{z}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }+{ln}\left(\rho{e}^{{z}} +\sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }\right)\right]+{c} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{e}^{{z}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }+\frac{{sinh}^{−\mathrm{1}} \left(\rho{e}^{{z}} \right)}{\mathrm{2}\rho}+{c} \\ $$$$\therefore\:{S}\left(\xi\right)=\pi\rho\underset{{q}\rightarrow−\infty} {\mathrm{lim}}\left[{e}^{{z}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{z}} }+\frac{{sinh}^{−\mathrm{1}} \left(\rho{e}^{{z}} \right)}{\rho}\right]_{{q}} ^{\xi} \\ $$$${S}\left(\xi\right)=\pi\rho\underset{{q}\rightarrow−\infty} {\mathrm{lim}}\left[{e}^{\xi} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}\xi} }+\frac{{sinh}^{−\mathrm{1}} \left(\rho{e}^{\xi} \right)}{\rho}−{e}^{{q}} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}{q}} }−\frac{{sinh}^{−\mathrm{1}} \left(\rho{e}^{{q}} \right)}{\rho}\right] \\ $$$${S}\left(\xi\right)=\pi\left(\rho{e}^{\xi} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}\xi} }+{sinh}^{−\mathrm{1}} \left(\rho{e}^{\xi} \right)\right) \\ $$$$\therefore{V}\left(\xi\right)−{S}\left(\xi\right)=\pi\left[\frac{\rho^{\mathrm{2}} {e}^{\mathrm{2}\xi} }{\mathrm{2}}−\rho{e}^{\xi} \sqrt{\mathrm{1}+\rho^{\mathrm{2}} {e}^{\mathrm{2}\xi} }−{sinh}^{−\mathrm{1}} \left(\rho{e}^{\xi} \right)\right] \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
