Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 186551 by ajfour last updated on 05/Feb/23

Commented by mr W last updated on 06/Feb/23

square with side length 1? A_(shade) =((t^2 (t+2)^2 )/(4(1+t)[(1+t)^2 +1]))

$${square}\:{with}\:{side}\:{length}\:\mathrm{1}? \\ $$$${A}_{{shade}} =\frac{{t}^{\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{1}+{t}\right)\left[\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +\mathrm{1}\right]} \\ $$

Answered by ajfour last updated on 06/Feb/23

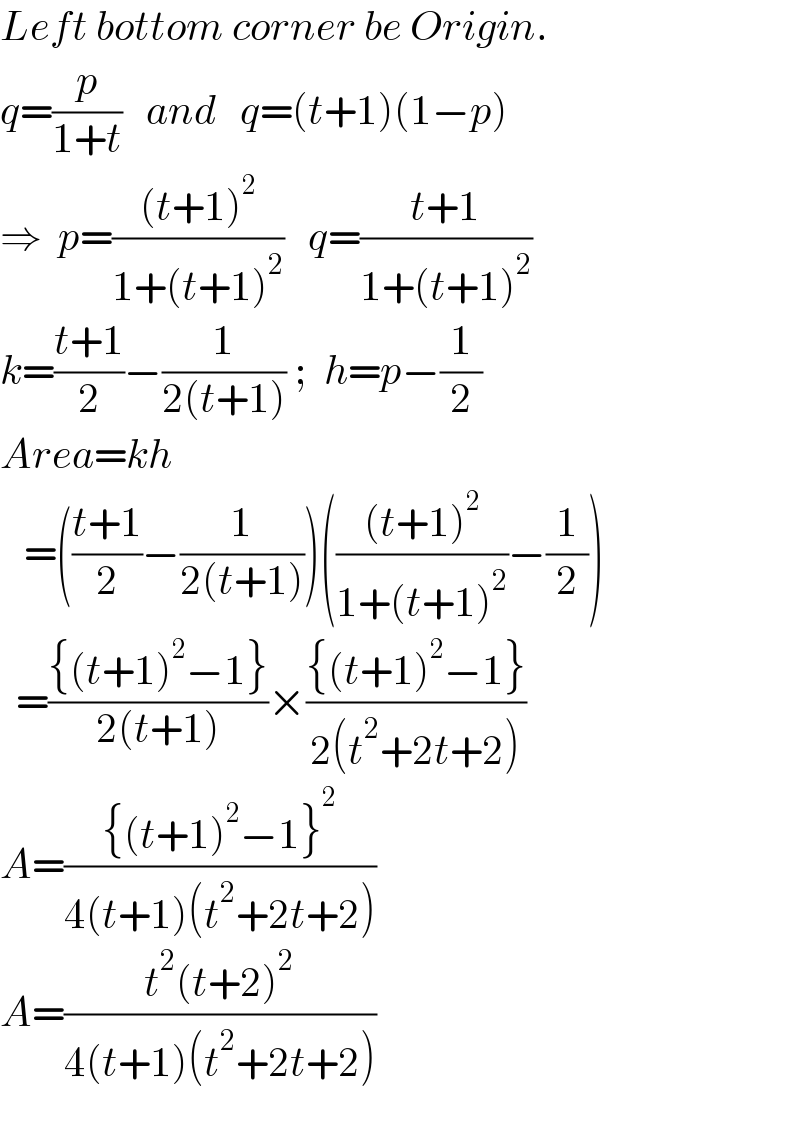
Left bottom corner be Origin. q=(p/(1+t)) and q=(t+1)(1−p) ⇒ p=(((t+1)^2 )/(1+(t+1)^2 )) q=((t+1)/(1+(t+1)^2 )) k=((t+1)/2)−(1/(2(t+1))) ; h=p−(1/2) Area=kh =(((t+1)/2)−(1/(2(t+1))))((((t+1)^2 )/(1+(t+1)^2 ))−(1/2)) =(({(t+1)^2 −1})/(2(t+1)))×(({(t+1)^2 −1})/(2(t^2 +2t+2))) A=(({(t+1)^2 −1}^2 )/(4(t+1)(t^2 +2t+2))) A=((t^2 (t+2)^2 )/(4(t+1)(t^2 +2t+2)))

$${Left}\:{bottom}\:{corner}\:{be}\:{Origin}. \\ $$$${q}=\frac{{p}}{\mathrm{1}+{t}}\:\:\:{and}\:\:\:{q}=\left({t}+\mathrm{1}\right)\left(\mathrm{1}−{p}\right) \\ $$$$\Rightarrow\:\:{p}=\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{1}+\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:{q}=\frac{{t}+\mathrm{1}}{\mathrm{1}+\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${k}=\frac{{t}+\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:;\:\:{h}={p}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${Area}={kh} \\ $$$$\:\:\:=\left(\frac{{t}+\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\right)\left(\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{1}+\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:=\frac{\left\{\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right\}}{\mathrm{2}\left({t}+\mathrm{1}\right)}×\frac{\left\{\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right\}}{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}\right)} \\ $$$${A}=\frac{\left\{\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right\}^{\mathrm{2}} }{\mathrm{4}\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}\right)} \\ $$$${A}=\frac{{t}^{\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}\right)} \\ $$$$\:\:\:\: \\ $$

Answered by mr W last updated on 06/Feb/23

Commented by mr W last updated on 06/Feb/23

h_2 =((1+t)/2) h_1 =(1/(2(1+t))) ((1−b)/h_3 )=((1+t)/1) ⇒(1/h_3 )=((1+t)/(1−b)) (b/h_3 )=(1/(1+t)) ⇒(1/h_3 )=(1/(b(1+t))) ((1+t)/(1−b))=(1/(b(1+t))) ⇒b=(1/((1+t)^2 +1)) A_(shade) =(h_2 −h_1 )((1/2)−b) =[((1+t)/2)−(1/(2(1+t)))][(1/2)−(1/((1+t)^2 +1))] =((t^2 (t+2)^2 )/(4(1+t)(t^2 +2t+2)))

$${h}_{\mathrm{2}} =\frac{\mathrm{1}+{t}}{\mathrm{2}} \\ $$$${h}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}\right)} \\ $$$$\frac{\mathrm{1}−{b}}{{h}_{\mathrm{3}} }=\frac{\mathrm{1}+{t}}{\mathrm{1}}\:\Rightarrow\frac{\mathrm{1}}{{h}_{\mathrm{3}} }=\frac{\mathrm{1}+{t}}{\mathrm{1}−{b}} \\ $$$$\frac{{b}}{{h}_{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{1}+{t}}\:\Rightarrow\frac{\mathrm{1}}{{h}_{\mathrm{3}} }=\frac{\mathrm{1}}{{b}\left(\mathrm{1}+{t}\right)} \\ $$$$\frac{\mathrm{1}+{t}}{\mathrm{1}−{b}}=\frac{\mathrm{1}}{{b}\left(\mathrm{1}+{t}\right)} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${A}_{{shade}} =\left({h}_{\mathrm{2}} −{h}_{\mathrm{1}} \right)\left(\frac{\mathrm{1}}{\mathrm{2}}−{b}\right) \\ $$$$\:\:\:\:\:=\left[\frac{\mathrm{1}+{t}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}\right)}\right]\left[\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$\:\:\:\:\:=\frac{{t}^{\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{1}+{t}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}\right)} \\ $$

Commented by ajfour last updated on 06/Feb/23

Thanks you Sir, I corrected!

$${Thanks}\:{you}\:{Sir},\:{I}\:{corrected}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com