
Question Number 1890 by Rasheed Soomro last updated on 21/Oct/15

$${Solve}\:{for}\:{x} \\ $$$$\:\:\:\:\:\:{tan}\:{x}\:+{tan}\:\mathrm{2}{x}\:−{tan}\:\mathrm{3}{x}\:=\mathrm{0} \\ $$$${Some}\:{one}\:{had}\:{posted}\:{this}\:{question}\:{and}\:{I}\:{had}\:{answered}\:{it} \\ $$$${but}\:{then}\:{thread}\:{was}\:{deleted}! \\ $$$${I}\:{think}\:{that}\:{the}\:{question}\:{is}\:{not}\:{importanceless}\:,\:{so}\:{I}\:{hav} \\ $$$${reposted}\:{it}. \\ $$
Commented by Rasheed Soomro last updated on 22/Oct/15

$${Question}\:{sholdn}'{t}\:{be}\:{deleted}/{changed}\:\:{in}\:{case}\:{it}\:{is}\:{answered}\:/{commented}. \\ $$$${Because}\:{after}\:{being}\:{answered}/{commented}\:{it}\:{is}\:{no}\:{longer} \\ $$$${remained}\:{your}\:{private}\:{matter}. \\ $$
Commented by 123456 last updated on 21/Oct/15
$$\mathrm{all}\:\mathrm{questions}\:\mathrm{are}\:\mathrm{importants}\::\mathrm{3} \\ $$
Commented by Rasheed Soomro last updated on 23/Oct/15

$${of}\:{course}! \\ $$
Answered by Yozzy last updated on 22/Oct/15

$${One}\:{method}\:{of}\:{approach}\:{involves}\:{the}\:{use}\:{of}\:{the}\:{following}\:{trigonometric}\:{identity}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tan}\mathrm{3}{x}=\frac{{tan}\mathrm{2}{x}+{tanx}}{\mathrm{1}−{tan}\mathrm{2}{xtanx}}..............\left(\mathrm{1}\right) \\ $$$${The}\:{given}\:{equation}\:{then}\:{takes}\:{the}\:{form},{after}\:{factorising}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({tanx}+{tan}\mathrm{2}{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{tanxtan}\mathrm{2}{x}}\right)=\mathrm{0}\:\:\left\{{tanxtan}\mathrm{2}{x}\neq\mathrm{1}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({tanx}+{tan}\mathrm{2}{x}\right)\left(\frac{\mathrm{1}−{tanxtan}\mathrm{2}{x}−\mathrm{1}}{\mathrm{1}−{tanxtan}\mathrm{2}{x}}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{tanxtan}\mathrm{2}{x}\left({tanx}+{tan}\mathrm{2}{x}\right)}{{tanxtan}\mathrm{2}{x}−\mathrm{1}}=\mathrm{0}.................\left(\mathrm{2}\right) \\ $$$${For}\:\left(\mathrm{2}\right)\:{to}\:{be}\:{true}\:{we}\:{have}\:{the}\:{possibility}\:{of}\:{tanx}=\mathrm{0}\:{or}\:{tan}\mathrm{2}{x}=\mathrm{0}\:{or}\:{tanx}+{tan}\mathrm{2}{x}=\mathrm{0}. \\ $$$${If}\:{tanx}=\mathrm{0}\:{we}\:{have}\:{a}\:{general}\:{solution}\:{as}\:{x}={n}\pi\:,\:{n}\in\mathbb{Z}. \\ $$$${If}\:{tan}\mathrm{2}{x}=\mathrm{0}\:{we}\:{have}\:{a}\:{general}\:{solution}\:{as}\:{x}=\frac{{n}\pi}{\mathrm{2}},\:{n}\in\mathbb{Z}. \\ $$$${If}\:{tanx}+{tan}\mathrm{2}{x}=\mathrm{0}\Rightarrow{tan}\mathrm{2}{x}=−{tanx}\Rightarrow\mathrm{2}{x}=−{x}+{n}\pi\Rightarrow{x}=\frac{{n}\pi}{\mathrm{3}},\:{n}\in\mathbb{Z}. \\ $$$${To}\:{check}\:{the}\:{last}\:{solution}\:{function}\:\left({since}\:{x}\:{is}\:{then}\:{a}\:{function}\:{of}\:{n}\right)\:{observe} \\ $$$${that}\:{from}\:\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tanx}+{tan}\mathrm{2}{x}={tan}\mathrm{3}{x}\left(\mathrm{1}−{tanxtan}\mathrm{2}{x}\right). \\ $$$${Having}\:{agreed}\:{upon}\:{that}\:{tanxtan}\mathrm{2}{x}\neq\mathrm{1}\Rightarrow{tanxtan}\mathrm{2}{x}−\mathrm{1}\neq\mathrm{0}.\:{Therefore}\:{we}\:{ought} \\ $$$${to}\:{have}\:{tan}\mathrm{3}{x}=\mathrm{0}\Rightarrow\mathrm{3}{x}={n}\pi\Rightarrow{x}=\frac{{n}\pi}{\mathrm{3}},\:{n}\in\mathbb{Z}. \\ $$$${Hence},\:{a}\:{possible}\:{general}\:{solution}\:{is}\:{given}\:{as} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\left\{{x}\in\mathbb{R},\:{n},{m},{q}\in\mathbb{Z}\mid{x}={n}\pi\:\vee\:{x}=\frac{{m}\pi}{\mathrm{2}}\:\vee\:{x}=\frac{{q}\pi}{\mathrm{3}}\right\}. \\ $$$${However},\:{if}\:{m}\:{is}\:{odd}\:{we}\:{that}\:{the}\:{equation}\:{is}\:{not}\:{satified}\:{since}\:{tan}\frac{{m}\pi}{\mathrm{2}}\:{is}\:{undefined} \\ $$$${for}\:{m}\:{odd}\:{so}\:{that}\:{we}\:{have}\:{the}\:{true}\:{solution}\:{set} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\left\{{x}\in\mathbb{R},{n},{q}\in\mathbb{Z}\mid{x}={n}\pi\vee{x}=\frac{{q}\pi}{\mathrm{3}}\right\}. \\ $$$${If}\:{tanxtan}\mathrm{2}{x}=\mathrm{1}\Rightarrow\mathrm{2}{tan}^{\mathrm{2}} {x}=\mathrm{1}−{tan}^{\mathrm{2}} {x}\Rightarrow{tan}^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{tanx}=\pm\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\Rightarrow{x}=\begin{cases}{\left(\frac{\mathrm{6}{n}+\mathrm{1}}{\mathrm{6}}\right)\pi\:\:\:{n}\in\mathbb{Z}}\\{\left(\frac{\mathrm{6}{n}−\mathrm{1}}{\mathrm{6}}\right)\pi\:\:{n}\in\mathbb{Z}\:\:}\end{cases} \\ $$$${The}\:{above}\:{general}\:{solution}\:{incurs}\:{a}\:{solution}\:{set}\:{S}^{'} \:{completely}\:{disjoint}\:{from} \\ $$$${S}\:{since}\:\mathrm{6}{n}\pm\mathrm{1}\:{is}\:{odd}\:\forall{n}\in\mathbb{Z}\Rightarrow\:\mathrm{6}\:{never}\:{divides}\:\mathrm{6}{n}\pm\mathrm{1}\:{to}\:{yield}\:{a}\:{quotient}\:{that}\:{is}\:{an} \\ $$$${integral}\:{multiple}\:{of}\:\mathrm{1},\:\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:\frac{\mathrm{1}}{\mathrm{3}}.\:{Therefore},\:{S}\:{appears}\:{to}\:{be}\:{the}\:{complete}\:{set}\:{of}\:{real}\: \\ $$$${solutions}.\:{I}\:{wonder}\:{what}\:{complex}\:{solutions}\:{exist}\:{for}\:{the}\:{equation}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 22/Oct/15
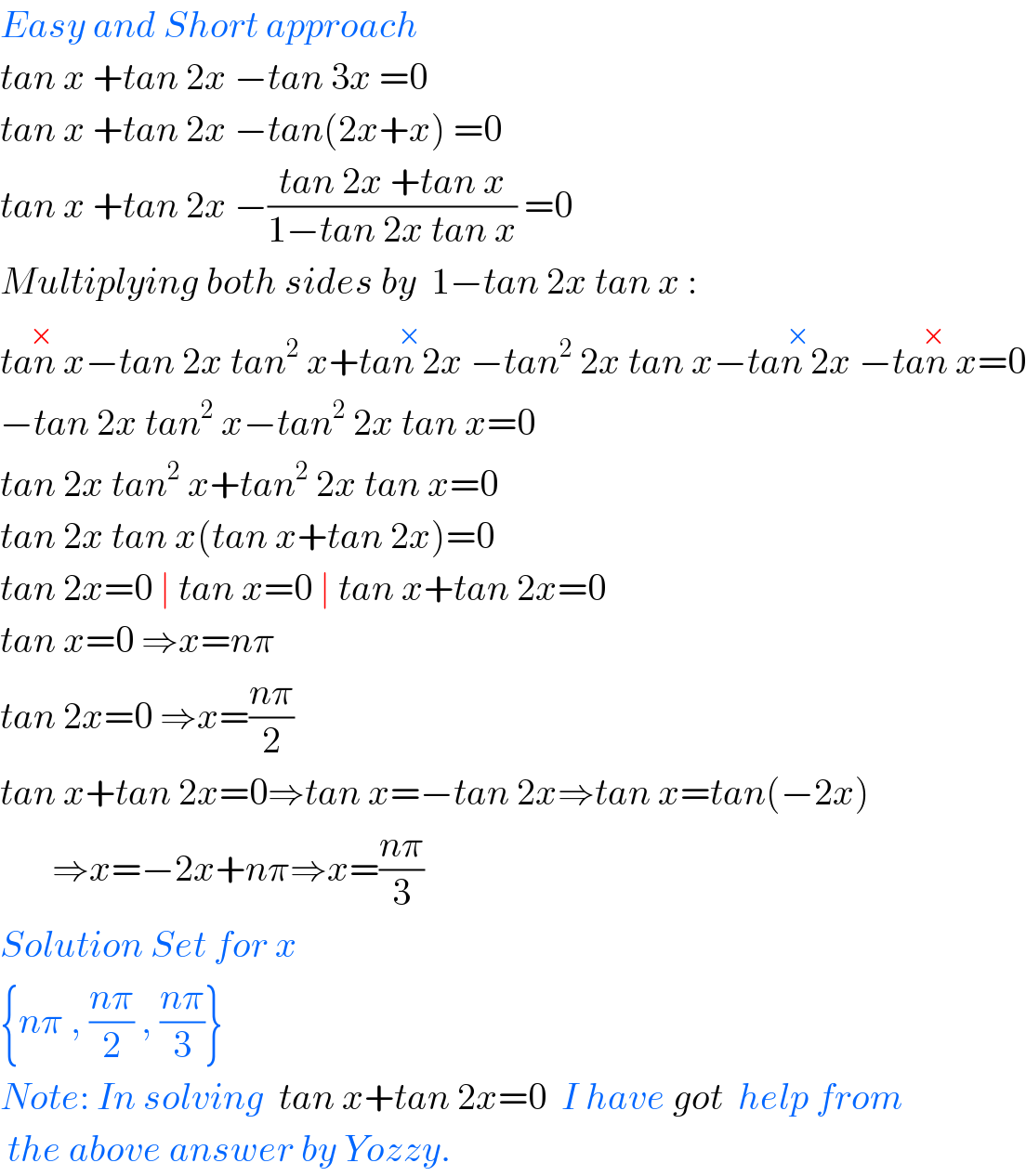
$${Easy}\:{and}\:{Short}\:{approach} \\ $$$${tan}\:{x}\:+{tan}\:\mathrm{2}{x}\:−{tan}\:\mathrm{3}{x}\:=\mathrm{0} \\ $$$${tan}\:{x}\:+{tan}\:\mathrm{2}{x}\:−{tan}\left(\mathrm{2}{x}+{x}\right)\:=\mathrm{0} \\ $$$${tan}\:{x}\:+{tan}\:\mathrm{2}{x}\:−\frac{{tan}\:\mathrm{2}{x}\:+{tan}\:{x}}{\mathrm{1}−{tan}\:\mathrm{2}{x}\:{tan}\:{x}}\:=\mathrm{0} \\ $$$${Multiplying}\:{both}\:{sides}\:{by}\:\:\mathrm{1}−{tan}\:\mathrm{2}{x}\:{tan}\:{x}\:: \\ $$$$\overset{×} {{tan}\:{x}}−{tan}\:\mathrm{2}{x}\:{tan}^{\mathrm{2}} \:{x}+\overset{×} {{tan}\:\mathrm{2}{x}}\:−{tan}^{\mathrm{2}} \:\mathrm{2}{x}\:{tan}\:{x}−\overset{×} {{tan}\:\mathrm{2}{x}}\:−\overset{×} {{tan}\:{x}}=\mathrm{0} \\ $$$$−{tan}\:\mathrm{2}{x}\:{tan}^{\mathrm{2}} \:{x}−{tan}^{\mathrm{2}} \:\mathrm{2}{x}\:{tan}\:{x}=\mathrm{0} \\ $$$${tan}\:\mathrm{2}{x}\:{tan}^{\mathrm{2}} \:{x}+{tan}^{\mathrm{2}} \:\mathrm{2}{x}\:{tan}\:{x}=\mathrm{0} \\ $$$${tan}\:\mathrm{2}{x}\:{tan}\:{x}\left({tan}\:{x}+{tan}\:\mathrm{2}{x}\right)=\mathrm{0} \\ $$$${tan}\:\mathrm{2}{x}=\mathrm{0}\:\mid\:{tan}\:{x}=\mathrm{0}\:\mid\:{tan}\:{x}+{tan}\:\mathrm{2}{x}=\mathrm{0} \\ $$$${tan}\:{x}=\mathrm{0}\:\Rightarrow{x}={n}\pi \\ $$$${tan}\:\mathrm{2}{x}=\mathrm{0}\:\Rightarrow{x}=\frac{{n}\pi}{\mathrm{2}} \\ $$$${tan}\:{x}+{tan}\:\mathrm{2}{x}=\mathrm{0}\Rightarrow{tan}\:{x}=−{tan}\:\mathrm{2}{x}\Rightarrow{tan}\:{x}={tan}\left(−\mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:\:\Rightarrow{x}=−\mathrm{2}{x}+{n}\pi\Rightarrow{x}=\frac{{n}\pi}{\mathrm{3}} \\ $$$${Solution}\:{Set}\:{for}\:{x} \\ $$$$\left\{{n}\pi\:,\:\frac{{n}\pi}{\mathrm{2}}\:,\:\frac{{n}\pi}{\mathrm{3}}\right\} \\ $$$${Note}:\:{In}\:{solving}\:\:{tan}\:{x}+{tan}\:\mathrm{2}{x}=\mathrm{0}\:\:{I}\:{have}\:{got}\:\:{help}\:{from} \\ $$$$\:{the}\:{above}\:{answer}\:{by}\:{Yozzy}. \\ $$
