
Question and Answers Forum
Question Number 1895 by Yozzy last updated on 22/Oct/15

Commented by Rasheed Soomro last updated on 23/Oct/15

Commented by Yozzy last updated on 23/Oct/15

Commented by Rasheed Soomro last updated on 23/Oct/15

Commented by Yozzy last updated on 23/Oct/15

Commented by Rasheed Soomro last updated on 23/Oct/15

Answered by Rasheed Soomro last updated on 25/Oct/15
![tan^(−1) (c+id)=a+ib Any of a and b depends on both c and d: a =(1/2)tan^(−1) (((2c)/(1−c^2 −d^2 ))) b=(1/(2i))tan^(−1) (((2id)/(1+c^2 +d^2 ))) −−−−−−−−−−−−−−−−− Proof: tan^(−1) (c+id)=a+ib ..............................(1) tan^(−1) (c−id)=a−ib [∵ tan z^(−) =tan z^(−) ]......(2) Adding (1) and (2) 2a=tan^(−1) (c+id)+tan^(−1) (c−id) =tan^(−1) (((c+id)+(c−id))/(1−(c+id)(c−id))) =tan^(−1) ((2c)/(1−(c^2 +d^2 ))) Or a =(1/2)tan^(−1) (((2c)/(1−c^2 −d^2 ))).................I(Proved) −−−−−−−−−−−−−−−− Similarly subtracting (2) from (1), we get 2ib=tan^(−1) (c+id)−tan^(−1) (c−id) =tan^(−1) (((c+id)−(c−id))/(1+(c+id)(c−id))) =tan^(−1) ((2id)/(1+c^2 +d^2 )) tan 2ib=((2id)/(1+c^2 +d^2 )) 2ib=tan^(−1) (((2id)/(1+c^2 +d^2 ))) b=(1/(2i))tan^(−1) (((2id)/(1+c^2 +d^2 )))...................II( Proved) −−−−−−−−−−−−−−−−−−−](Q1905.png)
Commented by Yozzy last updated on 23/Oct/15
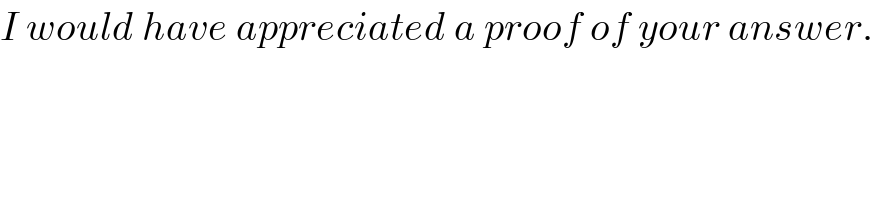
Commented by Yozzy last updated on 23/Oct/15

Answered by Yozzy last updated on 23/Oct/15
![tan^(−1) (c+id)=a+ib a,b,c,d∈R. ∴ c+id=tan(a+ib)=((tana+tanib)/(1−tanatanib)) Now, tanib=itanhb. ∴ c+id=((tana+itanhb)/(1−itanatanhb))⇒(c+id)(1−itanatanhb)=tana+itanhb c+dtanatanhb+i(d−ctanatanhb)=tana+itanhb Equating real and imaginary parts we get c+dtanatanhb=tana⇒tana(1−dtanhb)=c⇒tana=(c/(1−dtanhb)).......(i) And tanhb=d−ctanatanhb⇒tana=((d−tanhb)/(ctanhb))..........(ii) Since (i)=(ii)⇒ (c/(1−dtanhb))=((d−tanhb)/(ctanhb)). Let ω=tanhb. ∴ (c/(1−dω))=((d−ω)/(cω))⇒c^2 ω=(1−dω)(d−ω)=d−ω−d^2 ω+dω^2 dω^2 −(d^2 +1+c^2 )ω+d=0 This is a quadratic so ω=(((1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d)))/(2d)) ∴ tanhb=(((1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d)))/(2d)) (d≠0) and certainly (1+c^2 +d^2 )^2 >4d ∀c,d∈R Let y=tanh^(−1) x.⇒tanhy=x⇒sinhy=xcoshy e^y −e^(−y) =xe^y +xe^(−y) ×e^y : e^(2y) −1=xe^(2y) +x e^(2y) (1−x)=x+1⇒e^(2y) =((x+1)/(1−x))⇒2y=ln(((1+x)/(1−x)))⇒y=(1/2)ln(((1+x)/(1−x))) ∣x∣<1 (so y is real and defined) So b=tanh^(−1) [(((1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d)))/(2d))] with b∈R only if ∣(((1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d)))/(2d))∣<1 ⇒∣(1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d))∣<2∣d∣. If we assume this condition is satisfied we can find a. dtanhb=(((1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d)))/2) 1−dtanhb=((2−(1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d)))/2) ∴ tana=((2c)/(2−{(1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d))})) tana∈(−∞,+∞) so c and d can be such that the above equation is valid for any real c and d satisfying the condition ∣(1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d))∣<2∣d∣ ∴ a=tan^(−1) (((2c)/(2−{(1+c^2 +d^2 )±(√((1+c^2 +d^2 )^2 −4d))})))](Q1907.png)
Commented by Rasheed Soomro last updated on 23/Oct/15

Commented by Rasheed Soomro last updated on 23/Oct/15

Commented by Yozzy last updated on 23/Oct/15
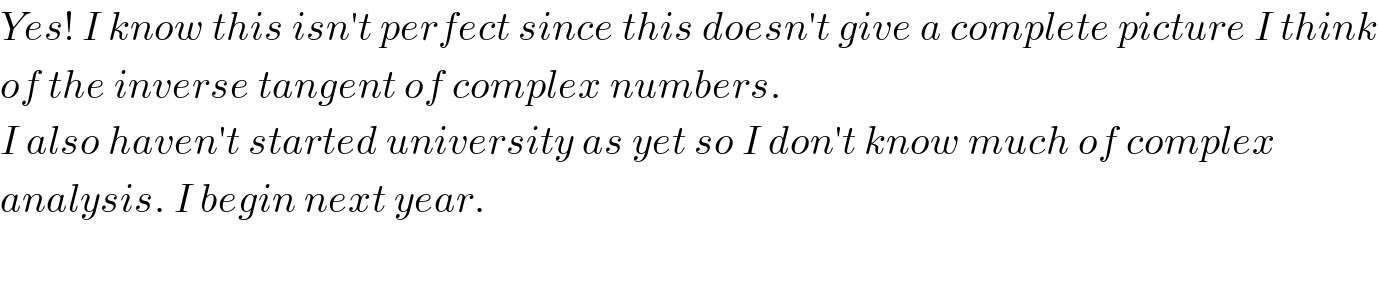
Commented by 123456 last updated on 23/Oct/15

Commented by Yozzy last updated on 24/Oct/15

