Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 18962 by Tinkutara last updated on 02/Aug/17

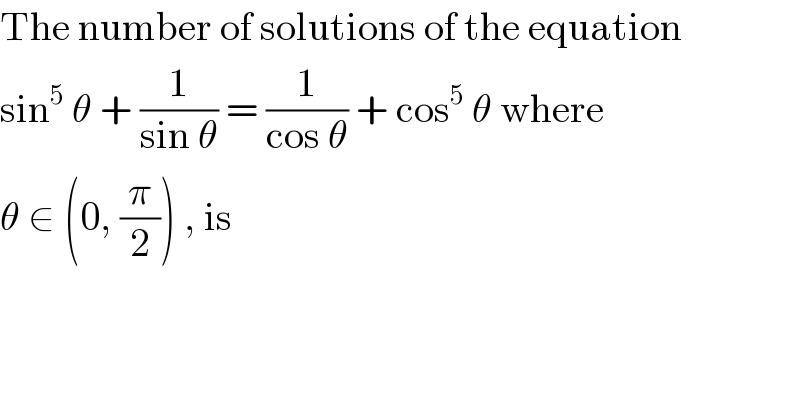
The number of solutions of the equation sin^5 θ + (1/(sin θ)) = (1/(cos θ)) + cos^5 θ where θ ∈ (0, (π/2)) , is

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{sin}^{\mathrm{5}} \:\theta\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:\theta}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\:+\:\mathrm{cos}^{\mathrm{5}} \:\theta\:\mathrm{where} \\ $$$$\theta\:\in\:\left(\mathrm{0},\:\frac{\pi}{\mathrm{2}}\right)\:,\:\mathrm{is} \\ $$

Answered by behi.8.3.4.1.7@gmail.com last updated on 02/Aug/17

sin^6 θ.cosθ+cosθ=sinθ+cos^6 θ.sinθ ⇒sinθ.cosθ(sin^5 θ−cos^5 θ)−(sinθ−cosθ)=0 sinθ=a,cosθ=b ⇒ab(a^5 −b^5 )−(a−b)=0 ⇒[ab(a^4 +a^3 b+a^2 b^2 +ab^3 +b^4 )−1](a−b)=0 1)a=b⇒sinθ=cosθ⇒tgθ=1⇒θ=kπ+(π/4),k∈Z 2)a^4 +b^4 =(a^2 +b^2 )^2 −2a^2 b^2 =1−2a^2 b^2 a^3 b+ab^3 =ab(a^2 +b^2 )=ab ⇒ab(1−2a^2 b^2 +a^2 b^2 +ab)−1=0 ⇒ab(1+ab−a^2 b^2 )−1=0 (ab=t) ⇒t(1+t−t^2 )−1=0⇒−t^3 +t^2 +t−1=0 ⇒t^3 −t^2 −t+1=0⇒t^2 (t−1)−(t−1)=0 ⇒(t−1)(t^2 −1)=0⇒(t−1)^2 (t+1)=0 ⇒t=1,−1⇒sinθ.cosθ=±1⇒sin2θ=±2 this eq. has not real answers.

$${sin}^{\mathrm{6}} \theta.{cos}\theta+{cos}\theta={sin}\theta+{cos}^{\mathrm{6}} \theta.{sin}\theta \\ $$$$\Rightarrow{sin}\theta.{cos}\theta\left({sin}^{\mathrm{5}} \theta−{cos}^{\mathrm{5}} \theta\right)−\left({sin}\theta−{cos}\theta\right)=\mathrm{0} \\ $$$${sin}\theta={a},{cos}\theta={b} \\ $$$$\Rightarrow{ab}\left({a}^{\mathrm{5}} −{b}^{\mathrm{5}} \right)−\left({a}−{b}\right)=\mathrm{0} \\ $$$$\Rightarrow\left[{ab}\left({a}^{\mathrm{4}} +{a}^{\mathrm{3}} {b}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{ab}^{\mathrm{3}} +{b}^{\mathrm{4}} \right)−\mathrm{1}\right]\left({a}−{b}\right)=\mathrm{0} \\ $$$$\left.\mathrm{1}\right){a}={b}\Rightarrow{sin}\theta={cos}\theta\Rightarrow{tg}\theta=\mathrm{1}\Rightarrow\theta={k}\pi+\frac{\pi}{\mathrm{4}},{k}\in{Z} \\ $$$$\left.\mathrm{2}\right){a}^{\mathrm{4}} +{b}^{\mathrm{4}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} {b}+{ab}^{\mathrm{3}} ={ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)={ab} \\ $$$$\Rightarrow{ab}\left(\mathrm{1}−\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{ab}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{ab}\left(\mathrm{1}+{ab}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)−\mathrm{1}=\mathrm{0}\:\:\:\left({ab}={t}\right) \\ $$$$\Rightarrow{t}\left(\mathrm{1}+{t}−{t}^{\mathrm{2}} \right)−\mathrm{1}=\mathrm{0}\Rightarrow−{t}^{\mathrm{3}} +{t}^{\mathrm{2}} +{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −{t}+\mathrm{1}=\mathrm{0}\Rightarrow{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)−\left({t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0}\Rightarrow\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{1},−\mathrm{1}\Rightarrow{sin}\theta.{cos}\theta=\pm\mathrm{1}\Rightarrow{sin}\mathrm{2}\theta=\pm\mathrm{2} \\ $$$${this}\:{eq}.\:{has}\:{not}\:{real}\:{answers}. \\ $$

Commented by Tinkutara last updated on 02/Aug/17

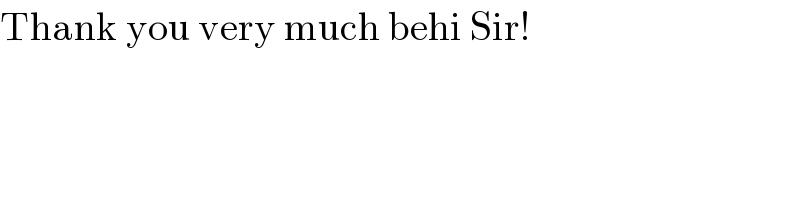
Thank you very much behi Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{behi}\:\mathrm{Sir}! \\ $$

Commented by behi.8.3.4.1.7@gmail.com last updated on 04/Aug/17

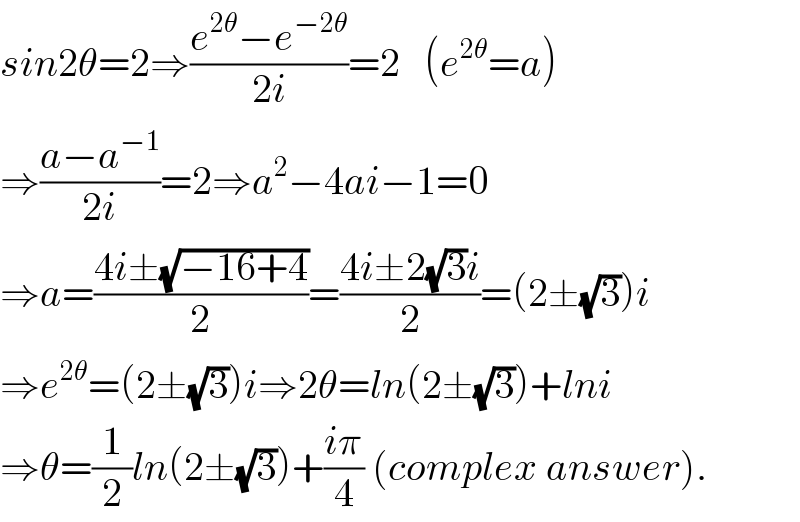
sin2θ=2⇒((e^(2θ) −e^(−2θ) )/(2i))=2 (e^(2θ) =a) ⇒((a−a^(−1) )/(2i))=2⇒a^2 −4ai−1=0 ⇒a=((4i±(√(−16+4)))/2)=((4i±2(√3)i)/2)=(2±(√3))i ⇒e^(2θ) =(2±(√3))i⇒2θ=ln(2±(√3))+lni ⇒θ=(1/2)ln(2±(√3))+((iπ)/4) (complex answer).

$${sin}\mathrm{2}\theta=\mathrm{2}\Rightarrow\frac{{e}^{\mathrm{2}\theta} −{e}^{−\mathrm{2}\theta} }{\mathrm{2}{i}}=\mathrm{2}\:\:\:\left({e}^{\mathrm{2}\theta} ={a}\right) \\ $$$$\Rightarrow\frac{{a}−{a}^{−\mathrm{1}} }{\mathrm{2}{i}}=\mathrm{2}\Rightarrow{a}^{\mathrm{2}} −\mathrm{4}{ai}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\mathrm{4}{i}\pm\sqrt{−\mathrm{16}+\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{4}{i}\pm\mathrm{2}\sqrt{\mathrm{3}}{i}}{\mathrm{2}}=\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right){i} \\ $$$$\Rightarrow{e}^{\mathrm{2}\theta} =\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right){i}\Rightarrow\mathrm{2}\theta={ln}\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)+{lni} \\ $$$$\Rightarrow\theta=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)+\frac{{i}\pi}{\mathrm{4}}\:\left({complex}\:{answer}\right). \\ $$

Commented by Tinkutara last updated on 04/Aug/17

But using this value in calculator does not gives 2. sin (ln (2 + (√3)) + ((iπ)/2)) = 2.423 + 0.578i

$$\mathrm{But}\:\mathrm{using}\:\mathrm{this}\:\mathrm{value}\:\mathrm{in}\:\mathrm{calculator}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{gives}\:\mathrm{2}.\:\mathrm{sin}\:\left(\mathrm{ln}\:\left(\mathrm{2}\:+\:\sqrt{\mathrm{3}}\right)\:+\:\frac{{i}\pi}{\mathrm{2}}\right) \\ $$$$=\:\mathrm{2}.\mathrm{423}\:+\:\mathrm{0}.\mathrm{578}{i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com