Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 1899 by Yozzy last updated on 22/Oct/15

Consider the system of equations 2yz+zx−5xy=2 yz−zx+2xy=1 yz−2zx+6xy=3. Show that xyz=±6 and find the possible values of x,y and z.

$${Consider}\:{the}\:{system}\:{of}\:{equations} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{yz}+{zx}−\mathrm{5}{xy}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{yz}−{zx}+\mathrm{2}{xy}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{yz}−\mathrm{2}{zx}+\mathrm{6}{xy}=\mathrm{3}. \\ $$$${Show}\:{that}\:{xyz}=\pm\mathrm{6}\: \\ $$$${and}\:{find}\:{the}\:{possible}\:{values} \\ $$$${of}\:{x},{y}\:{and}\:{z}. \\ $$

Commented by zainaltanjung last updated on 15/Oct/21

Consider the system of equations 2yz+zx−5xy=2 yz−zx+2xy=1 yz−2zx+6xy=3: Show that xyz=±6 and find the possible values of x;y and z

$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2yz}+\mathrm{zx}−\mathrm{5xy}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{yz}−\mathrm{zx}+\mathrm{2xy}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{yz}−\mathrm{2zx}+\mathrm{6xy}=\mathrm{3}: \\ $$$$\mathrm{Show}\:\mathrm{that}\:\mathrm{xyz}=\pm\mathrm{6}\: \\ $$$$\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{values} \\ $$$$\mathrm{of}\:\mathrm{x};\mathrm{y}\:\mathrm{and}\:\mathrm{z} \\ $$

Answered by 123456 last updated on 23/Oct/15

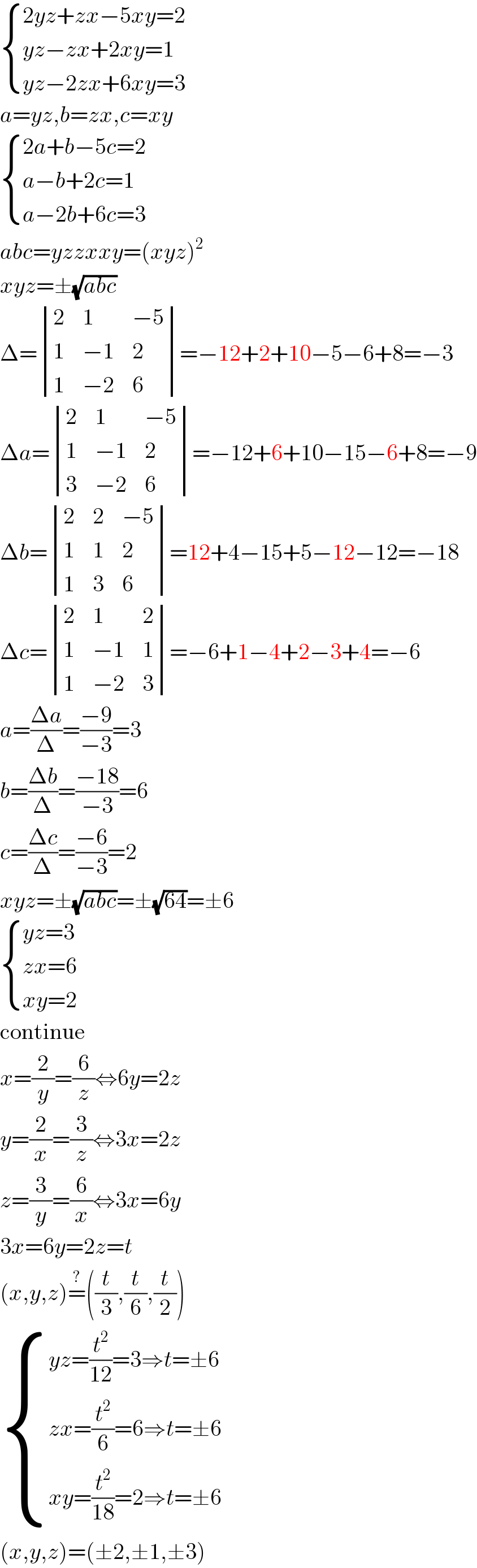
{ ((2yz+zx−5xy=2)),((yz−zx+2xy=1)),((yz−2zx+6xy=3)) :} a=yz,b=zx,c=xy { ((2a+b−5c=2)),((a−b+2c=1)),((a−2b+6c=3)) :} abc=yzzxxy=(xyz)^2 xyz=±(√(abc)) Δ= determinant ((2,1,(−5)),(1,(−1),2),(1,(−2),6))=−12+2+10−5−6+8=−3 Δa= determinant ((2,1,(−5)),(1,(−1),2),(3,(−2),6))=−12+6+10−15−6+8=−9 Δb= determinant ((2,2,(−5)),(1,1,2),(1,3,6))=12+4−15+5−12−12=−18 Δc= determinant ((2,1,2),(1,(−1),1),(1,(−2),3))=−6+1−4+2−3+4=−6 a=((Δa)/Δ)=((−9)/(−3))=3 b=((Δb)/Δ)=((−18)/(−3))=6 c=((Δc)/Δ)=((−6)/(−3))=2 xyz=±(√(abc))=±(√(64))=±6 { ((yz=3)),((zx=6)),((xy=2)) :} continue x=(2/y)=(6/z)⇔6y=2z y=(2/x)=(3/z)⇔3x=2z z=(3/y)=(6/x)⇔3x=6y 3x=6y=2z=t (x,y,z)=^? ((t/3),(t/6),(t/2)) { ((yz=(t^2 /(12))=3⇒t=±6)),((zx=(t^2 /6)=6⇒t=±6)),((xy=(t^2 /(18))=2⇒t=±6)) :} (x,y,z)=(±2,±1,±3)

$$\begin{cases}{\mathrm{2}{yz}+{zx}−\mathrm{5}{xy}=\mathrm{2}}\\{{yz}−{zx}+\mathrm{2}{xy}=\mathrm{1}}\\{{yz}−\mathrm{2}{zx}+\mathrm{6}{xy}=\mathrm{3}}\end{cases} \\ $$$${a}={yz},{b}={zx},{c}={xy} \\ $$$$\begin{cases}{\mathrm{2}{a}+{b}−\mathrm{5}{c}=\mathrm{2}}\\{{a}−{b}+\mathrm{2}{c}=\mathrm{1}}\\{{a}−\mathrm{2}{b}+\mathrm{6}{c}=\mathrm{3}}\end{cases} \\ $$$${abc}={yzzxxy}=\left({xyz}\right)^{\mathrm{2}} \\ $$$${xyz}=\pm\sqrt{{abc}} \\ $$$$\Delta=\begin{vmatrix}{\mathrm{2}}&{\mathrm{1}}&{−\mathrm{5}}\\{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{−\mathrm{2}}&{\mathrm{6}}\end{vmatrix}=−\mathrm{12}+\mathrm{2}+\mathrm{10}−\mathrm{5}−\mathrm{6}+\mathrm{8}=−\mathrm{3} \\ $$$$\Delta{a}=\begin{vmatrix}{\mathrm{2}}&{\mathrm{1}}&{−\mathrm{5}}\\{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{2}}\\{\mathrm{3}}&{−\mathrm{2}}&{\mathrm{6}}\end{vmatrix}=−\mathrm{12}+\mathrm{6}+\mathrm{10}−\mathrm{15}−\mathrm{6}+\mathrm{8}=−\mathrm{9} \\ $$$$\Delta{b}=\begin{vmatrix}{\mathrm{2}}&{\mathrm{2}}&{−\mathrm{5}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{6}}\end{vmatrix}=\mathrm{12}+\mathrm{4}−\mathrm{15}+\mathrm{5}−\mathrm{12}−\mathrm{12}=−\mathrm{18} \\ $$$$\Delta{c}=\begin{vmatrix}{\mathrm{2}}&{\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{−\mathrm{2}}&{\mathrm{3}}\end{vmatrix}=−\mathrm{6}+\mathrm{1}−\mathrm{4}+\mathrm{2}−\mathrm{3}+\mathrm{4}=−\mathrm{6} \\ $$$${a}=\frac{\Delta{a}}{\Delta}=\frac{−\mathrm{9}}{−\mathrm{3}}=\mathrm{3} \\ $$$${b}=\frac{\Delta{b}}{\Delta}=\frac{−\mathrm{18}}{−\mathrm{3}}=\mathrm{6} \\ $$$${c}=\frac{\Delta{c}}{\Delta}=\frac{−\mathrm{6}}{−\mathrm{3}}=\mathrm{2} \\ $$$${xyz}=\pm\sqrt{{abc}}=\pm\sqrt{\mathrm{64}}=\pm\mathrm{6} \\ $$$$\begin{cases}{{yz}=\mathrm{3}}\\{{zx}=\mathrm{6}}\\{{xy}=\mathrm{2}}\end{cases} \\ $$$$\mathrm{continue} \\ $$$${x}=\frac{\mathrm{2}}{{y}}=\frac{\mathrm{6}}{{z}}\Leftrightarrow\mathrm{6}{y}=\mathrm{2}{z} \\ $$$${y}=\frac{\mathrm{2}}{{x}}=\frac{\mathrm{3}}{{z}}\Leftrightarrow\mathrm{3}{x}=\mathrm{2}{z} \\ $$$${z}=\frac{\mathrm{3}}{{y}}=\frac{\mathrm{6}}{{x}}\Leftrightarrow\mathrm{3}{x}=\mathrm{6}{y} \\ $$$$\mathrm{3}{x}=\mathrm{6}{y}=\mathrm{2}{z}={t} \\ $$$$\left({x},{y},{z}\right)\overset{?} {=}\left(\frac{{t}}{\mathrm{3}},\frac{{t}}{\mathrm{6}},\frac{{t}}{\mathrm{2}}\right) \\ $$$$\begin{cases}{{yz}=\frac{{t}^{\mathrm{2}} }{\mathrm{12}}=\mathrm{3}\Rightarrow{t}=\pm\mathrm{6}}\\{{zx}=\frac{{t}^{\mathrm{2}} }{\mathrm{6}}=\mathrm{6}\Rightarrow{t}=\pm\mathrm{6}}\\{{xy}=\frac{{t}^{\mathrm{2}} }{\mathrm{18}}=\mathrm{2}\Rightarrow{t}=\pm\mathrm{6}}\end{cases} \\ $$$$\left({x},{y},{z}\right)=\left(\pm\mathrm{2},\pm\mathrm{1},\pm\mathrm{3}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com