∫_0 ^(π/2) (dx/(√(1+sin x))) ?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 95848 by john santu last updated on 28/May/20

$\underset{0}{\int^{\frac{π}{2}}} \frac{dx}{\sqrt{1 + \sin x}} ?$
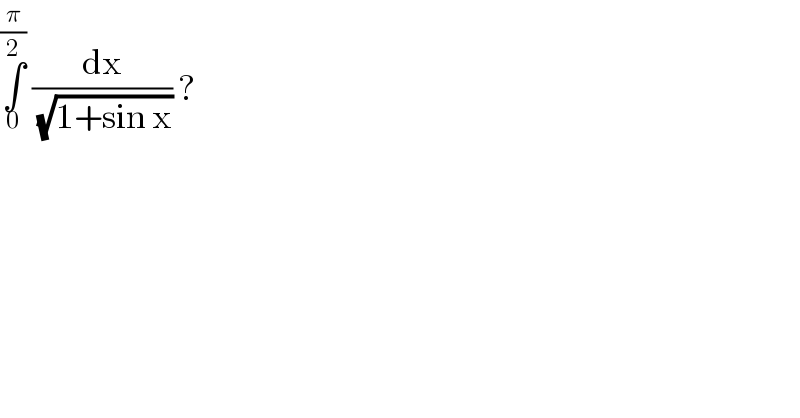
	Answered by bobhans last updated on 28/May/20

	$\underset{0}{\int^{\frac{π}{2}}} \frac{dx}{\sqrt{{(\sin \frac{x}{2} + \cos \frac{x}{2})}^{2}}} = \underset{0}{\int^{\frac{π}{2}}} \frac{dx}{\sqrt{2} \cos (\frac{x}{2} - \frac{π}{4})}$ $set \frac{x}{2} - \frac{π}{4} = t \Rightarrow dx = 2 dt$ $\underset{- \frac{π}{4}}{\int^{0}} \frac{2 dt}{\sqrt{2} \cos t} = \sqrt{2} [\ln ∣ \sec t + \tan t ∣]_{- \frac{π}{4}}^{0}$ $= \sqrt{2} \ln ∣ \frac{1 + \sin t}{\cos t} ∣ \underset{- \frac{π}{4}}{\overset{0}{}} = \sqrt{2} (0 - \ln (\sqrt{2} - 1)$ $= \sqrt{2} \ln (\frac{1}{\sqrt{2} - 1}) = \sqrt{2} \ln (\sqrt{2} + 1)$
	Answered by john santu last updated on 28/May/20
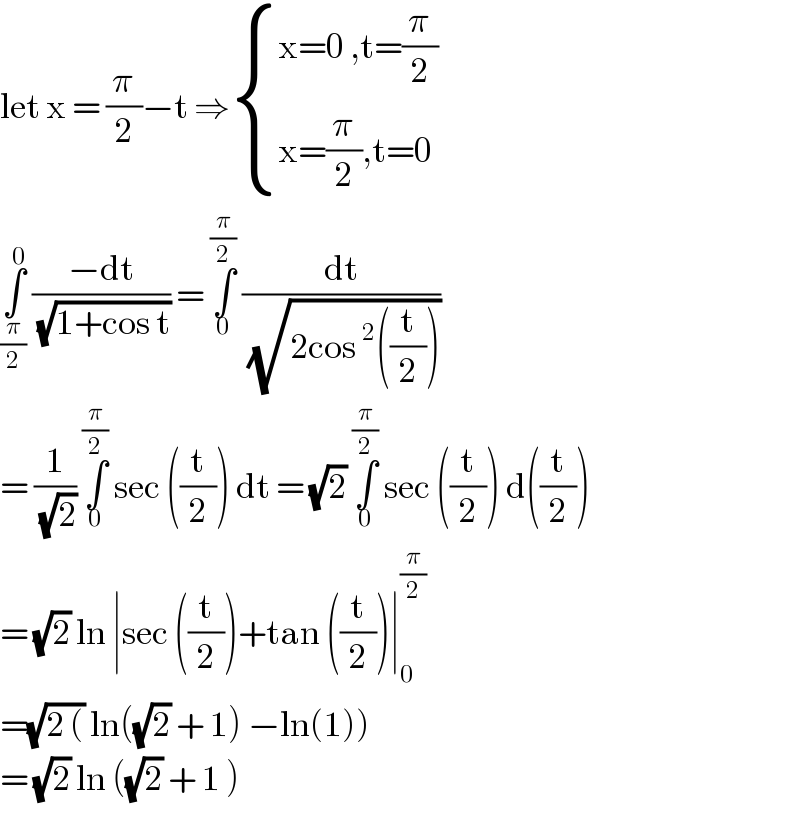
	$let x = (π/2)−t ⇒ { ((x=0 ,t=(π/2))),((x=(π/2),t=0)) :} ∫_(π/2) ^0 ((−dt)/(√(1+cos t))) = ∫_0 ^(π/2) (dt/(√(2cos^2 ((t/2))))) = (1/(√2)) ∫_0 ^(π/2) sec ((t/2)) dt = (√2) ∫_0 ^(π/2) sec ((t/2)) d((t/2)) = (√2) ln ∣sec ((t/2))+tan ((t/2))∣_0 ^(π/2) =(√(2 ()) ln((√2) + 1) −ln(1)) = (√2) ln ((√2) + 1 )$
	$let x = \frac{π}{2} - t \Rightarrow {\begin{cases} x = 0, t = \frac{π}{2} \\ x = \frac{π}{2}, t = 0 \end{cases}$ $\underset{\frac{π}{2}}{\int^{0}} \frac{- dt}{\sqrt{1 + \cos t}} = \underset{0}{\int^{\frac{π}{2}}} \frac{dt}{\sqrt{2 \cos^{2} (\frac{t}{2})}}$ $= \frac{1}{\sqrt{2}} \underset{0}{\int^{\frac{π}{2}}} \sec (\frac{t}{2}) dt = \sqrt{2} \underset{0}{\int^{\frac{π}{2}}} \sec (\frac{t}{2}) d (\frac{t}{2})$ $= \sqrt{2} \ln ∣ \sec (\frac{t}{2}) + \tan (\frac{t}{2}) ∣_{0}^{\frac{π}{2}}$ $= \sqrt{2 (} \ln (\sqrt{2} + 1) - \ln (1))$ $= \sqrt{2} \ln (\sqrt{2} + 1)$
	Answered by 1549442205 last updated on 28/May/20

	$putting \sqrt{1 + sinx} = t \Rightarrow t^{2} = 1 + sinx$ $\Rightarrow 2 tdt = cosxdx = \sqrt{1 - {(t^{2} - 1)}^{2}} dx$ $= t \sqrt{2 - t^{2}} dx . Hence, F (x) = \int \frac{2 dt}{t \sqrt{2 - t^{2}}}$ $putting \sqrt{2 - t^{2}} = u \Rightarrow \frac{- t}{\sqrt{2 - t^{2}}} dt = du \Rightarrow - tdt = udu$ $F = \int \frac{- 2 du}{2 - u^{2}} = \int \frac{2 du}{u^{2} - {(\sqrt{2})}^{2}} = \frac{1}{\sqrt{2}} \ln ∣ \frac{u - \sqrt{2}}{u + \sqrt{2}} ∣$ $\frac{1}{\sqrt{2}} \ln ∣ \frac{\sqrt{1 - sinx} - \sqrt{2}}{\sqrt{1 - \sin x} + \sqrt{2}} ∣ + C . Hence,$ $I = F (\frac{π}{2}) - F (0) = 0 - \frac{1}{\sqrt{2}} \ln \frac{\sqrt{2} - 1}{\sqrt{2} + 1}$ $= - \sqrt{2} \ln (\sqrt{2} - 1) = \sqrt{2} \ln (\sqrt{2} + 1)$
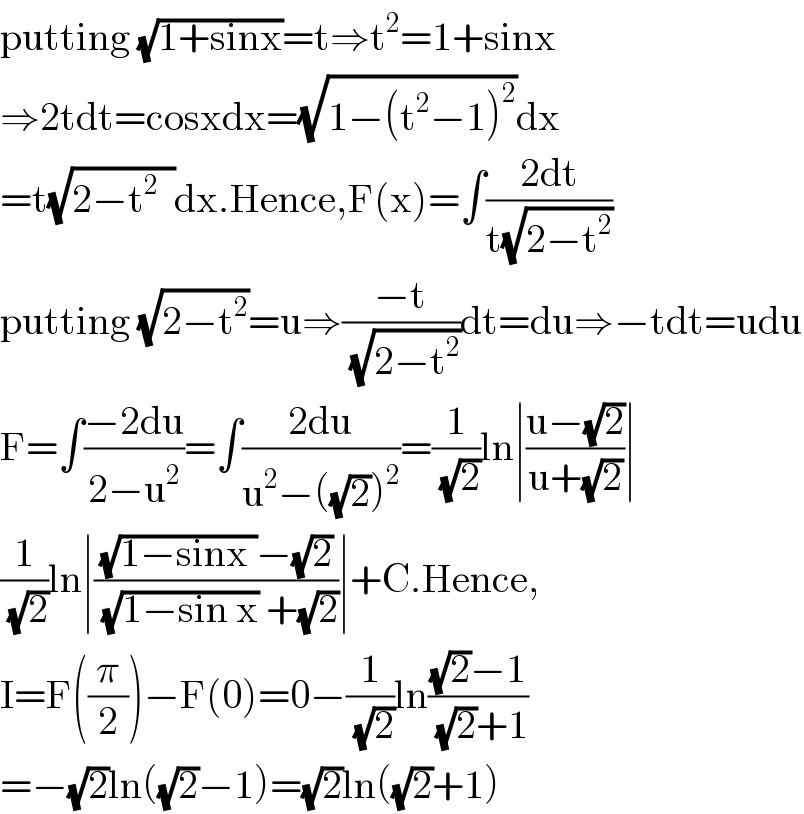
	Commented by john santu last updated on 28/May/20

	$oo you change it$
	Answered by mathmax by abdo last updated on 28/May/20
	$I =∫_0 ^(π/2) (dx/(√(1+sinx))) ⇒I =∫_0 ^(π/2) (dx/(√(cos^2 ((x/2))+sin^2 ((x/2)) +sin((x/2))cos((x/2))))) =∫_0 ^(π/2) (dx/(√((cos((x/2))+sin((x/2)))^2 ))) =∫_0 ^(π/2) (dx/(cos((x/2))+sin((x/2)))) =_((x/2)=t) ∫_0 ^(π/4) ((2dt)/(cost +sint)) =_(tan((t/2))=u) ∫_0 ^((√2)−1) ((4du)/((1+u^2 )(((1−u^2 )/(1+u^2 )) +((2u)/(1+u^2 ))))) =4 ∫_0 ^((√2)−1) (du/(1−u^2 +2u)) =−4 ∫_0 ^((√2)−1) (du/(u^2 −2u−1)) =−4 ∫_0 ^((√2)−1) (du/((u−1)^2 −2)) =−4 ∫_0 ^((√2)−1) (du/((u−1−(√2))(u−1+(√2)))) =((−4)/(2(√2)))∫_0 ^((√2)−1) {(1/(u−1−(√2)))−(1/(u−1+(√2)))}du =−(√2)[ln∣((u−1−(√2))/(u−1+(√2)))∣]_0 ^((√2)−1) =−(√2){ln∣((−2)/(2(√2)−2))∣−ln∣((1+(√2))/(−1+(√2)))∣} =−(√2){ln∣(1/(2−(√2)))∣−ln∣(((√2)+1)/((√2)−1))∣ =(√2){ln(2−(√2))+ln((((√2)+1)/((√2)−1)))}$
	$I = \int_{0}^{\frac{π}{2}} \frac{dx}{\sqrt{1 + sinx}} \Rightarrow I = \int_{0}^{\frac{π}{2}} \frac{dx}{\sqrt{\cos^{2} (\frac{x}{2}) + \sin^{2} (\frac{x}{2}) + \sin (\frac{x}{2}) \cos (\frac{x}{2})}}$ $= \int_{0}^{\frac{π}{2}} \frac{dx}{\sqrt{{(\cos (\frac{x}{2}) + \sin (\frac{x}{2}))}^{2}}} = \int_{0}^{\frac{π}{2}} \frac{dx}{\cos (\frac{x}{2}) + \sin (\frac{x}{2})} =_{\frac{x}{2} = t} \int_{0}^{\frac{π}{4}} \frac{2 dt}{cost + sint}$ $=_{\tan (\frac{t}{2}) = u} \int_{0}^{\sqrt{2} - 1} \frac{4 du}{(1 + u^{2}) (\frac{1 - u^{2}}{1 + u^{2}} + \frac{2 u}{1 + u^{2}})} = 4 \int_{0}^{\sqrt{2} - 1} \frac{du}{1 - u^{2} + 2 u}$ $= - 4 \int_{0}^{\sqrt{2} - 1} \frac{du}{u^{2} - 2 u - 1} = - 4 \int_{0}^{\sqrt{2} - 1} \frac{du}{{(u - 1)}^{2} - 2} = - 4 \int_{0}^{\sqrt{2} - 1} \frac{du}{(u - 1 - \sqrt{2}) (u - 1 + \sqrt{2})}$ $= \frac{- 4}{2 \sqrt{2}} \int_{0}^{\sqrt{2} - 1} {\frac{1}{u - 1 - \sqrt{2}} - \frac{1}{u - 1 + \sqrt{2}}} du$ $= - \sqrt{2} {[\ln ∣ \frac{u - 1 - \sqrt{2}}{u - 1 + \sqrt{2}} ∣]}_{0}^{\sqrt{2} - 1} = - \sqrt{2} {\ln ∣ \frac{- 2}{2 \sqrt{2} - 2} ∣ - \ln ∣ \frac{1 + \sqrt{2}}{- 1 + \sqrt{2}} ∣}$ $= - \sqrt{2} {\ln ∣ \frac{1}{2 - \sqrt{2}} ∣ - \ln ∣ \frac{\sqrt{2} + 1}{\sqrt{2} - 1} ∣ = \sqrt{2} {\ln (2 - \sqrt{2}) + \ln (\frac{\sqrt{2} + 1}{\sqrt{2} - 1})}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum