Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19198 by Tinkutara last updated on 07/Aug/17

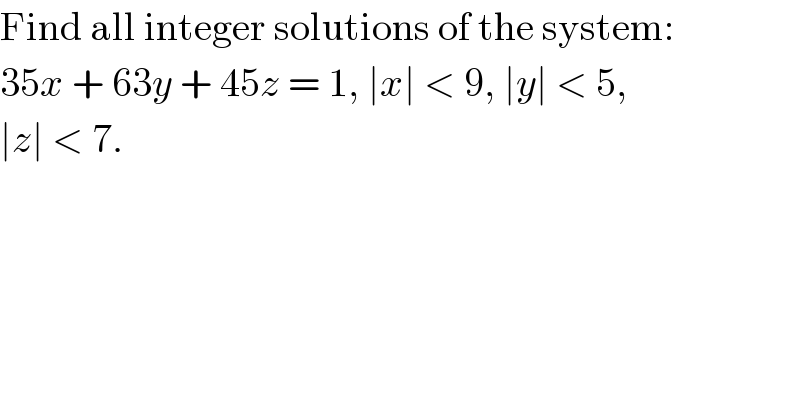
Find all integer solutions of the system: 35x + 63y + 45z = 1, ∣x∣ < 9, ∣y∣ < 5, ∣z∣ < 7.

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{integer}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{system}: \\ $$ $$\mathrm{35}{x}\:+\:\mathrm{63}{y}\:+\:\mathrm{45}{z}\:=\:\mathrm{1},\:\mid{x}\mid\:<\:\mathrm{9},\:\mid{y}\mid\:<\:\mathrm{5}, \\ $$ $$\mid{z}\mid\:<\:\mathrm{7}. \\ $$

Commented bymrW1 last updated on 09/Aug/17

(−10,2,5) (−1,−3,5) (8,−3,−2) (−1,2,−2) is this correct?

$$\left(−\mathrm{10},\mathrm{2},\mathrm{5}\right) \\ $$ $$\left(−\mathrm{1},−\mathrm{3},\mathrm{5}\right) \\ $$ $$\left(\mathrm{8},−\mathrm{3},−\mathrm{2}\right) \\ $$ $$\left(−\mathrm{1},\mathrm{2},−\mathrm{2}\right) \\ $$ $$\mathrm{is}\:\mathrm{this}\:\mathrm{correct}? \\ $$

Commented bymrW1 last updated on 13/Aug/17

what is kvs jmo?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{kvs}\:\mathrm{jmo}? \\ $$

Commented byTinkutara last updated on 13/Aug/17

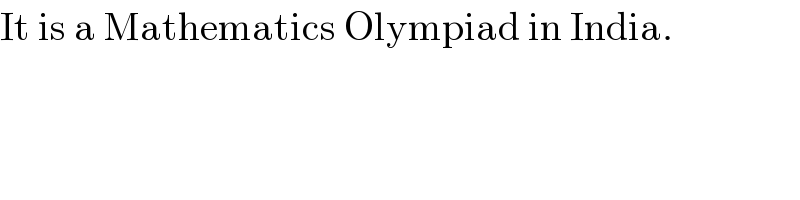
It is a Mathematics Olympiad in India.

$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{Mathematics}\:\mathrm{Olympiad}\:\mathrm{in}\:\mathrm{India}. \\ $$

Commented bymrW1 last updated on 13/Aug/17

Once you mentioned a nice book with many interesting mathematical questions. Can you tell me the book title and its author please.

$$\mathrm{Once}\:\mathrm{you}\:\mathrm{mentioned}\:\mathrm{a}\:\mathrm{nice}\:\mathrm{book}\:\mathrm{with} \\ $$ $$\mathrm{many}\:\mathrm{interesting}\:\mathrm{mathematical}\:\mathrm{questions}. \\ $$ $$\mathrm{Can}\:\mathrm{you}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{the}\:\mathrm{book}\:\mathrm{title}\:\mathrm{and}\:\mathrm{its} \\ $$ $$\mathrm{author}\:\mathrm{please}. \\ $$

Commented byTinkutara last updated on 13/Aug/17

bdmath.com/books Mathematical Olympiad Treasures Search for this book on the given site.

$$\mathrm{bdmath}.\mathrm{com}/\mathrm{books} \\ $$ $$\mathrm{Mathematical}\:\mathrm{Olympiad}\:\mathrm{Treasures} \\ $$ $$\mathrm{Search}\:\mathrm{for}\:\mathrm{this}\:\mathrm{book}\:\mathrm{on}\:\mathrm{the}\:\mathrm{given}\:\mathrm{site}. \\ $$

Commented bymrW1 last updated on 13/Aug/17

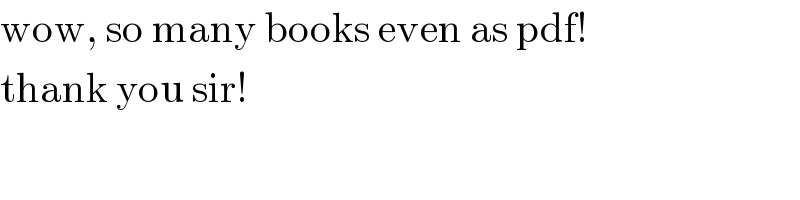
wow, so many books even as pdf! thank you sir!

$$\mathrm{wow},\:\mathrm{so}\:\mathrm{many}\:\mathrm{books}\:\mathrm{even}\:\mathrm{as}\:\mathrm{pdf}!\: \\ $$ $$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$

Commented byTawa1 last updated on 04/Oct/18

Sir, i don′t understand how to search the site. i typed bdmath.com/books. it is not showing anything sir

$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{to}\:\mathrm{search}\:\mathrm{the}\:\mathrm{site}. \\ $$ $$\mathrm{i}\:\mathrm{typed}\:\:\:\:\mathrm{bdmath}.\mathrm{com}/\mathrm{books}.\:\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{showing}\:\mathrm{anything}\:\mathrm{sir} \\ $$

Answered by mrW1 last updated on 13/Aug/17

let′s find at first the general solution of 35x + 63y + 45z = 1 ⇒7(5x+9y)+45z=1 ⇒5x+9y=u ...(i) ⇒7u+45z=1 ...(ii) a particular solution of (ii) is: u_1 =−32 and z_1 =5 the general solution of (ii) is: u=−32+45m z=5−7m (with m=any integer) a particular solution of 5x+9y=1 is x_1 =2 and y_1 =−1 the general solution of 5x+9y=1 is x=2+9k y=−1−5k (with k=any integer) the general solution of (i) is then x=(2+9k)u=2×(−32+45m)+9uk=−64+90m+9n y=(−1−5k)u=−1×(−32+45m)−5uk=32−45m−5n with n=uk=any integer the requested general solution for 35x + 63y + 45z = 1 is therefore: { ((x=−64+90m+9n)),((y=32−45m−5n)),((z=5−7m)) :} with m, n=any integer for ∣z∣<7 −7<5−7m<7 −12<−7m<2 12/7>m>−2/7 ⇒m=0, 1 with m=0 x=−64+9n y=32−5n for ∣x∣<9 −9<−64+9n<9 55<9n<73 55/9<n<73/9 ⇒n=7,8 (∗) for ∣y∣<5 −5<32−5n<5 −37<−5n<−27 37/5>n>27/5 ⇒n=6,7 (∗) ⇒m=0, n=7 with m=1 x=−64+90+9n=26+9n y=32−45−5n=−13−5n for ∣x∣<9 −9<26+9n<9 −35<9n<−17 −39/9<n<−17/9 ⇒n=−4,−3,−2 (∗) for ∣y∣<5 −5<−13−5n<5 8<−5n<18 −8/5>n>−18/5 ⇒n=−3,−2 (∗) ⇒m=1, n=−3 or −2 now we have totally 3 solutions (m,n)=(0,7), (1,−3),(1,−2) or (x,y,z)=(−1,−3,5) (x,y,z)=(−1,2,−2) (x,y,z)=(−8,−3,−2)

$$\mathrm{let}'\mathrm{s}\:\mathrm{find}\:\mathrm{at}\:\mathrm{first}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of} \\ $$ $$\mathrm{35}{x}\:+\:\mathrm{63}{y}\:+\:\mathrm{45}{z}\:=\:\mathrm{1} \\ $$ $$ \\ $$ $$\Rightarrow\mathrm{7}\left(\mathrm{5x}+\mathrm{9y}\right)+\mathrm{45z}=\mathrm{1} \\ $$ $$\Rightarrow\mathrm{5x}+\mathrm{9y}=\mathrm{u}\:\:\:...\left(\mathrm{i}\right) \\ $$ $$\Rightarrow\mathrm{7u}+\mathrm{45z}=\mathrm{1}\:\:...\left(\mathrm{ii}\right) \\ $$ $$ \\ $$ $$\mathrm{a}\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{of}\:\left(\mathrm{ii}\right)\:\mathrm{is}: \\ $$ $$\mathrm{u}_{\mathrm{1}} =−\mathrm{32}\:\mathrm{and}\:\mathrm{z}_{\mathrm{1}} =\mathrm{5} \\ $$ $$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\left(\mathrm{ii}\right)\:\mathrm{is}: \\ $$ $$\mathrm{u}=−\mathrm{32}+\mathrm{45m} \\ $$ $$\mathrm{z}=\mathrm{5}−\mathrm{7m}\:\left(\mathrm{with}\:\mathrm{m}=\mathrm{any}\:\mathrm{integer}\right) \\ $$ $$ \\ $$ $$\mathrm{a}\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{5x}+\mathrm{9y}=\mathrm{1}\:\mathrm{is} \\ $$ $$\mathrm{x}_{\mathrm{1}} =\mathrm{2}\:\mathrm{and}\:\mathrm{y}_{\mathrm{1}} =−\mathrm{1} \\ $$ $$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{5x}+\mathrm{9y}=\mathrm{1}\:\mathrm{is} \\ $$ $$\mathrm{x}=\mathrm{2}+\mathrm{9k} \\ $$ $$\mathrm{y}=−\mathrm{1}−\mathrm{5k}\:\left(\mathrm{with}\:\mathrm{k}=\mathrm{any}\:\mathrm{integer}\right) \\ $$ $$ \\ $$ $$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\left(\mathrm{i}\right)\:\mathrm{is}\:\mathrm{then} \\ $$ $$\mathrm{x}=\left(\mathrm{2}+\mathrm{9k}\right)\mathrm{u}=\mathrm{2}×\left(−\mathrm{32}+\mathrm{45m}\right)+\mathrm{9uk}=−\mathrm{64}+\mathrm{90m}+\mathrm{9n} \\ $$ $$\mathrm{y}=\left(−\mathrm{1}−\mathrm{5k}\right)\mathrm{u}=−\mathrm{1}×\left(−\mathrm{32}+\mathrm{45m}\right)−\mathrm{5uk}=\mathrm{32}−\mathrm{45m}−\mathrm{5n} \\ $$ $$\mathrm{with}\:\mathrm{n}=\mathrm{uk}=\mathrm{any}\:\mathrm{integer} \\ $$ $$ \\ $$ $$\mathrm{the}\:\mathrm{requested}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{for} \\ $$ $$\mathrm{35}\boldsymbol{{x}}\:+\:\mathrm{63}\boldsymbol{{y}}\:+\:\mathrm{45}\boldsymbol{{z}}\:=\:\mathrm{1} \\ $$ $$\mathrm{is}\:\mathrm{therefore}: \\ $$ $$\begin{cases}{\mathrm{x}=−\mathrm{64}+\mathrm{90m}+\mathrm{9n}}\\{\mathrm{y}=\mathrm{32}−\mathrm{45m}−\mathrm{5n}}\\{\mathrm{z}=\mathrm{5}−\mathrm{7m}}\end{cases} \\ $$ $$\mathrm{with}\:\mathrm{m},\:\mathrm{n}=\mathrm{any}\:\mathrm{integer} \\ $$ $$ \\ $$ $$\mathrm{for}\:\mid\mathrm{z}\mid<\mathrm{7} \\ $$ $$−\mathrm{7}<\mathrm{5}−\mathrm{7m}<\mathrm{7} \\ $$ $$−\mathrm{12}<−\mathrm{7m}<\mathrm{2} \\ $$ $$\mathrm{12}/\mathrm{7}>\mathrm{m}>−\mathrm{2}/\mathrm{7} \\ $$ $$\Rightarrow\mathrm{m}=\mathrm{0},\:\mathrm{1} \\ $$ $$ \\ $$ $$\mathrm{with}\:\mathrm{m}=\mathrm{0} \\ $$ $$\mathrm{x}=−\mathrm{64}+\mathrm{9n} \\ $$ $$\mathrm{y}=\mathrm{32}−\mathrm{5n} \\ $$ $$\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{9} \\ $$ $$−\mathrm{9}<−\mathrm{64}+\mathrm{9n}<\mathrm{9} \\ $$ $$\mathrm{55}<\mathrm{9n}<\mathrm{73} \\ $$ $$\mathrm{55}/\mathrm{9}<\mathrm{n}<\mathrm{73}/\mathrm{9} \\ $$ $$\Rightarrow\mathrm{n}=\mathrm{7},\mathrm{8}\:\:\:\left(\ast\right) \\ $$ $$\mathrm{for}\:\mid\mathrm{y}\mid<\mathrm{5} \\ $$ $$−\mathrm{5}<\mathrm{32}−\mathrm{5n}<\mathrm{5} \\ $$ $$−\mathrm{37}<−\mathrm{5n}<−\mathrm{27} \\ $$ $$\mathrm{37}/\mathrm{5}>\mathrm{n}>\mathrm{27}/\mathrm{5} \\ $$ $$\Rightarrow\mathrm{n}=\mathrm{6},\mathrm{7}\:\:\:\left(\ast\right) \\ $$ $$\Rightarrow\mathrm{m}=\mathrm{0},\:\mathrm{n}=\mathrm{7} \\ $$ $$ \\ $$ $$\mathrm{with}\:\mathrm{m}=\mathrm{1} \\ $$ $$\mathrm{x}=−\mathrm{64}+\mathrm{90}+\mathrm{9n}=\mathrm{26}+\mathrm{9n} \\ $$ $$\mathrm{y}=\mathrm{32}−\mathrm{45}−\mathrm{5n}=−\mathrm{13}−\mathrm{5n} \\ $$ $$\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{9} \\ $$ $$−\mathrm{9}<\mathrm{26}+\mathrm{9n}<\mathrm{9} \\ $$ $$−\mathrm{35}<\mathrm{9n}<−\mathrm{17} \\ $$ $$−\mathrm{39}/\mathrm{9}<\mathrm{n}<−\mathrm{17}/\mathrm{9} \\ $$ $$\Rightarrow\mathrm{n}=−\mathrm{4},−\mathrm{3},−\mathrm{2}\:\:\:\left(\ast\right) \\ $$ $$\mathrm{for}\:\mid\mathrm{y}\mid<\mathrm{5} \\ $$ $$−\mathrm{5}<−\mathrm{13}−\mathrm{5n}<\mathrm{5} \\ $$ $$\mathrm{8}<−\mathrm{5n}<\mathrm{18} \\ $$ $$−\mathrm{8}/\mathrm{5}>\mathrm{n}>−\mathrm{18}/\mathrm{5} \\ $$ $$\Rightarrow\mathrm{n}=−\mathrm{3},−\mathrm{2}\:\:\:\left(\ast\right) \\ $$ $$\Rightarrow\mathrm{m}=\mathrm{1},\:\mathrm{n}=−\mathrm{3}\:\mathrm{or}\:−\mathrm{2} \\ $$ $$ \\ $$ $$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{totally}\:\mathrm{3}\:\mathrm{solutions} \\ $$ $$\left(\mathrm{m},\mathrm{n}\right)=\left(\mathrm{0},\mathrm{7}\right),\:\left(\mathrm{1},−\mathrm{3}\right),\left(\mathrm{1},−\mathrm{2}\right) \\ $$ $$\mathrm{or} \\ $$ $$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(−\mathrm{1},−\mathrm{3},\mathrm{5}\right) \\ $$ $$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(−\mathrm{1},\mathrm{2},−\mathrm{2}\right) \\ $$ $$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(−\mathrm{8},−\mathrm{3},−\mathrm{2}\right) \\ $$

Commented byTinkutara last updated on 13/Aug/17

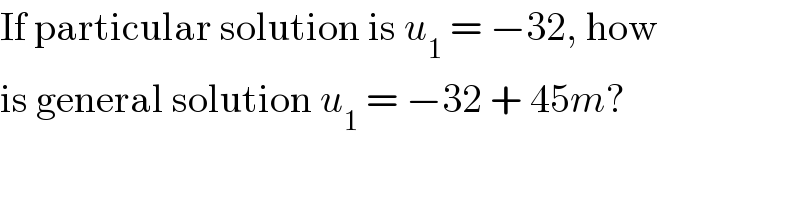
If particular solution is u_1 = −32, how is general solution u_1 = −32 + 45m?

$$\mathrm{If}\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{is}\:{u}_{\mathrm{1}} \:=\:−\mathrm{32},\:\mathrm{how} \\ $$ $$\mathrm{is}\:\mathrm{general}\:\mathrm{solution}\:{u}_{\mathrm{1}} \:=\:−\mathrm{32}\:+\:\mathrm{45}{m}? \\ $$

Commented bymrW1 last updated on 13/Aug/17

This is the basic to solve such questions. let′s have a look at ax+by=c. let′s say the greates common divisor of a and b is δ, i.e. δ=gcd(a,b). we see that a solution exists if and only if δ is a divisor of c. then: ax+by=c⇔(a/δ)x+(b/δ)y=(c/δ) or we write it as a′x+b′y=c′ with a′=(a/δ), etc. a′ and b′ are relatively prime and a′x+b′y=c′ has always solution. if a′x+b′y=c′ has a particular solution x_1 and y_1 , i.e. a′x_1 +b′y_1 =c′, then its general solution can be expressed as: x=x_1 +b′n y=y_1 −a′n (with n=any integer) this can be easily checked: a′(x_1 +b′n)+b′(y_1 −a′n) =a′x_1 +a′b′n+b′y_1 −b′a′n =a′x_1 +b′y_1 =c′ certainly you can also write the general solution as x=x_1 −b′n y=y_1 +a′n but this makes no difference since n can be any integer value. now we go back to your question. 7u+45z=1 δ=gcd(a,b)=gcd(7,45)=1 ⇒a′=7, b′=45, c′=1 7u+45z=1 has a particular solution: u_1 =−32 and z_1 =5 according to above its general solution is u=u_1 +b′m=−32+45m (or −32−45m) z=z_1 −a′m=5−7m (or 5+7m) I hope I could explain clearly enough.

$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{basic}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{such}\:\mathrm{questions}. \\ $$ $$ \\ $$ $$\mathrm{let}'\mathrm{s}\:\mathrm{have}\:\mathrm{a}\:\mathrm{look}\:\mathrm{at}\:\mathrm{ax}+\mathrm{by}=\mathrm{c}. \\ $$ $$ \\ $$ $$\mathrm{let}'\mathrm{s}\:\mathrm{say}\:\mathrm{the}\:\mathrm{greates}\:\mathrm{common}\:\mathrm{divisor} \\ $$ $$\mathrm{of}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{is}\:\delta,\:\mathrm{i}.\mathrm{e}.\:\delta=\mathrm{gcd}\left(\mathrm{a},\mathrm{b}\right). \\ $$ $$\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{exists}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$ $$\delta\:\mathrm{is}\:\mathrm{a}\:\mathrm{divisor}\:\mathrm{of}\:\mathrm{c}.\:\mathrm{then}: \\ $$ $$\mathrm{ax}+\mathrm{by}=\mathrm{c}\Leftrightarrow\frac{\mathrm{a}}{\delta}\mathrm{x}+\frac{\mathrm{b}}{\delta}\mathrm{y}=\frac{\mathrm{c}}{\delta} \\ $$ $$\mathrm{or}\:\mathrm{we}\:\mathrm{write}\:\mathrm{it}\:\mathrm{as}\:\mathrm{a}'\mathrm{x}+\mathrm{b}'\mathrm{y}=\mathrm{c}'\:\mathrm{with}\:\mathrm{a}'=\frac{\mathrm{a}}{\delta},\:\mathrm{etc}. \\ $$ $$\mathrm{a}'\:\mathrm{and}\:\mathrm{b}'\:\mathrm{are}\:\mathrm{relatively}\:\mathrm{prime}\:\mathrm{and} \\ $$ $$\mathrm{a}'\mathrm{x}+\mathrm{b}'\mathrm{y}=\mathrm{c}'\:\mathrm{has}\:\mathrm{always}\:\mathrm{solution}. \\ $$ $$ \\ $$ $$\mathrm{if}\:\mathrm{a}'\mathrm{x}+\mathrm{b}'\mathrm{y}=\mathrm{c}'\:\mathrm{has}\:\mathrm{a}\:\mathrm{particular}\:\mathrm{solution} \\ $$ $$\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{y}_{\mathrm{1}} ,\:\mathrm{i}.\mathrm{e}.\:\mathrm{a}'\mathrm{x}_{\mathrm{1}} +\mathrm{b}'\mathrm{y}_{\mathrm{1}} =\mathrm{c}',\:\mathrm{then} \\ $$ $$\mathrm{its}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{can}\:\mathrm{be}\:\mathrm{expressed}\:\mathrm{as}: \\ $$ $$\mathrm{x}=\mathrm{x}_{\mathrm{1}} +\mathrm{b}'\mathrm{n} \\ $$ $$\mathrm{y}=\mathrm{y}_{\mathrm{1}} −\mathrm{a}'\mathrm{n}\:\left(\mathrm{with}\:\mathrm{n}=\mathrm{any}\:\mathrm{integer}\right) \\ $$ $$ \\ $$ $$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{easily}\:\mathrm{checked}: \\ $$ $$\mathrm{a}'\left(\mathrm{x}_{\mathrm{1}} +\mathrm{b}'\mathrm{n}\right)+\mathrm{b}'\left(\mathrm{y}_{\mathrm{1}} −\mathrm{a}'\mathrm{n}\right) \\ $$ $$=\mathrm{a}'\mathrm{x}_{\mathrm{1}} +\mathrm{a}'\mathrm{b}'\mathrm{n}+\mathrm{b}'\mathrm{y}_{\mathrm{1}} −\mathrm{b}'\mathrm{a}'\mathrm{n} \\ $$ $$=\mathrm{a}'\mathrm{x}_{\mathrm{1}} +\mathrm{b}'\mathrm{y}_{\mathrm{1}} \\ $$ $$=\mathrm{c}' \\ $$ $$\mathrm{certainly}\:\mathrm{you}\:\mathrm{can}\:\mathrm{also}\:\mathrm{write}\:\mathrm{the} \\ $$ $$\mathrm{general}\:\mathrm{solution}\:\mathrm{as} \\ $$ $$\mathrm{x}=\mathrm{x}_{\mathrm{1}} −\mathrm{b}'\mathrm{n} \\ $$ $$\mathrm{y}=\mathrm{y}_{\mathrm{1}} +\mathrm{a}'\mathrm{n} \\ $$ $$\mathrm{but}\:\mathrm{this}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{difference}\:\mathrm{since}\:\mathrm{n}\:\mathrm{can} \\ $$ $$\mathrm{be}\:\mathrm{any}\:\mathrm{integer}\:\mathrm{value}. \\ $$ $$ \\ $$ $$\mathrm{now}\:\mathrm{we}\:\mathrm{go}\:\mathrm{back}\:\mathrm{to}\:\mathrm{your}\:\mathrm{question}. \\ $$ $$\mathrm{7u}+\mathrm{45z}=\mathrm{1} \\ $$ $$\delta=\mathrm{gcd}\left(\mathrm{a},\mathrm{b}\right)=\mathrm{gcd}\left(\mathrm{7},\mathrm{45}\right)=\mathrm{1} \\ $$ $$\Rightarrow\mathrm{a}'=\mathrm{7},\:\mathrm{b}'=\mathrm{45},\:\mathrm{c}'=\mathrm{1} \\ $$ $$\mathrm{7u}+\mathrm{45z}=\mathrm{1}\:\mathrm{has}\:\mathrm{a}\:\mathrm{particular}\:\mathrm{solution}: \\ $$ $$\mathrm{u}_{\mathrm{1}} =−\mathrm{32}\:\mathrm{and}\:\mathrm{z}_{\mathrm{1}} =\mathrm{5} \\ $$ $$\mathrm{according}\:\mathrm{to}\:\mathrm{above}\:\mathrm{its}\:\mathrm{general}\:\mathrm{solution} \\ $$ $$\mathrm{is} \\ $$ $$\mathrm{u}=\mathrm{u}_{\mathrm{1}} +\mathrm{b}'\mathrm{m}=−\mathrm{32}+\mathrm{45m}\:\left(\mathrm{or}\:−\mathrm{32}−\mathrm{45m}\right) \\ $$ $$\mathrm{z}=\mathrm{z}_{\mathrm{1}} −\mathrm{a}'\mathrm{m}=\mathrm{5}−\mathrm{7m}\:\left(\mathrm{or}\:\mathrm{5}+\mathrm{7m}\right) \\ $$ $$ \\ $$ $$\mathrm{I}\:\mathrm{hope}\:\mathrm{I}\:\mathrm{could}\:\mathrm{explain}\:\mathrm{clearly}\:\mathrm{enough}. \\ $$

Commented byTinkutara last updated on 13/Aug/17

Thank you very much Sir! This explanation is very useful.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}!\:\mathrm{This} \\ $$ $$\mathrm{explanation}\:\mathrm{is}\:\mathrm{very}\:\mathrm{useful}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com