Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19349 by Tinkutara last updated on 10/Aug/17

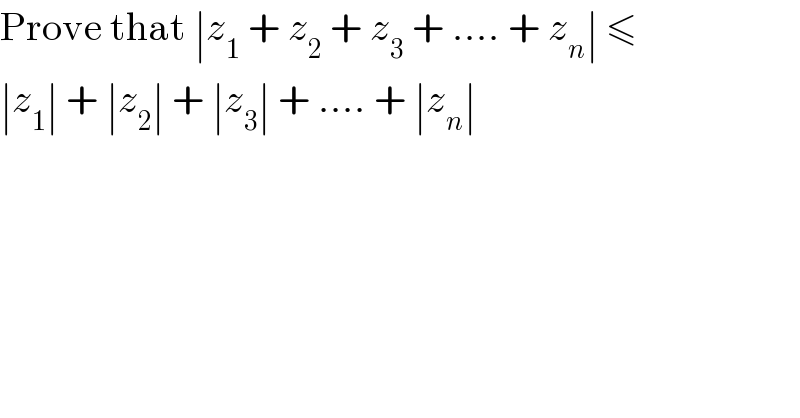
Prove that ∣z_1 + z_2 + z_3 + .... + z_n ∣ ≤ ∣z_1 ∣ + ∣z_2 ∣ + ∣z_3 ∣ + .... + ∣z_n ∣

$$\mathrm{Prove}\:\mathrm{that}\:\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \:+\:{z}_{\mathrm{3}} \:+\:....\:+\:{z}_{{n}} \mid\:\leqslant \\ $$$$\mid{z}_{\mathrm{1}} \mid\:+\:\mid{z}_{\mathrm{2}} \mid\:+\:\mid{z}_{\mathrm{3}} \mid\:+\:....\:+\:\mid{z}_{{n}} \mid \\ $$

Commented by Tinkutara last updated on 10/Aug/17

I have this proof in my book but I have a doubt in that proof. Can anyone explain this? Why only r_1 is multiplied with all other r_2 , r_3 , .... r_n ? Why all these are not multiplied with each other?

$$\mathrm{I}\:\mathrm{have}\:\mathrm{this}\:\mathrm{proof}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book}\:\mathrm{but}\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{a}\:\mathrm{doubt}\:\mathrm{in}\:\mathrm{that}\:\mathrm{proof}.\:\mathrm{Can}\:\mathrm{anyone} \\ $$$$\mathrm{explain}\:\mathrm{this}?\:\mathrm{Why}\:\mathrm{only}\:{r}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{multiplied} \\ $$$$\mathrm{with}\:\mathrm{all}\:\mathrm{other}\:{r}_{\mathrm{2}} ,\:{r}_{\mathrm{3}} ,\:....\:{r}_{{n}} ?\:\mathrm{Why}\:\mathrm{all} \\ $$$$\mathrm{these}\:\mathrm{are}\:\mathrm{not}\:\mathrm{multiplied}\:\mathrm{with}\:\mathrm{each} \\ $$$$\mathrm{other}? \\ $$

Commented by Tinkutara last updated on 10/Aug/17

Answered by mrW1 last updated on 11/Aug/17

z_1 =a_1 +b_1 i z_2 =a_2 +b_2 i ∣z_1 +z_2 ∣=(√((a_1 +a_2 )^2 +(b_1 +b_2 )^2 )) ∣z_1 ∣=(√(a_1 ^2 +b_1 ^2 )) ∣z_2 ∣=(√(a_2 ^2 +b_2 ^2 )) ∣z_1 ∣+∣z_2 ∣=(√(a_1 ^2 +b_1 ^2 ))+(√(a_2 ^2 +b_2 ^2 )) since (√((a_1 +a_2 )^2 +(b_1 +b_2 )^2 ))≤(√(a_1 ^2 +b_1 ^2 ))+(√(a_2 ^2 +b_2 ^2 )) (see below) ⇒∣z_1 +z_2 ∣≤∣z_1 ∣+∣z_2 ∣ ∣z_1 + z_2 + z_3 + .... + z_n ∣ ≤∣z_1 ∣ +∣z_2 + z_3 + .... + z_n ∣ ≤∣z_1 ∣ +∣z_2 ∣ + ∣z_3 + .... + z_n ∣ ...... ≤∣z_1 ∣ +∣z_2 ∣ + ∣z_3 ∣ + .... + ∣z_n ∣

$$\mathrm{z}_{\mathrm{1}} =\mathrm{a}_{\mathrm{1}} +\mathrm{b}_{\mathrm{1}} \mathrm{i} \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{a}_{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} \mathrm{i} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} \mid=\sqrt{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}_{\mathrm{1}} +\mathrm{b}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid=\sqrt{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$$\mid\mathrm{z}_{\mathrm{2}} \mid=\sqrt{\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid+\mid\mathrm{z}_{\mathrm{2}} \mid=\sqrt{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} ^{\mathrm{2}} }+\sqrt{\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\mathrm{since}\:\sqrt{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}_{\mathrm{1}} +\mathrm{b}_{\mathrm{2}} \right)^{\mathrm{2}} }\leqslant\sqrt{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} ^{\mathrm{2}} }+\sqrt{\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} ^{\mathrm{2}} }\:\left(\mathrm{see}\:\mathrm{below}\right) \\ $$$$\Rightarrow\mid\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} \mid\leqslant\mid\mathrm{z}_{\mathrm{1}} \mid+\mid\mathrm{z}_{\mathrm{2}} \mid \\ $$$$ \\ $$$$\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \:+\:{z}_{\mathrm{3}} \:+\:....\:+\:{z}_{{n}} \mid\: \\ $$$$\leqslant\mid{z}_{\mathrm{1}} \mid\:+\mid{z}_{\mathrm{2}} \:+\:{z}_{\mathrm{3}} \:+\:....\:+\:{z}_{{n}} \mid\: \\ $$$$\leqslant\mid{z}_{\mathrm{1}} \mid\:+\mid{z}_{\mathrm{2}} \mid\:+\:\mid{z}_{\mathrm{3}} \:+\:....\:+\:{z}_{{n}} \mid\: \\ $$$$...... \\ $$$$\leqslant\mid{z}_{\mathrm{1}} \mid\:+\mid{z}_{\mathrm{2}} \mid\:+\:\mid{z}_{\mathrm{3}} \mid\:+\:....\:+\:\mid{z}_{{n}} \mid\: \\ $$

Commented by mrW1 last updated on 11/Aug/17

Commented by mrW1 last updated on 11/Aug/17

AB=(√(a_1 ^2 +b_1 ^2 )) BC=(√(a_2 ^2 +b_2 ^2 )) AC=(√((a_1 +a_2 )^2 +(b_1 +b_2 )^2 )) since AC≤AB+BC (√((a_1 +a_2 )^2 +(b_1 +b_2 )^2 ))≤(√(a_1 ^2 +b_1 ^2 ))+(√(a_2 ^2 +b_2 ^2 ))

$$\mathrm{AB}=\sqrt{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} ^{\mathrm{2}} } \\ $$$$\mathrm{BC}=\sqrt{\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\mathrm{AC}=\sqrt{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}_{\mathrm{1}} +\mathrm{b}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{since}\:\mathrm{AC}\leqslant\mathrm{AB}+\mathrm{BC} \\ $$$$\sqrt{\left(\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}_{\mathrm{1}} +\mathrm{b}_{\mathrm{2}} \right)^{\mathrm{2}} }\leqslant\sqrt{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} ^{\mathrm{2}} }+\sqrt{\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$

Commented by Tinkutara last updated on 12/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com