Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19351 by Tinkutara last updated on 10/Aug/17

Prove that ∣z_1 + z_2 ∣^2 = ∣z_1 ∣^2 + ∣z_2 ∣^2 ⇔ (z_1 /z_2 ) is purely imaginary number.

$$\mathrm{Prove}\:\mathrm{that}\:\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:=\:\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} \:+\:\mid{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\:\mathrm{is}\:\mathrm{purely}\:\mathrm{imaginary}\:\mathrm{number}. \\ $$

Commented by dioph last updated on 10/Aug/17

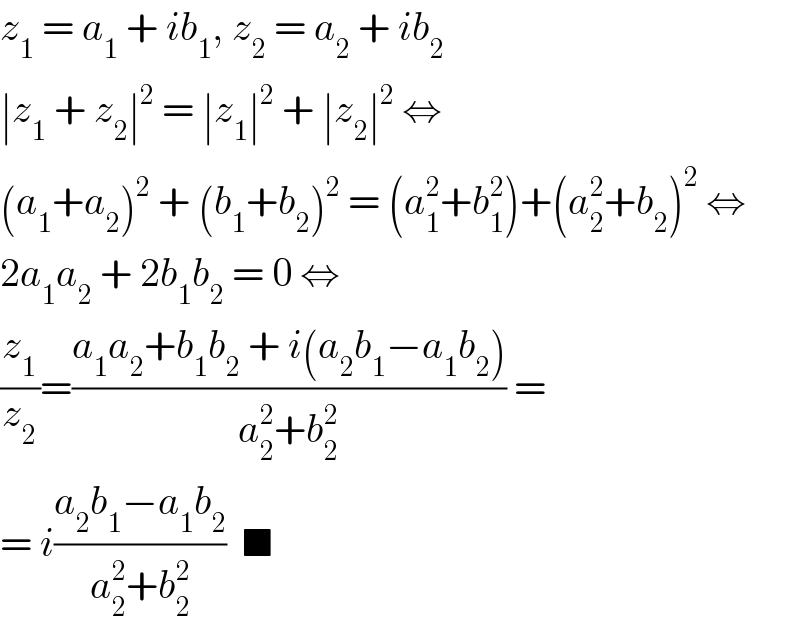
z_1 = a_1 + ib_1 , z_2 = a_2 + ib_2 ∣z_1 + z_2 ∣^2 = ∣z_1 ∣^2 + ∣z_2 ∣^2 ⇔ (a_1 +a_2 )^2 + (b_1 +b_2 )^2 = (a_1 ^2 +b_1 ^2 )+(a_2 ^2 +b_2 )^2 ⇔ 2a_1 a_2 + 2b_1 b_2 = 0 ⇔ (z_1 /z_2 )=((a_1 a_2 +b_1 b_2 + i(a_2 b_1 −a_1 b_2 ))/(a_2 ^2 +b_2 ^2 )) = = i((a_2 b_1 −a_1 b_2 )/(a_2 ^2 +b_2 ^2 )) ■

$${z}_{\mathrm{1}} \:=\:{a}_{\mathrm{1}} \:+\:{ib}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} \:=\:{a}_{\mathrm{2}} \:+\:{ib}_{\mathrm{2}} \\ $$$$\mid{z}_{\mathrm{1}} \:+\:{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:=\:\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} \:+\:\mid{z}_{\mathrm{2}} \mid^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\left({a}_{\mathrm{1}} +{a}_{\mathrm{2}} \right)^{\mathrm{2}} \:+\:\left({b}_{\mathrm{1}} +{b}_{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\left({a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} \right)+\left({a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} \right)^{\mathrm{2}} \:\Leftrightarrow \\ $$$$\mathrm{2}{a}_{\mathrm{1}} {a}_{\mathrm{2}} \:+\:\mathrm{2}{b}_{\mathrm{1}} {b}_{\mathrm{2}} \:=\:\mathrm{0}\:\Leftrightarrow \\ $$$$\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }=\frac{{a}_{\mathrm{1}} {a}_{\mathrm{2}} +{b}_{\mathrm{1}} {b}_{\mathrm{2}} \:+\:{i}\left({a}_{\mathrm{2}} {b}_{\mathrm{1}} −{a}_{\mathrm{1}} {b}_{\mathrm{2}} \right)}{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} }\:= \\ $$$$=\:{i}\frac{{a}_{\mathrm{2}} {b}_{\mathrm{1}} −{a}_{\mathrm{1}} {b}_{\mathrm{2}} }{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\blacksquare \\ $$

Commented by Tinkutara last updated on 10/Aug/17

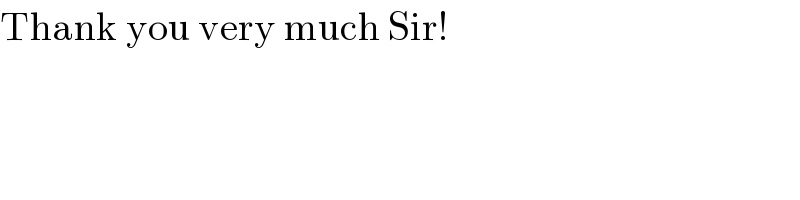
Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by ajfour last updated on 10/Aug/17

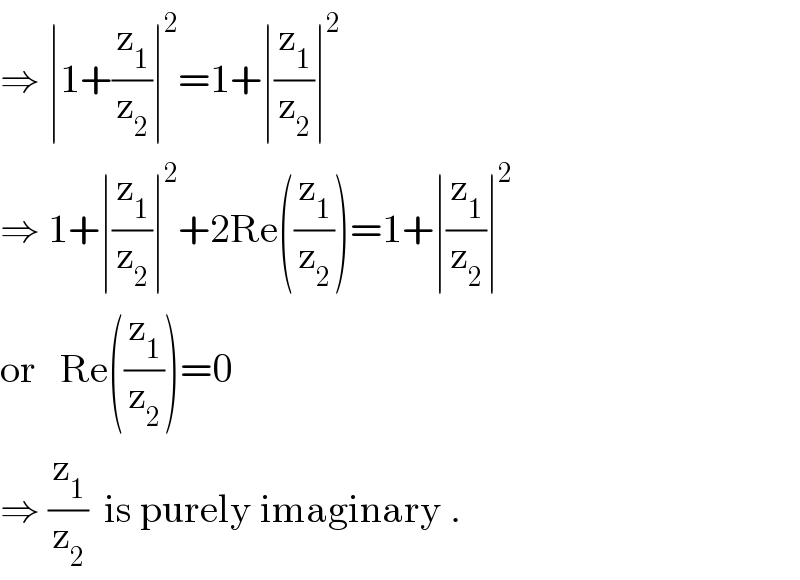
⇒ ∣1+(z_1 /z_2 )∣^2 =1+∣(z_1 /z_2 )∣^2 ⇒ 1+∣(z_1 /z_2 )∣^2 +2Re((z_1 /z_2 ))=1+∣(z_1 /z_2 )∣^2 or Re((z_1 /z_2 ))=0 ⇒ (z_1 /z_2 ) is purely imaginary .

$$\Rightarrow\:\mid\mathrm{1}+\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} =\mathrm{1}+\mid\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{1}+\mid\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} +\mathrm{2Re}\left(\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\right)=\mathrm{1}+\mid\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\mid^{\mathrm{2}} \\ $$$$\mathrm{or}\:\:\:\mathrm{Re}\left(\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\right)=\mathrm{0}\:\: \\ $$$$\Rightarrow\:\frac{\mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{2}} }\:\:\mathrm{is}\:\mathrm{purely}\:\mathrm{imaginary}\:. \\ $$

Commented by Tinkutara last updated on 10/Aug/17

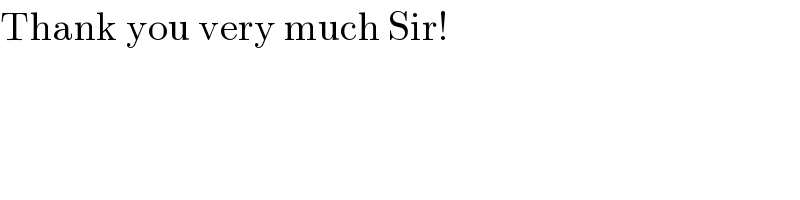
Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com