Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19403 by Tinkutara last updated on 10/Aug/17

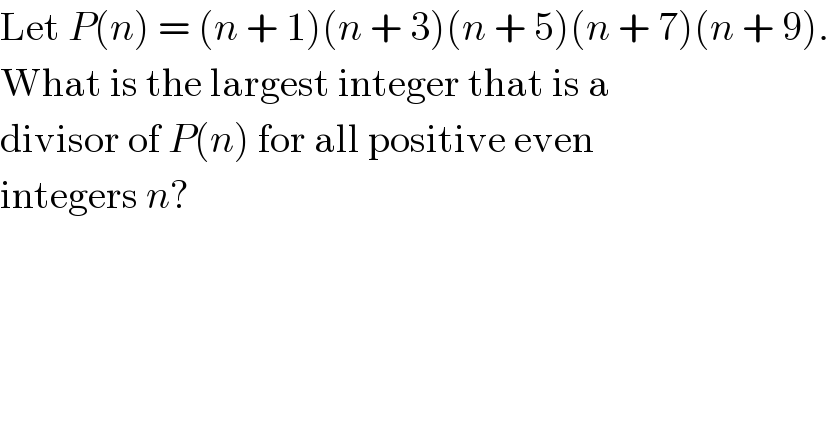
Let P(n) = (n + 1)(n + 3)(n + 5)(n + 7)(n + 9). What is the largest integer that is a divisor of P(n) for all positive even integers n?

$$\mathrm{Let}\:{P}\left({n}\right)\:=\:\left({n}\:+\:\mathrm{1}\right)\left({n}\:+\:\mathrm{3}\right)\left({n}\:+\:\mathrm{5}\right)\left({n}\:+\:\mathrm{7}\right)\left({n}\:+\:\mathrm{9}\right). \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{integer}\:\mathrm{that}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{divisor}\:\mathrm{of}\:{P}\left({n}\right)\:\mathrm{for}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{even} \\ $$$$\mathrm{integers}\:{n}? \\ $$

Commented by RasheedSindhi last updated on 12/Aug/17

15

$$\mathrm{15} \\ $$

Answered by RasheedSindhi last updated on 12/Aug/17

P(n)=(n+1)(n+3)(n+5)(n+7)(n+9) n∈E^+ ;Let n=2m,m∈N P(2m)=(2m+1)(2m+3)(2m+5)(2m+7)(2m+9) m=3k∣m=3k+1∣m=3k+2 C-0 : m=3k⇒ P(n)=P(2m)=P(2.3k) =(6k+1)(6k+3)(6k+5)(6k+7)(6k+9) =3(6k+1)(2k+1)(6k+5)(6k+7)(6k+9) C-1 : m=3k+1⇒ P(n)=(6k+3)(6k+5)(6k+7)(6k+9)(6k+11) =9(2k+1)(6k+5)(6k+7)(2k+3)(6k+11) C-2 : m=3k+2⇒ P(n)=(6k+5)(6k+7)(6k+9)(6k+11)(6k+13) =3(6k+5)(6k+7)(2k+3)(6k+11)(6k+13) In all the three cases: 3 ∣ P(n) Similarly we can prove that 5 ∣ P(n) Also can be verified from P(10) that 3 and 5 can divide P(n) once only. P(10)=11.13.15.17.19 =11.13.3.5.17.19 From the following it is proved that there isn′t any divisor of P(n) other than 3 & 5 P(2)=3.5.7.9.11 P(10)=11.13.15.17.19 P(12)=13.15.17.19.21 Hence the largest divisor is 3×5=15

$$\mathrm{P}\left(\mathrm{n}\right)=\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{5}\right)\left(\mathrm{n}+\mathrm{7}\right)\left(\mathrm{n}+\mathrm{9}\right) \\ $$$$\mathrm{n}\in\mathbb{E}^{+} ;\mathrm{Let}\:\mathrm{n}=\mathrm{2m},\mathrm{m}\in\mathbb{N} \\ $$$$\mathrm{P}\left(\mathrm{2m}\right)=\left(\mathrm{2m}+\mathrm{1}\right)\left(\mathrm{2m}+\mathrm{3}\right)\left(\mathrm{2m}+\mathrm{5}\right)\left(\mathrm{2m}+\mathrm{7}\right)\left(\mathrm{2m}+\mathrm{9}\right) \\ $$$$\mathrm{m}=\mathrm{3k}\mid\mathrm{m}=\mathrm{3k}+\mathrm{1}\mid\mathrm{m}=\mathrm{3k}+\mathrm{2} \\ $$$$\mathrm{C}-\mathrm{0}\::\:\mathrm{m}=\mathrm{3k}\Rightarrow \\ $$$$\mathrm{P}\left(\mathrm{n}\right)=\mathrm{P}\left(\mathrm{2m}\right)=\mathrm{P}\left(\mathrm{2}.\mathrm{3k}\right) \\ $$$$=\left(\mathrm{6k}+\mathrm{1}\right)\left(\mathrm{6k}+\mathrm{3}\right)\left(\mathrm{6k}+\mathrm{5}\right)\left(\mathrm{6k}+\mathrm{7}\right)\left(\mathrm{6k}+\mathrm{9}\right) \\ $$$$\:\:=\mathrm{3}\left(\mathrm{6k}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{1}\right)\left(\mathrm{6k}+\mathrm{5}\right)\left(\mathrm{6k}+\mathrm{7}\right)\left(\mathrm{6k}+\mathrm{9}\right) \\ $$$$\mathrm{C}-\mathrm{1}\::\:\mathrm{m}=\mathrm{3k}+\mathrm{1}\Rightarrow \\ $$$$\mathrm{P}\left(\mathrm{n}\right)=\left(\mathrm{6k}+\mathrm{3}\right)\left(\mathrm{6k}+\mathrm{5}\right)\left(\mathrm{6k}+\mathrm{7}\right)\left(\mathrm{6k}+\mathrm{9}\right)\left(\mathrm{6k}+\mathrm{11}\right) \\ $$$$\:\:=\mathrm{9}\left(\mathrm{2k}+\mathrm{1}\right)\left(\mathrm{6k}+\mathrm{5}\right)\left(\mathrm{6k}+\mathrm{7}\right)\left(\mathrm{2k}+\mathrm{3}\right)\left(\mathrm{6k}+\mathrm{11}\right) \\ $$$$\mathrm{C}-\mathrm{2}\::\:\mathrm{m}=\mathrm{3k}+\mathrm{2}\Rightarrow \\ $$$$\mathrm{P}\left(\mathrm{n}\right)=\left(\mathrm{6k}+\mathrm{5}\right)\left(\mathrm{6k}+\mathrm{7}\right)\left(\mathrm{6k}+\mathrm{9}\right)\left(\mathrm{6k}+\mathrm{11}\right)\left(\mathrm{6k}+\mathrm{13}\right) \\ $$$$\:\:=\mathrm{3}\left(\mathrm{6k}+\mathrm{5}\right)\left(\mathrm{6k}+\mathrm{7}\right)\left(\mathrm{2k}+\mathrm{3}\right)\left(\mathrm{6k}+\mathrm{11}\right)\left(\mathrm{6k}+\mathrm{13}\right) \\ $$$$\:\mathrm{In}\:\mathrm{all}\:\mathrm{the}\:\mathrm{three}\:\mathrm{cases}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\mid\:\mathrm{P}\left(\mathrm{n}\right) \\ $$$$\mathrm{Similarly}\:\mathrm{we}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}\:\mid\:\mathrm{P}\left(\mathrm{n}\right) \\ $$$$\mathrm{Also}\:\mathrm{can}\:\mathrm{be}\:\mathrm{verified}\:\mathrm{from}\:\mathrm{P}\left(\mathrm{10}\right) \\ $$$$\mathrm{that}\:\mathrm{3}\:\mathrm{and}\:\mathrm{5}\:\mathrm{can}\:\mathrm{divide}\:\mathrm{P}\left(\mathrm{n}\right)\:\mathrm{once}\:\mathrm{only}. \\ $$$$\mathrm{P}\left(\mathrm{10}\right)=\mathrm{11}.\mathrm{13}.\mathrm{15}.\mathrm{17}.\mathrm{19} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{11}.\mathrm{13}.\mathrm{3}.\mathrm{5}.\mathrm{17}.\mathrm{19} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{following}\:\mathrm{it}\:\mathrm{is}\:\mathrm{proved} \\ $$$$\mathrm{that}\:\:\mathrm{there}\:\mathrm{isn}'\mathrm{t}\:\mathrm{any}\:\mathrm{divisor}\:\mathrm{of}\:\mathrm{P}\left(\mathrm{n}\right) \\ $$$$\mathrm{other}\:\mathrm{than}\:\mathrm{3}\:\&\:\mathrm{5} \\ $$$$\mathrm{P}\left(\mathrm{2}\right)=\mathrm{3}.\mathrm{5}.\mathrm{7}.\mathrm{9}.\mathrm{11} \\ $$$$\mathrm{P}\left(\mathrm{10}\right)=\mathrm{11}.\mathrm{13}.\mathrm{15}.\mathrm{17}.\mathrm{19} \\ $$$$\mathrm{P}\left(\mathrm{12}\right)=\mathrm{13}.\mathrm{15}.\mathrm{17}.\mathrm{19}.\mathrm{21} \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{divisor}\:\mathrm{is} \\ $$$$\mathrm{3}×\mathrm{5}=\mathrm{15} \\ $$

Commented by Tinkutara last updated on 12/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com