f(xf(y)+x)=xy+f(x) f:R→R f(x)=?


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 198178 by universe last updated on 13/Oct/23

$f (x f (y) + x) = x y + f (x)$ $f : R \to R$ $f (x) = ?$
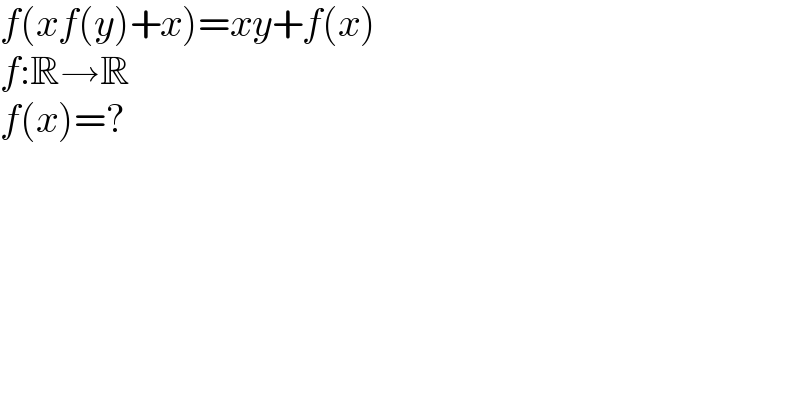
	Answered by Rasheed.Sindhi last updated on 13/Oct/23

	$L e t f (x) = a x + b$ $f (x f (y) + x) = x y + f (x)$ $\Rightarrow a (x f (y) + x) + b = x y + a x + b$ $\Rightarrow a x (a y + b) + a x = x y + a x$ $\Rightarrow a x (a y + b) = x y$ $y \to x$ $\Rightarrow a x (a x + b) = x^{2}$ $a^{2} x^{2} + b x = x^{2}$ $a^{2} = 1 \land b = 0$ $a = \pm 1 \land b = 0$ $f (x) = a x + b = (\pm 1) x + 0$ $\begin{matrix} \begin{matrix} f (x) = x ∣ f (x) = - x \end{matrix} \end{matrix}$ $V e r i f i c a t i o n :$ $(1) f (x) = x$ $f (x f (y) + x) = x y + f (x)$ $x f (y) + x = x y + f (x)$ $\Rightarrow x y + x = x y + x (✓)$ $(2) f (x) = - x$ $f (x f (y) + x) = x y + f (x)$ $\Rightarrow - x f (y) - x = x y - x$ $\Rightarrow - x f (y) - x = x y - x$ $\Rightarrow - x (- y) - x = x y - x$ $\Rightarrow x y - x = x y - x (✓)$
	Commented by mr W last updated on 13/Oct/23

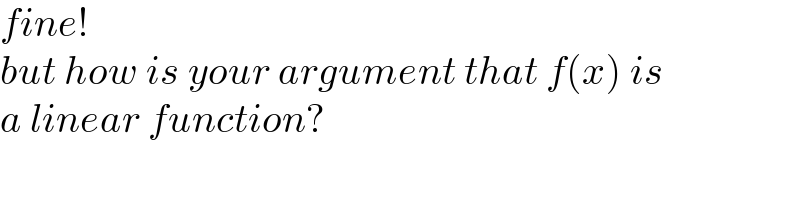
	$f i n e!$ $b u t h o w i s y o u r a r g u m e n t t h a t f (x) i s$ $a l i n e a r f u n c t i o n ?$
	Commented by Rasheed.Sindhi last updated on 13/Oct/23

	$s i r, I^{'} v e n o a r g u m e n t! E v e n a b o u t$ $t h e f u n c t i o n t o b e p o l y n o m i a l! B u t {t h e r e}^{'} s$ $p o s s i b i l i t y o f b e i n g l i n e a r .$
	Answered by witcher3 last updated on 13/Oct/23
	$let b∈R ∃ t∈R∣f(t)=b.....? (x,y)=(1,y)⇒f(f(y)+1)=y+f(1) y=b−f(1) ⇒f(f(b−f(1)+1)=b,t=f(b−f(1))+1 f surjective if f(a)=f(b)⇒(a=b)...? (x,y)=(1,y) f(f(y)+1)=y+f(1)..y=a y=b⇒a=b ⇒ f is injective so f bijective f(f(y)+1)=y+f(1) for y=0⇒f(f(0)+1)=f(1) withe injectivity⇒f(0)+1=1⇒f(0)=0 ∀t∈R−{0}⇔f(t)≠0 by bijection“ (x,y)=(x,y^∗ ),suche f(y^∗ )=−1.y^∗ existe f surjective ⇔f(x.−1+x)=xy^∗ +f(x)=f(0)=0 f(x)=−xy^∗ f is linear f(x)=ax solution⇒(x,y)=(x,x) f(ax^2 +x)=a^2 x^2 +ax=x^2 +ax⇒a^2 =1 a∈{−1,1} ∀(x,y)∈R^2 ∣f(xf(y)+x)=xy+f(x)⇒f∈{f(x)=x,f(x)=−x}$
	$let b \in R \exists t \in R ∣ f (t) = b . . . . . ?$ $(x, y) = (1, y) \Rightarrow f (f (y) + 1) = y + f (1)$ $y = b - f (1)$ $\Rightarrow f (f (b - f (1) + 1) = b, t = f (b - f (1)) + 1$ $f surjective$ $if f (a) = f (b) \Rightarrow (a = b) . . . ?$ $(x, y) = (1, y)$ $f (f (y) + 1) = y + f (1) . . y = a y = b \Rightarrow a = b$ $\Rightarrow f is injective$ $so f bijective$ $f (f (y) + 1) = y + f (1) for y = 0 \Rightarrow f (f (0) + 1) = f (1)$ $withe injectivity \Rightarrow f (0) + 1 = 1 \Rightarrow f (0) = 0$ $\forall t \in R - {0} \Leftrightarrow f (t) \neq 0 by bijection ‘ ‘$ $(x, y) = (x, \overset{}{y}), suche f (\overset{}{y}) = - 1 . \overset{}{y} existe f surjective$ $\Leftrightarrow f (x . - 1 + x) = x \overset{}{y} + f (x) = f (0) = 0$ $f (x) = - x \overset{*}{y}$ $f is linear$ $f (x) = ax solution \Rightarrow (x, y) = (x, x)$ $f ({ax}^{2} + x) = a^{2} x^{2} + ax = x^{2} + ax \Rightarrow a^{2} = 1$ $a \in {- 1, 1}$ $\forall (x, y) \in R^{2} ∣ f (xf (y) + x) = xy + f (x) \Rightarrow f \in {f (x) = x, f (x) = - x}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum