
Question and Answers Forum
Question Number 19920 by lidaye last updated on 18/Aug/17
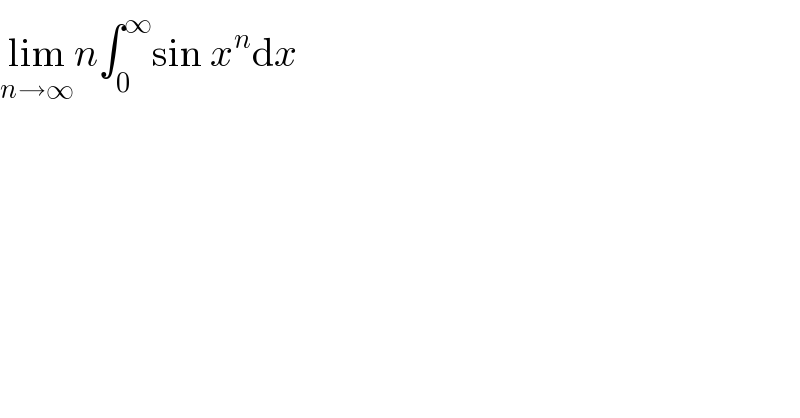
Commented by 1kanika# last updated on 18/Aug/17
Commented by prof Abdo imad last updated on 22/Jun/18
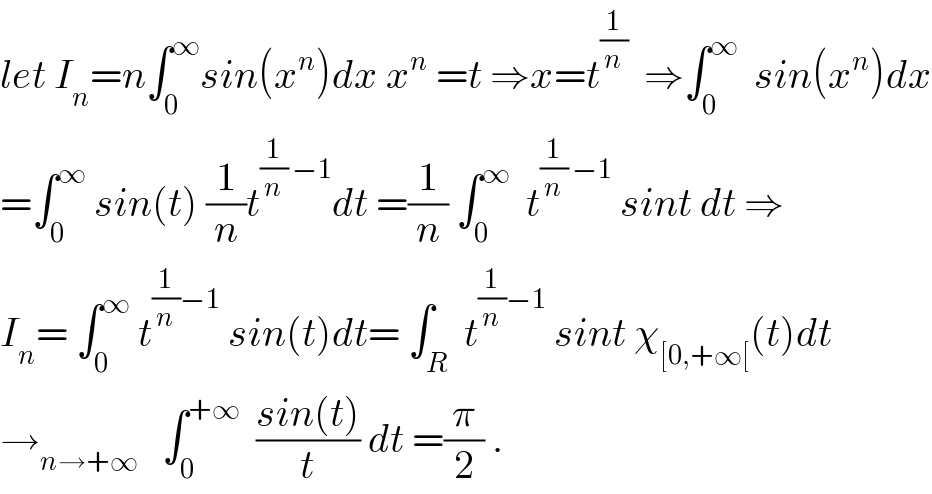
| ||
Question and Answers Forum | ||
Question Number 19920 by lidaye last updated on 18/Aug/17 | ||
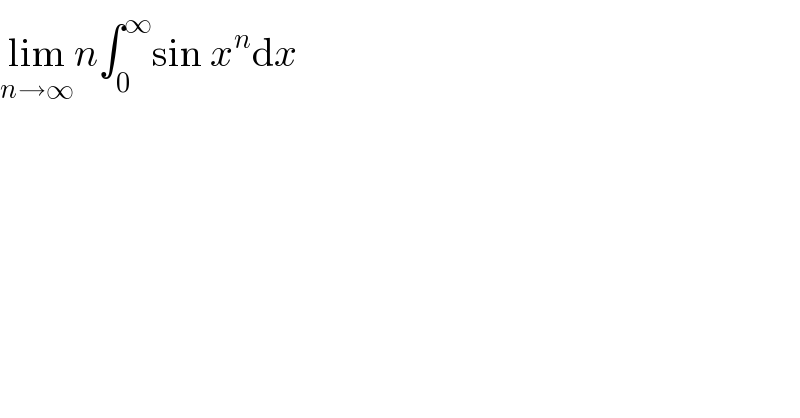 | ||
Commented by 1kanika# last updated on 18/Aug/17 | ||
 | ||
Commented by prof Abdo imad last updated on 22/Jun/18 | ||
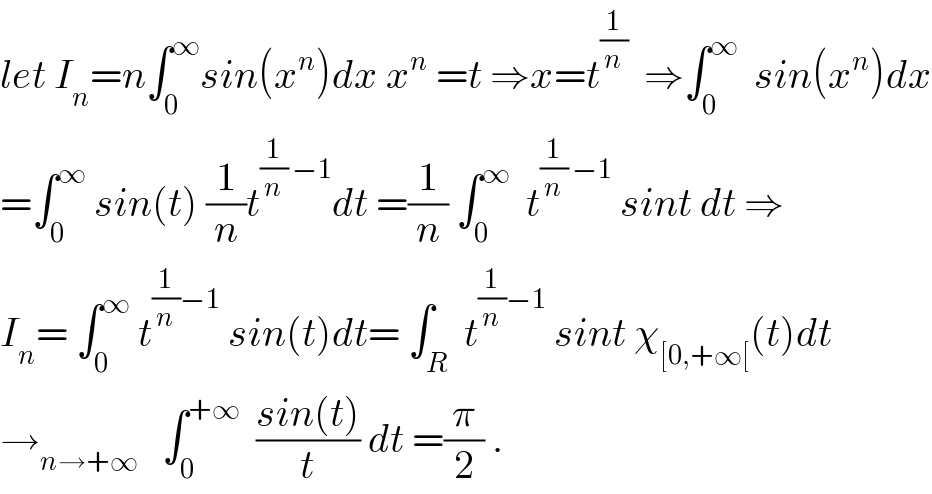 | ||