Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19945 by Tinkutara last updated on 18/Aug/17

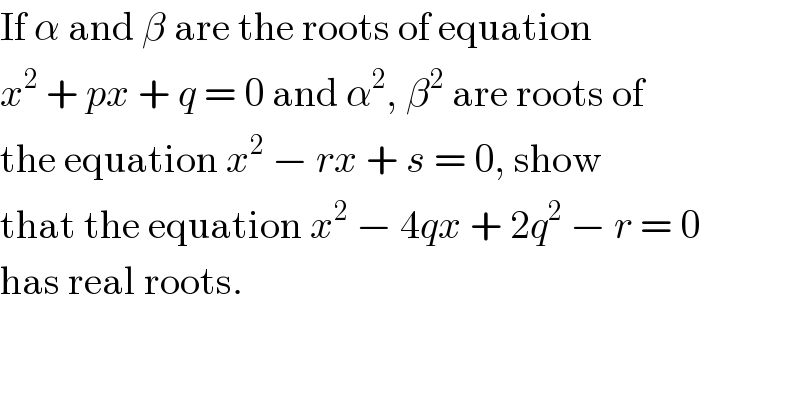
If α and β are the roots of equation x^2 + px + q = 0 and α^2 , β^2 are roots of the equation x^2 − rx + s = 0, show that the equation x^2 − 4qx + 2q^2 − r = 0 has real roots.

$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{equation} \\ $$$${x}^{\mathrm{2}} \:+\:{px}\:+\:{q}\:=\:\mathrm{0}\:\mathrm{and}\:\alpha^{\mathrm{2}} ,\:\beta^{\mathrm{2}} \:\mathrm{are}\:\mathrm{roots}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{equation}\:{x}^{\mathrm{2}} \:−\:{rx}\:+\:{s}\:=\:\mathrm{0},\:\mathrm{show} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:{x}^{\mathrm{2}} \:−\:\mathrm{4}{qx}\:+\:\mathrm{2}{q}^{\mathrm{2}} \:−\:{r}\:=\:\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{real}\:\mathrm{roots}. \\ $$

Answered by Rasheed.Sindhi last updated on 19/Aug/17

x^2 +px+q=0, roots:α,β (given) x^2 −rx+s=0, roots:α^2 ,β^2 (given) x^2 −4qx+2q^2 −r=0,roots are real.(to be proved) −−−−−−−−−−− α+β=−p ,αβ=q α^2 +β^2 =r,α^2 β^2 =s=q^2 x^2 −4qx+2q^2 −r=0 ⇒x^2 −4(αβ)x+2(αβ)^2 −(α^2 +β^2 )=0 x=((4αβ±(√(16α^2 β^2 −4(1)(2(αβ)^2 −(α^2 +β^2 )))))/2) x=((4αβ±2(√(4α^2 β^2 −2(αβ)^2 +(α^2 +β^2 ))))/2) =2αβ±(√(4α^2 β^2 −2α^2 β^2 +α^2 +β^2 )) =2αβ±(√(2α^2 β^2 +α^2 +β^2 )) α^2 ,β^2 ≥0⇒2α^2 β^2 +α^2 +β^2 ≥0 Hence the roots are real.

$$\mathrm{x}^{\mathrm{2}} +\mathrm{px}+\mathrm{q}=\mathrm{0},\:\mathrm{roots}:\alpha,\beta\:\left(\mathrm{given}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{rx}+\mathrm{s}=\mathrm{0},\:\mathrm{roots}:\alpha^{\mathrm{2}} ,\beta^{\mathrm{2}} \left(\mathrm{given}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4qx}+\mathrm{2q}^{\mathrm{2}} −\mathrm{r}=\mathrm{0},\mathrm{roots}\:\mathrm{are}\:\mathrm{real}.\left(\mathrm{to}\:\mathrm{be}\:\mathrm{proved}\right) \\ $$$$−−−−−−−−−−− \\ $$$$\alpha+\beta=−\mathrm{p}\:,\alpha\beta=\mathrm{q} \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\mathrm{r},\alpha^{\mathrm{2}} \beta^{\mathrm{2}} =\mathrm{s}=\mathrm{q}^{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4qx}+\mathrm{2q}^{\mathrm{2}} −\mathrm{r}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4}\left(\alpha\beta\right)\mathrm{x}+\mathrm{2}\left(\alpha\beta\right)^{\mathrm{2}} −\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\:\mathrm{x}=\frac{\mathrm{4}\alpha\beta\pm\sqrt{\mathrm{16}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{2}\left(\alpha\beta\right)^{\mathrm{2}} −\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\right)}}{\mathrm{2}} \\ $$$$\:\:\mathrm{x}=\frac{\mathrm{4}\alpha\beta\pm\mathrm{2}\sqrt{\mathrm{4}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} −\mathrm{2}\left(\alpha\beta\right)^{\mathrm{2}} +\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\:\:=\mathrm{2}\alpha\beta\pm\sqrt{\mathrm{4}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} −\mathrm{2}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} } \\ $$$$\:\:=\mathrm{2}\alpha\beta\pm\sqrt{\mathrm{2}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} } \\ $$$$\alpha^{\mathrm{2}} ,\beta^{\mathrm{2}} \geqslant\mathrm{0}\Rightarrow\mathrm{2}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{real}. \\ $$

Commented by Tinkutara last updated on 19/Aug/17

Thank you.

$$\mathrm{Thank}\:\mathrm{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com