
Question and Answers Forum
Question Number 101601 by Dwaipayan Shikari last updated on 03/Jul/20
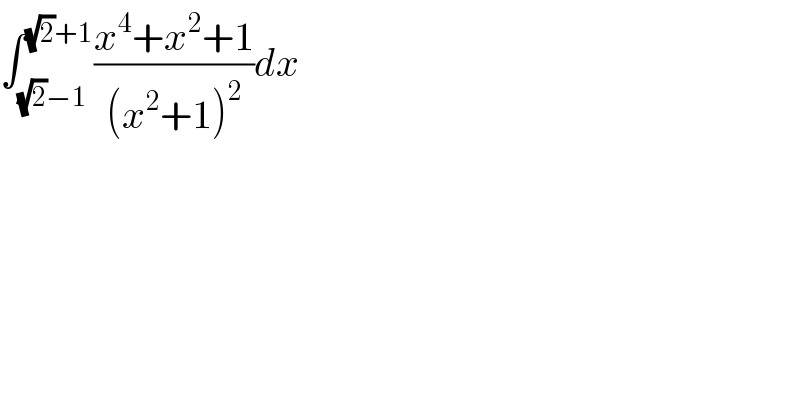
Answered by bemath last updated on 03/Jul/20
![∫ (((x^2 +1)^2 −x^2 )/((x^2 +1)^2 )) dx = x−∫ (x^2 /((x^2 +1)^2 )) dx I_2 = ∫ (x^2 /((x^2 +1)^2 )) dx [ x = tan p ] I_2 = ∫ ((tan^2 p . sec^2 p dp)/(sec^4 p)) = ∫ tan^2 p cos^2 p dp = ∫ ((1/2)−(1/2)cos 2p) dp = (1/2)p −(1/4)sin 2p =(1/2)tan^(−1) (x)−(x/(2(x^2 +1))) I= 2−(1/2)(tan^(−1) ((√2)+1)−tan^(−1) ((√2)−1)) −(1/2)((((√2)+1)/(4+2(√2))) −(((√2)−1)/(4−2(√2))))](Q101602.png)
| ||
Question and Answers Forum | ||
Question Number 101601 by Dwaipayan Shikari last updated on 03/Jul/20 | ||
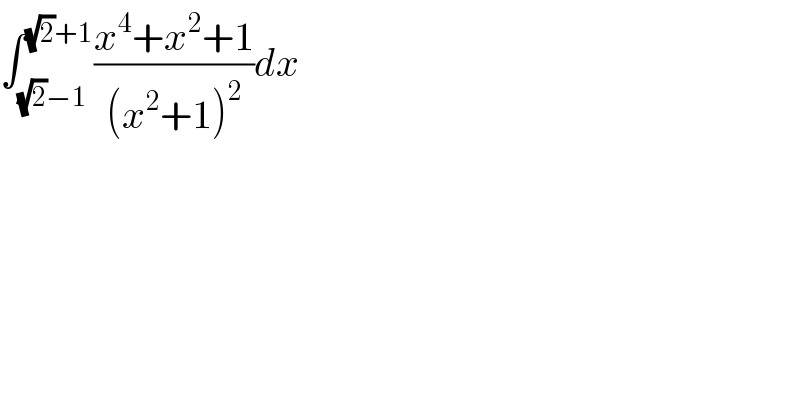 | ||
Answered by bemath last updated on 03/Jul/20 | ||
![∫ (((x^2 +1)^2 −x^2 )/((x^2 +1)^2 )) dx = x−∫ (x^2 /((x^2 +1)^2 )) dx I_2 = ∫ (x^2 /((x^2 +1)^2 )) dx [ x = tan p ] I_2 = ∫ ((tan^2 p . sec^2 p dp)/(sec^4 p)) = ∫ tan^2 p cos^2 p dp = ∫ ((1/2)−(1/2)cos 2p) dp = (1/2)p −(1/4)sin 2p =(1/2)tan^(−1) (x)−(x/(2(x^2 +1))) I= 2−(1/2)(tan^(−1) ((√2)+1)−tan^(−1) ((√2)−1)) −(1/2)((((√2)+1)/(4+2(√2))) −(((√2)−1)/(4−2(√2))))](Q101602.png) | ||
| ||