
Question and Answers Forum
Question Number 2004 by Yozzi last updated on 29/Oct/15
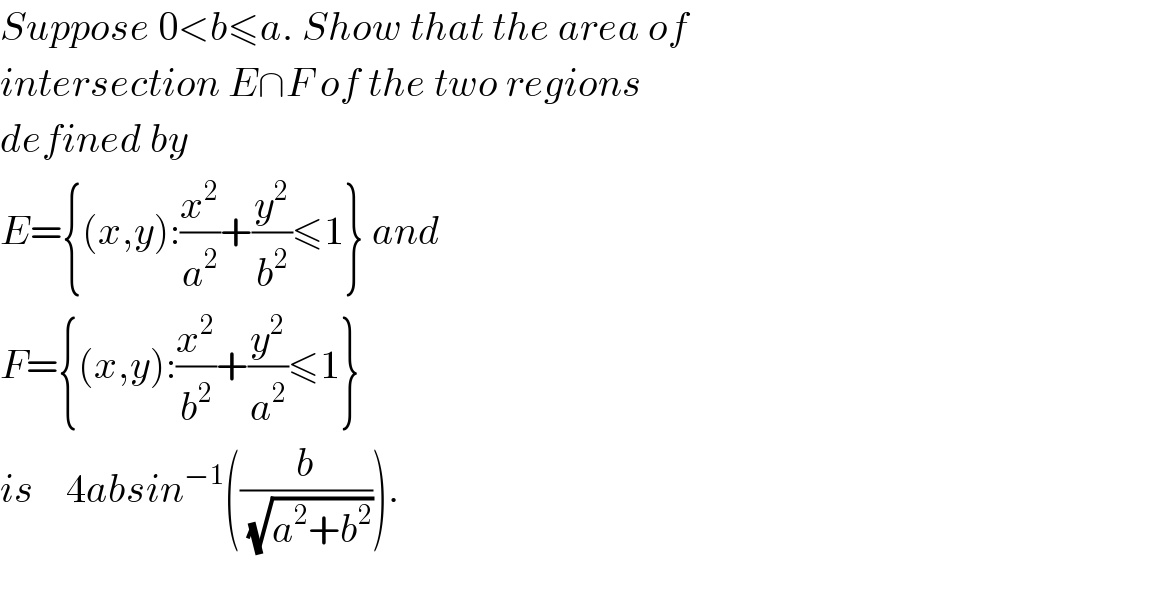
Answered by Rasheed Soomro last updated on 08/Nov/15
![Strategy • E^(⌢) :(x^2 /a^2 )+(y^2 /b^2 )=1 (1) and F^(⌢) :(x^2 /b^2 )+(y^2 /a^2 )=1 (2) are equations of ellipses which are boundary−curves of the regions E and F respectively. •For E∩F≠φ the two ellipses intersect at two points.Let these points are A(x_1 ,y_1 ) and B(x_2 ,y_2 ). •AB^(−) (common chord) divides each of the E and F regions into two parts(segments). • Let e and f are the areas of respective segments of E and F which make E∩F and A =E∩F. Then A=e+f •Let the coordinate system is so changed that A(x_1 ,y_1 ) is origin and x−axis is passed through B in new coordinate system. The coordinates of A and B will be: A=(0,0) and B=(mAB^(−) ,0) mAB^(−) =(√((x_2 −x_1 )^2 +(y_2 −y_1 )^2 )) • e is the area between curve and x−axis from x=0 to x=mAB^(−) . So as f. Hence e and f can be determined using definite_(−) integral_(−) of the curve. ∗∗∗∗∗ Determine intersection points A(x_1 ,y_1 ) and B(x_2 ,y_2 ) ⇒y=±((ab)/(√(a^2 +b^2 ))) ⇒x=±((ab)/(√(a^2 +b^2 ))) {(((ab)/(√(a^2 +b^2 ))),((ab)/(√(a^2 +b^2 )))),(((ab)/(√(a^2 +b^2 ))),((−ab)/(√(a^2 +b^2 )))), ( ((−ab)/(√(a^2 +b^2 ))),((ab)/(√(a^2 +b^2 )))),(((−ab)/(√(a^2 +b^2 ))),((−ab)/(√(a^2 +b^2 ))))} −−−−−−−− mAB^(−) =((2ab)/(√(a^2 +b^2 ))) , ((2(√(2 ))ab)/(√(a^2 +b^2 ))) −−−−−−−− e=∫_0 ^(mAB^(−) ) (±b(√(1−(x^2 /a^2 ))) )dx=±(b/a)∫_0 ^(mAB^(−) ) (√(a^2 −x^2 )) dx =±(b/a)∣(x/2)(√(a^2 −x^2 ))+(a^2 /2)sin^(−1) (x/a) +C∣_0 ^(mAB^(−) ) =±(b/a){[((((2ab)/(√(a^2 +b^2 ))) )/2)(√(a^2 −(((2ab)/(√(a^2 +b^2 ))))^2 ))+(a^2 /2)sin^(−1) (((((2ab)/(√(a^2 +b^2 )))))/a) +C] −[(0/2)(√(a^2 −(0)^2 ))+(a^2 /2)sin^(−1) (0/a) +C]} f=∫_0 ^(mAB^(−) ) (±a(√(1−(x^2 /b^2 ))) )dx=±(a/b)∫_0 ^(mAB^(−) ) (√(b^2 −x^2 )) dx Continue](Q2162.png)
| ||
Question and Answers Forum | ||
Question Number 2004 by Yozzi last updated on 29/Oct/15 | ||
 | ||
Answered by Rasheed Soomro last updated on 08/Nov/15 | ||
![Strategy • E^(⌢) :(x^2 /a^2 )+(y^2 /b^2 )=1 (1) and F^(⌢) :(x^2 /b^2 )+(y^2 /a^2 )=1 (2) are equations of ellipses which are boundary−curves of the regions E and F respectively. •For E∩F≠φ the two ellipses intersect at two points.Let these points are A(x_1 ,y_1 ) and B(x_2 ,y_2 ). •AB^(−) (common chord) divides each of the E and F regions into two parts(segments). • Let e and f are the areas of respective segments of E and F which make E∩F and A =E∩F. Then A=e+f •Let the coordinate system is so changed that A(x_1 ,y_1 ) is origin and x−axis is passed through B in new coordinate system. The coordinates of A and B will be: A=(0,0) and B=(mAB^(−) ,0) mAB^(−) =(√((x_2 −x_1 )^2 +(y_2 −y_1 )^2 )) • e is the area between curve and x−axis from x=0 to x=mAB^(−) . So as f. Hence e and f can be determined using definite_(−) integral_(−) of the curve. ∗∗∗∗∗ Determine intersection points A(x_1 ,y_1 ) and B(x_2 ,y_2 ) ⇒y=±((ab)/(√(a^2 +b^2 ))) ⇒x=±((ab)/(√(a^2 +b^2 ))) {(((ab)/(√(a^2 +b^2 ))),((ab)/(√(a^2 +b^2 )))),(((ab)/(√(a^2 +b^2 ))),((−ab)/(√(a^2 +b^2 )))), ( ((−ab)/(√(a^2 +b^2 ))),((ab)/(√(a^2 +b^2 )))),(((−ab)/(√(a^2 +b^2 ))),((−ab)/(√(a^2 +b^2 ))))} −−−−−−−− mAB^(−) =((2ab)/(√(a^2 +b^2 ))) , ((2(√(2 ))ab)/(√(a^2 +b^2 ))) −−−−−−−− e=∫_0 ^(mAB^(−) ) (±b(√(1−(x^2 /a^2 ))) )dx=±(b/a)∫_0 ^(mAB^(−) ) (√(a^2 −x^2 )) dx =±(b/a)∣(x/2)(√(a^2 −x^2 ))+(a^2 /2)sin^(−1) (x/a) +C∣_0 ^(mAB^(−) ) =±(b/a){[((((2ab)/(√(a^2 +b^2 ))) )/2)(√(a^2 −(((2ab)/(√(a^2 +b^2 ))))^2 ))+(a^2 /2)sin^(−1) (((((2ab)/(√(a^2 +b^2 )))))/a) +C] −[(0/2)(√(a^2 −(0)^2 ))+(a^2 /2)sin^(−1) (0/a) +C]} f=∫_0 ^(mAB^(−) ) (±a(√(1−(x^2 /b^2 ))) )dx=±(a/b)∫_0 ^(mAB^(−) ) (√(b^2 −x^2 )) dx Continue](Q2162.png) | ||
| ||