
Question and Answers Forum
Question Number 20091 by Tinkutara last updated on 21/Aug/17
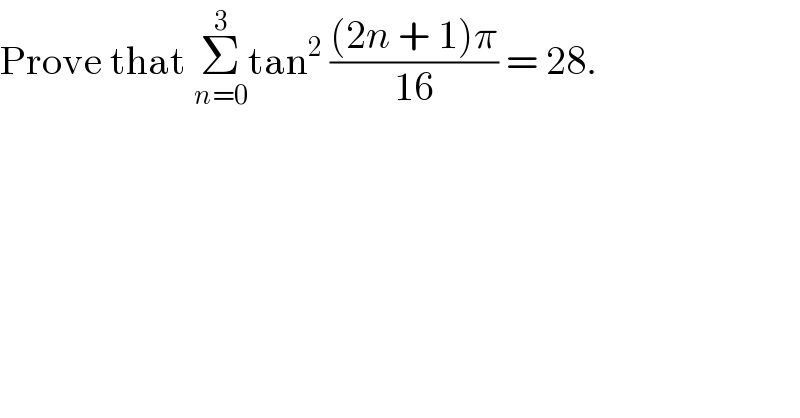
Answered by ajfour last updated on 21/Aug/17
![((sin^2 A)/(cos^2 A))+((sin^2 B)/(cos^2 B))=((sin^2 Acos^2 B+cos^2 Asin^2 B)/(cos^2 Acos^2 B)) =(([sin (A+B)+sin (A−B)]^2 +[sin (A+B)−sin (A−B)]^2 )/([cos (A+B)+cos (A−B)]^2 )) =((2[sin^2 (A+B)+sin^2 (A−B)])/([cos (A+B)+cos (A−B)]^2 )) For A=(π/(16)) , B=((7π)/(16)) ; C=((3π)/(16)) , D=((5π)/(16)) sin (A+B)= sin (C+D)=1 ; cos (A+B)= cos (C+D)= 0 , hence Σtan^2 (((2n+1)π)/(16)) = ((2[1+sin^2 ((3π)/8)])/(cos^2 ((3π)/8))) + ((2[1+sin^2 (π/8)])/(cos^2 (π/8))) = ((4+4sin^2 ((3π)/8))/(2cos^2 ((3π)/8))) + ((4+4sin^2 (π/8))/(2cos^2 (π/8))) =((4+2−2cos ((3π)/4))/(1+cos ((3π)/4))) + ((4+2−2cos (π/4))/(1+cos (π/4))) =((6+(√2))/((1−(1/(√2))))) + ((6−(√2))/((1+(1/(√2))))) =((6(√2)+2)/((√2)−1))+((6(√2)−2)/((√2)+1)) =(12+6(√2)+2(√2)+2)+(12−6(√2)−2(√2)+2) = 28 .](Q20096.png)
Commented by Tinkutara last updated on 21/Aug/17
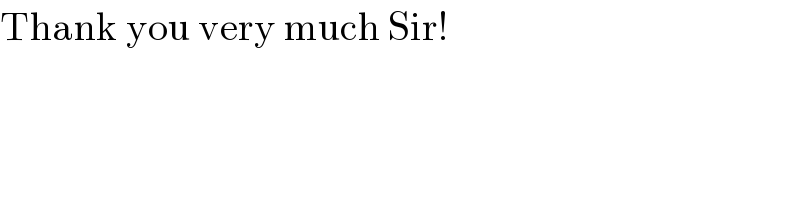
| ||
Question and Answers Forum | ||
Question Number 20091 by Tinkutara last updated on 21/Aug/17 | ||
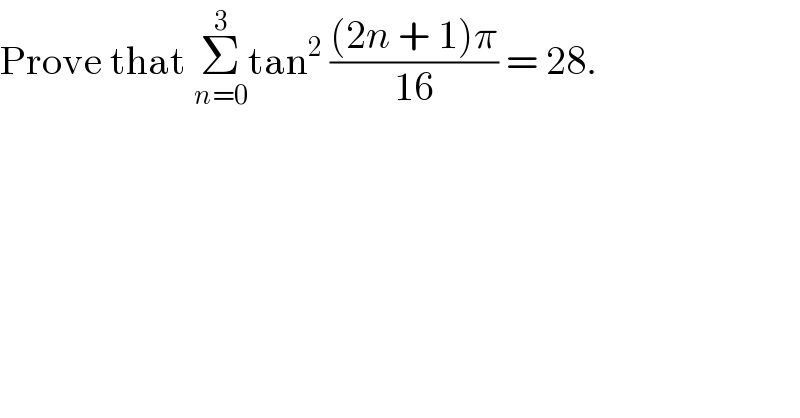 | ||
Answered by ajfour last updated on 21/Aug/17 | ||
![((sin^2 A)/(cos^2 A))+((sin^2 B)/(cos^2 B))=((sin^2 Acos^2 B+cos^2 Asin^2 B)/(cos^2 Acos^2 B)) =(([sin (A+B)+sin (A−B)]^2 +[sin (A+B)−sin (A−B)]^2 )/([cos (A+B)+cos (A−B)]^2 )) =((2[sin^2 (A+B)+sin^2 (A−B)])/([cos (A+B)+cos (A−B)]^2 )) For A=(π/(16)) , B=((7π)/(16)) ; C=((3π)/(16)) , D=((5π)/(16)) sin (A+B)= sin (C+D)=1 ; cos (A+B)= cos (C+D)= 0 , hence Σtan^2 (((2n+1)π)/(16)) = ((2[1+sin^2 ((3π)/8)])/(cos^2 ((3π)/8))) + ((2[1+sin^2 (π/8)])/(cos^2 (π/8))) = ((4+4sin^2 ((3π)/8))/(2cos^2 ((3π)/8))) + ((4+4sin^2 (π/8))/(2cos^2 (π/8))) =((4+2−2cos ((3π)/4))/(1+cos ((3π)/4))) + ((4+2−2cos (π/4))/(1+cos (π/4))) =((6+(√2))/((1−(1/(√2))))) + ((6−(√2))/((1+(1/(√2))))) =((6(√2)+2)/((√2)−1))+((6(√2)−2)/((√2)+1)) =(12+6(√2)+2(√2)+2)+(12−6(√2)−2(√2)+2) = 28 .](Q20096.png) | ||
| ||
Commented by Tinkutara last updated on 21/Aug/17 | ||
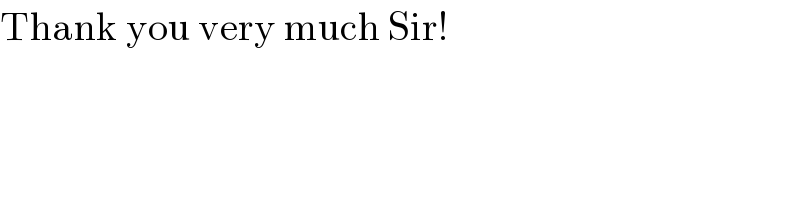 | ||