
Question and Answers Forum
Question Number 20157 by ajfour last updated on 23/Aug/17

Commented by ajfour last updated on 23/Aug/17
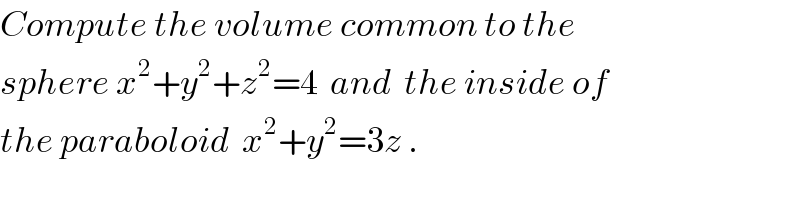
Answered by ajfour last updated on 23/Aug/17

Commented by ajfour last updated on 23/Aug/17
![Let x^2 +y^2 =r^2 ⇒ equation of sphere becomes r^2 +z^2 =4 equation of paraboloid is r^2 =3z intersection is a circle of radius r_0 . r_0 ^2 +z_0 ^2 =4 & r_0 ^2 =3z_0 ⇒ z_0 ^2 +3z_0 =4 ⇒ z_0 =1 , r_0 =(√3) . If enclosed volume is V, V=∫_0 ^( r_0 ) (2πr)dr(Δz) =2π∫_0 ^( (√3)) ((√(4−r^2 ))−(r^2 /3))rdr =2π[−(1/3)(4−r^2 )^(3/2) −(r^4 /(12))]∣_0 ^(√3) =2π[−(1/3)+(8/3)−(3/4)] =2π(((28−9)/(12))) V =((19π)/6) .](Q20178.png)
| ||
Question and Answers Forum | ||
Question Number 20157 by ajfour last updated on 23/Aug/17 | ||
 | ||
Commented by ajfour last updated on 23/Aug/17 | ||
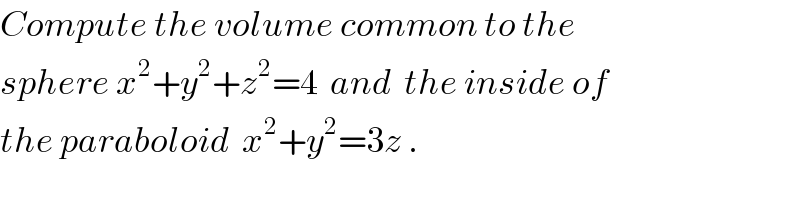 | ||
Answered by ajfour last updated on 23/Aug/17 | ||
 | ||
Commented by ajfour last updated on 23/Aug/17 | ||
![Let x^2 +y^2 =r^2 ⇒ equation of sphere becomes r^2 +z^2 =4 equation of paraboloid is r^2 =3z intersection is a circle of radius r_0 . r_0 ^2 +z_0 ^2 =4 & r_0 ^2 =3z_0 ⇒ z_0 ^2 +3z_0 =4 ⇒ z_0 =1 , r_0 =(√3) . If enclosed volume is V, V=∫_0 ^( r_0 ) (2πr)dr(Δz) =2π∫_0 ^( (√3)) ((√(4−r^2 ))−(r^2 /3))rdr =2π[−(1/3)(4−r^2 )^(3/2) −(r^4 /(12))]∣_0 ^(√3) =2π[−(1/3)+(8/3)−(3/4)] =2π(((28−9)/(12))) V =((19π)/6) .](Q20178.png) | ||