Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20297 by Tinkutara last updated on 25/Aug/17

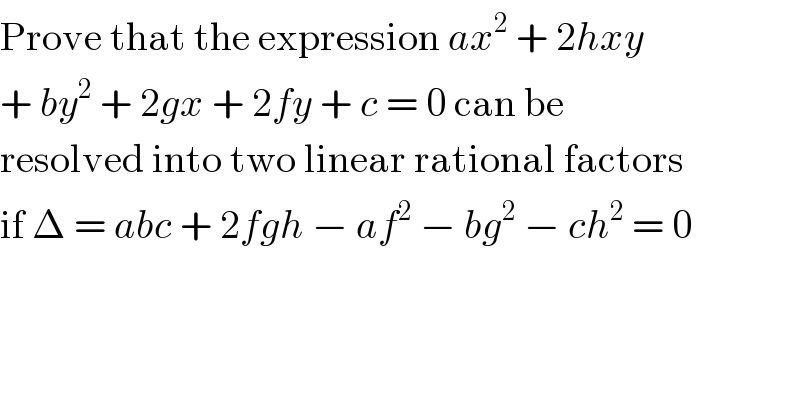
Prove that the expression ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0 can be resolved into two linear rational factors if Δ = abc + 2fgh − af^2 − bg^2 − ch^2 = 0

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{expression}\:{ax}^{\mathrm{2}} \:+\:\mathrm{2}{hxy} \\ $$$$+\:{by}^{\mathrm{2}} \:+\:\mathrm{2}{gx}\:+\:\mathrm{2}{fy}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{resolved}\:\mathrm{into}\:\mathrm{two}\:\mathrm{linear}\:\mathrm{rational}\:\mathrm{factors} \\ $$$$\mathrm{if}\:\Delta\:=\:{abc}\:+\:\mathrm{2}{fgh}\:−\:{af}^{\mathrm{2}} \:−\:{bg}^{\mathrm{2}} \:−\:{ch}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$

Answered by ajfour last updated on 25/Aug/17

let a(x−x_0 )^2 +b(y−y_0 )^2 + 2h(x−x_0 )(y−y_0 )=ax^2 +by^2 +2hxy 2gx+2fy+c=0 comparing coefficients of x and y, and constant term we get: ax_0 +hy_0 =−g .....(i) by_0 +hx_0 =−f ......(ii) ax_0 ^2 +by_0 ^2 +2hx_0 y_0 =c (iii) using (i) and (ii) in (iii): ⇒ x_0 (−g−hx_0 )+y_0 (−f−hx_0 ) +2hx_0 y_0 =c or gx_0 +fy_0 =−c ....(iv) (i) , (ii), and (iv) form a system of three linear equations in two unknowns, has unique solution only if determinant ((a,h,g),(h,b,f),(g,f,c))=0 first row we get from coefficients of x, y, and constant term of equation (i), second row→(ii) third row → (iv) ⇒a(bc−f^2 )−h(ch−gf)+g(hf−bg)=0 ⇒ abc+2fgh−af^2 −ch^2 −bg^2 =0 .

$${let}\:{a}\left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +{b}\left({y}−{y}_{\mathrm{0}} \right)^{\mathrm{2}} + \\ $$$$\:\mathrm{2}{h}\left({x}−{x}_{\mathrm{0}} \right)\left({y}−{y}_{\mathrm{0}} \right)={ax}^{\mathrm{2}} +{by}^{\mathrm{2}} +\mathrm{2}{hxy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{gx}+\mathrm{2}{fy}+{c}=\mathrm{0} \\ $$$${comparing}\:{coefficients}\:{of}\:{x}\:{and} \\ $$$${y},\:{and}\:{constant}\:{term}\:{we}\:{get}: \\ $$$$\:\:{ax}_{\mathrm{0}} +{hy}_{\mathrm{0}} =−{g}\:\:\:\:\:.....\left({i}\right) \\ $$$$\:\:{by}_{\mathrm{0}} +{hx}_{\mathrm{0}} =−{f}\:\:\:\:\:......\left({ii}\right) \\ $$$${ax}_{\mathrm{0}} ^{\mathrm{2}} +{by}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{hx}_{\mathrm{0}} {y}_{\mathrm{0}} ={c}\:\:\:\left({iii}\right) \\ $$$${using}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{in}\:\left({iii}\right): \\ $$$$\Rightarrow\:{x}_{\mathrm{0}} \left(−{g}−{hx}_{\mathrm{0}} \right)+{y}_{\mathrm{0}} \left(−{f}−{hx}_{\mathrm{0}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{hx}_{\mathrm{0}} {y}_{\mathrm{0}} ={c} \\ $$$${or}\:\:\:\:\:{gx}_{\mathrm{0}} +{fy}_{\mathrm{0}} =−{c}\:\:\:\:\:....\left({iv}\right) \\ $$$$\left({i}\right)\:,\:\left({ii}\right),\:{and}\:\left({iv}\right)\:{form}\:{a}\:{system} \\ $$$${of}\:{three}\:{linear}\:{equations}\:{in}\:{two} \\ $$$${unknowns},\:{has}\:{unique}\:{solution}\:{only}\:{if} \\ $$$$\begin{vmatrix}{{a}}&{{h}}&{{g}}\\{{h}}&{{b}}&{{f}}\\{{g}}&{{f}}&{{c}}\end{vmatrix}=\mathrm{0} \\ $$$${first}\:{row}\:{we}\:{get}\:{from}\:{coefficients} \\ $$$${of}\:{x},\:{y},\:{and}\:{constant}\:{term}\:{of} \\ $$$${equation}\:\left({i}\right),\:\:{second}\:{row}\rightarrow\left({ii}\right) \\ $$$${third}\:{row}\:\rightarrow\:\left({iv}\right) \\ $$$$\Rightarrow{a}\left({bc}−{f}^{\mathrm{2}} \right)−{h}\left({ch}−{gf}\right)+{g}\left({hf}−{bg}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{abc}+\mathrm{2}{fgh}−{af}^{\mathrm{2}} −{ch}^{\mathrm{2}} −{bg}^{\mathrm{2}} =\mathrm{0}\:. \\ $$

Commented by Tinkutara last updated on 25/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com