Question and Answers Forum
Question Number 20307 by Tinkutara last updated on 25/Aug/17
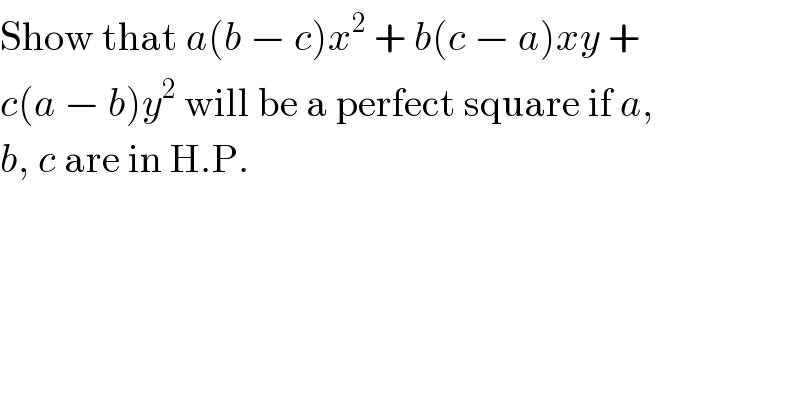
Answered by ajfour last updated on 25/Aug/17
![=x^2 [c(a−b)((y/x))^2 +b(c−a)((y/x))+a(b−c)] =c(a−b)x^2 {((y/x))^2 +2[((b(c−a))/(2c(a−b)))]x+ [((b(c−a))/(2c(a−b)))]^2 }−((b^2 (c−a)^2 )/(4c(a−b)))+a(b−c) =c(a−b)x^2 {(y/x)+((b(c−a))/(2c(a−b)))}^2 + ((4ac(a−b)(b−c)−b^2 (c−a)^2 )/(4c(a−b))) ⇒ expression is a perfect square if the constant term is zero, ⇒ 4ac(ab−ac−b^2 +bc) =b^2 c^2 −2b^2 ac+a^2 b^2 ⇒ 4a^2 bc−4a^2 c^2 −4b^2 ac+4abc^2 =b^2 c^2 −2b^2 ac+a^2 b^2 ⇒ 4abc(a+c)=4a^2 c^2 +b^2 (a^2 +c^2 +2ac) ⇒ 4abc(a+c)=4a^2 c^2 +b^2 (a+c)^2 ⇒ [b(a+c)−2ac]^2 =0 ⇒ b=((2ac)/(a+c)) ⇒ a, b, c need be in H.P. •](Q20328.png)
Commented by Tinkutara last updated on 25/Aug/17
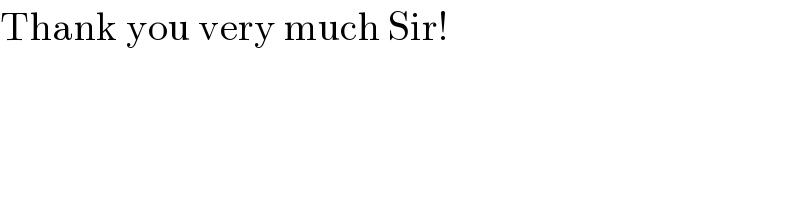
Answered by $@ty@m last updated on 26/Aug/17
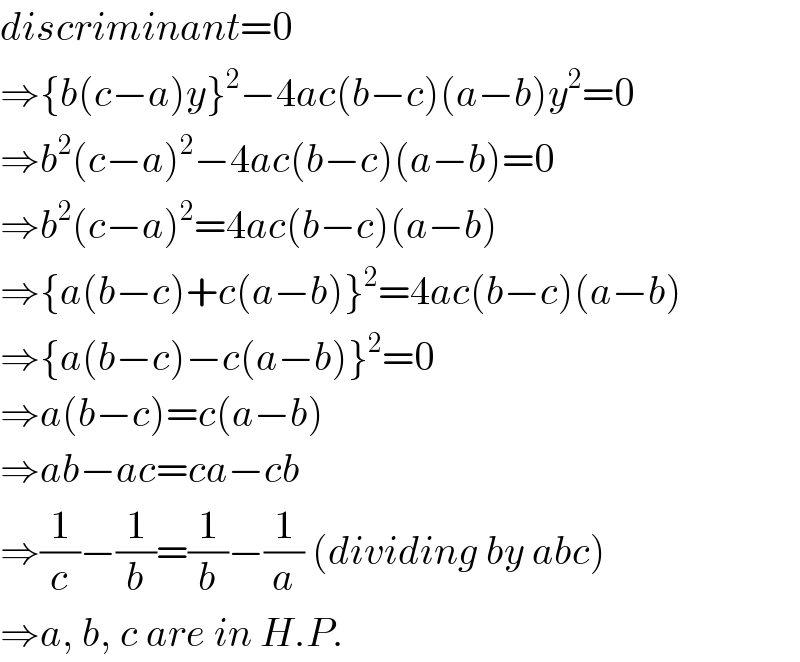
Commented by $@ty@m last updated on 25/Aug/17
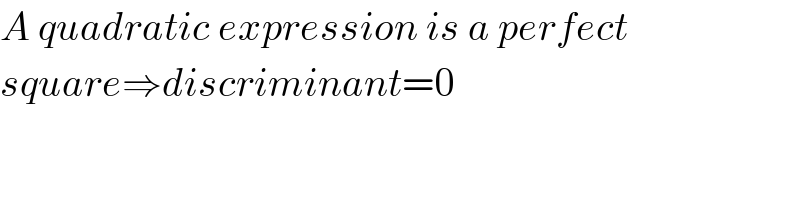
Commented by ajfour last updated on 25/Aug/17

Commented by Tinkutara last updated on 25/Aug/17

Commented by $@ty@m last updated on 26/Aug/17