Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20372 by Tinkutara last updated on 26/Aug/17

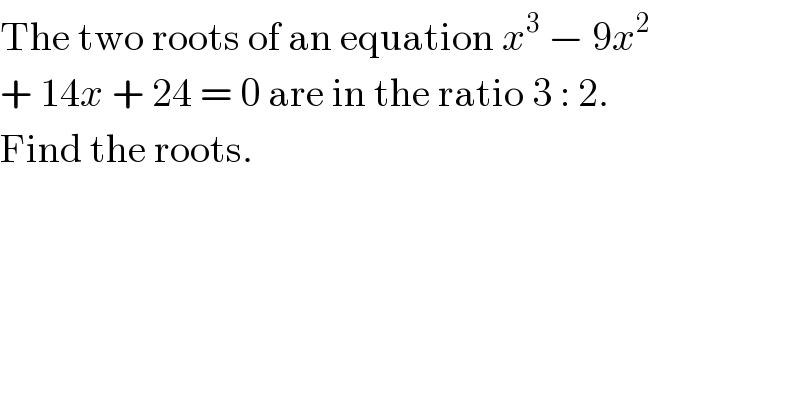
The two roots of an equation x^3 − 9x^2 + 14x + 24 = 0 are in the ratio 3 : 2. Find the roots.

$$\mathrm{The}\:\mathrm{two}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{an}\:\mathrm{equation}\:{x}^{\mathrm{3}} \:−\:\mathrm{9}{x}^{\mathrm{2}} \\ $$$$+\:\mathrm{14}{x}\:+\:\mathrm{24}\:=\:\mathrm{0}\:\mathrm{are}\:\mathrm{in}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{3}\::\:\mathrm{2}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{roots}. \\ $$

Answered by $@ty@m last updated on 26/Aug/17

α+3β+2β=9 ⇒α+5β=9−−(1) 3αβ+6β^2 +2αβ=14⇒6β^2 +5αβ=14−−(2) 6αβ^2 =−24−−(3) Eliminating α from(1) and (2), 6β^2 +5(9−5β)β=14 19β^2 −45β+14=0 β=((45±(√(2025−1064)))/(38)) β=((45±31)/(38)) β=((76)/(38)), ((14)/(38)) β=2, (7/(19)) ⇒α=−1, ((136)/(19)) the fractional values of α and β do not satisfy equation (3) ∴ α=−1, β=2 ∴ Roots of the given equation are −1,6 and 4

$$\alpha+\mathrm{3}\beta+\mathrm{2}\beta=\mathrm{9}\:\Rightarrow\alpha+\mathrm{5}\beta=\mathrm{9}−−\left(\mathrm{1}\right) \\ $$$$\mathrm{3}\alpha\beta+\mathrm{6}\beta^{\mathrm{2}} +\mathrm{2}\alpha\beta=\mathrm{14}\Rightarrow\mathrm{6}\beta^{\mathrm{2}} +\mathrm{5}\alpha\beta=\mathrm{14}−−\left(\mathrm{2}\right) \\ $$$$\mathrm{6}\alpha\beta^{\mathrm{2}} =−\mathrm{24}−−\left(\mathrm{3}\right) \\ $$$${Eliminating}\:\:\alpha\:{from}\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right), \\ $$$$\mathrm{6}\beta^{\mathrm{2}} +\mathrm{5}\left(\mathrm{9}−\mathrm{5}\beta\right)\beta=\mathrm{14} \\ $$$$\mathrm{19}\beta^{\mathrm{2}} −\mathrm{45}\beta+\mathrm{14}=\mathrm{0} \\ $$$$\beta=\frac{\mathrm{45}\pm\sqrt{\mathrm{2025}−\mathrm{1064}}}{\mathrm{38}} \\ $$$$\beta=\frac{\mathrm{45}\pm\mathrm{31}}{\mathrm{38}} \\ $$$$\beta=\frac{\mathrm{76}}{\mathrm{38}},\:\frac{\mathrm{14}}{\mathrm{38}} \\ $$$$\beta=\mathrm{2},\:\frac{\mathrm{7}}{\mathrm{19}} \\ $$$$\Rightarrow\alpha=−\mathrm{1},\:\frac{\mathrm{136}}{\mathrm{19}} \\ $$$${the}\:{fractional}\:{values}\:{of}\:\alpha\:{and} \\ $$$$\beta\:{do}\:{not}\:{satisfy}\:{equation}\:\left(\mathrm{3}\right) \\ $$$$\therefore\:\alpha=−\mathrm{1},\:\beta=\mathrm{2} \\ $$$$\therefore\:{Roots}\:{of}\:{the}\:{given}\:{equation}\:{are} \\ $$$$−\mathrm{1},\mathrm{6}\:{and}\:\mathrm{4} \\ $$

Commented by Tinkutara last updated on 26/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by ajfour last updated on 26/Aug/17

let roots be 3r,2r,γ 5r+γ=9 ; 6r^2 +5γr=14 ; 6r^2 γ=−24 ⇒ r^2 γ=−4 5r^3 +r^2 γ =9r^2 ⇒ 5r^3 −9r^2 −4=0 ...(i) from first two equations, we get ⇒ 5r^2 +(((14−6r^2 )/5))=9r 19r^2 −45r+14=0 19r^2 −38r−7r+14=0 (19r−7)(r−2)=0 r=2 satisfies (i) if r=(7/(19)), then 5((7/(19)))^3 −9((7/(19)))^2 −4=(((7)^2 )/((19)^3 ))[35−171] ≠0 . So r≠(7/(19)) r=2, α=3r=6 , β=2r=4 γ=9+5r =9−10=−1 roots are 6, 4, −1 .

$${let}\:{roots}\:{be}\:\mathrm{3}{r},\mathrm{2}{r},\gamma \\ $$$$\mathrm{5}{r}+\gamma=\mathrm{9}\:\:;\:\:\mathrm{6}{r}^{\mathrm{2}} +\mathrm{5}\gamma{r}=\mathrm{14}\:; \\ $$$$\mathrm{6}{r}^{\mathrm{2}} \gamma=−\mathrm{24}\:\Rightarrow\:\:\:{r}^{\mathrm{2}} \gamma=−\mathrm{4} \\ $$$$\:\:\:\:\mathrm{5}{r}^{\mathrm{3}} +{r}^{\mathrm{2}} \gamma\:=\mathrm{9}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{5}{r}^{\mathrm{3}} −\mathrm{9}{r}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$${from}\:{first}\:{two}\:{equations},\:{we}\:{get} \\ $$$$\Rightarrow\:\:\:\mathrm{5}{r}^{\mathrm{2}} +\left(\frac{\mathrm{14}−\mathrm{6}{r}^{\mathrm{2}} }{\mathrm{5}}\right)=\mathrm{9}{r} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{19}{r}^{\mathrm{2}} −\mathrm{45}{r}+\mathrm{14}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{19}{r}^{\mathrm{2}} −\mathrm{38}{r}−\mathrm{7}{r}+\mathrm{14}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{19}{r}−\mathrm{7}\right)\left({r}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:{r}=\mathrm{2}\:{satisfies}\:\left({i}\right) \\ $$$$\:{if}\:\:\:\:\:{r}=\frac{\mathrm{7}}{\mathrm{19}},\:{then} \\ $$$$\mathrm{5}\left(\frac{\mathrm{7}}{\mathrm{19}}\right)^{\mathrm{3}} −\mathrm{9}\left(\frac{\mathrm{7}}{\mathrm{19}}\right)^{\mathrm{2}} −\mathrm{4}=\frac{\left(\mathrm{7}\right)^{\mathrm{2}} }{\left(\mathrm{19}\right)^{\mathrm{3}} }\left[\mathrm{35}−\mathrm{171}\right] \\ $$$$\:\:\:\neq\mathrm{0}\:\:.\:{So}\:\:{r}\neq\frac{\mathrm{7}}{\mathrm{19}} \\ $$$$\:\:\:\:{r}=\mathrm{2},\:\:\:\alpha=\mathrm{3}{r}=\mathrm{6}\:,\:\beta=\mathrm{2}{r}=\mathrm{4} \\ $$$$\:\:\:\gamma=\mathrm{9}+\mathrm{5}{r}\:=\mathrm{9}−\mathrm{10}=−\mathrm{1} \\ $$$${roots}\:{are}\:\mathrm{6},\:\mathrm{4},\:−\mathrm{1}\:. \\ $$

Commented by Tinkutara last updated on 26/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Commented by $@ty@m last updated on 26/Aug/17

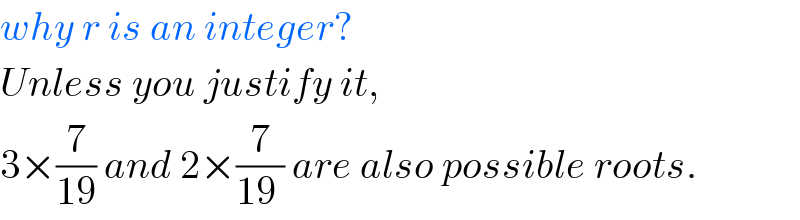
why r is an integer? Unless you justify it, 3×(7/(19)) and 2×(7/(19 )) are also possible roots.

$${why}\:{r}\:{is}\:{an}\:{integer}? \\ $$$${Unless}\:{you}\:{justify}\:{it}, \\ $$$$\mathrm{3}×\frac{\mathrm{7}}{\mathrm{19}}\:{and}\:\mathrm{2}×\frac{\mathrm{7}}{\mathrm{19}\:}\:{are}\:{also}\:{possible}\:{roots}. \\ $$

Commented by ajfour last updated on 26/Aug/17

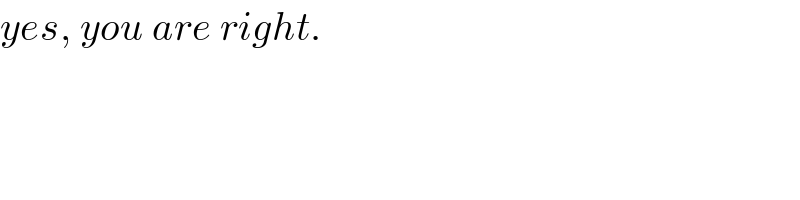
yes, you are right.

$${yes},\:{you}\:{are}\:{right}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com