
Question and Answers Forum
Question Number 20386 by tammi last updated on 26/Aug/17
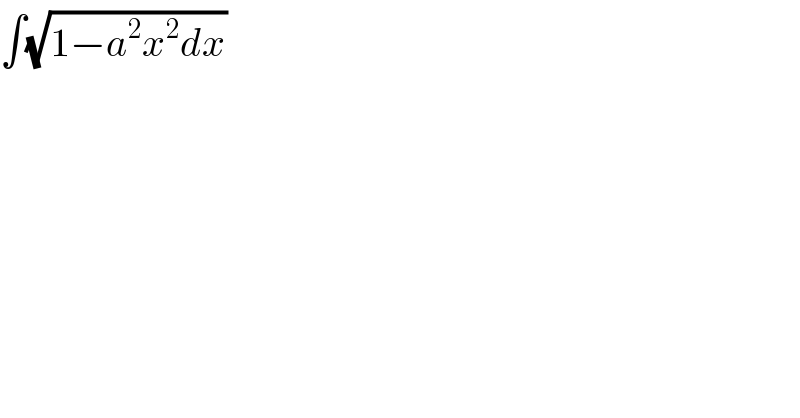
Answered by $@ty@m last updated on 26/Aug/17
![Let x=((sinθ)/a) ⇒dx=(1/a)cosθdθ ⇒I=(1/a)∫(√(1−sin^2 θ))cosθdθ =(1/a)∫cos^2 θdθ =(1/(2a))∫(1+cos2θ)dθ =(1/(2a))[θ+((sin2θ)/2)]+C =(1/(2a))[sin^(−1) ax+ax(√(1−a^2 x^2 ))]+C](Q20406.png)
| ||
Question and Answers Forum | ||
Question Number 20386 by tammi last updated on 26/Aug/17 | ||
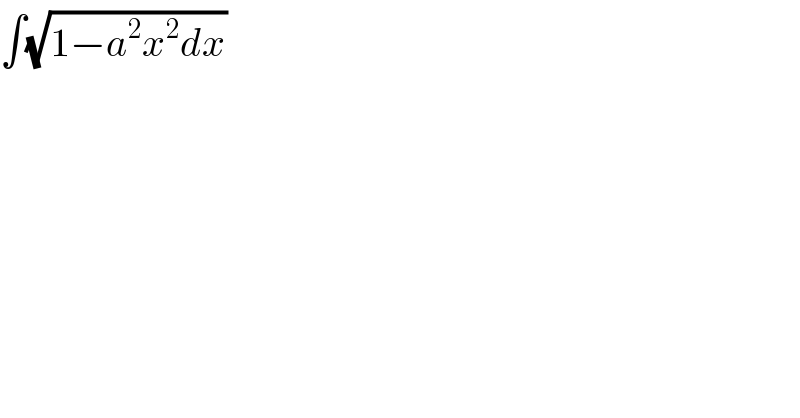 | ||
Answered by $@ty@m last updated on 26/Aug/17 | ||
![Let x=((sinθ)/a) ⇒dx=(1/a)cosθdθ ⇒I=(1/a)∫(√(1−sin^2 θ))cosθdθ =(1/a)∫cos^2 θdθ =(1/(2a))∫(1+cos2θ)dθ =(1/(2a))[θ+((sin2θ)/2)]+C =(1/(2a))[sin^(−1) ax+ax(√(1−a^2 x^2 ))]+C](Q20406.png) | ||
| ||