Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20430 by Tinkutara last updated on 26/Aug/17

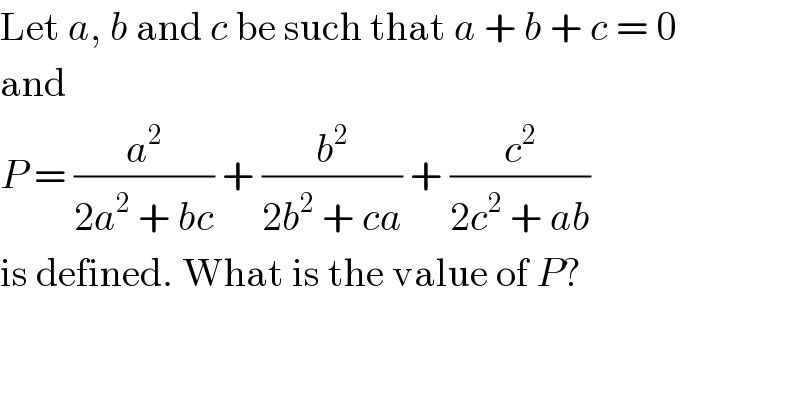
Let a, b and c be such that a + b + c = 0 and P = (a^2 /(2a^2 + bc)) + (b^2 /(2b^2 + ca)) + (c^2 /(2c^2 + ab)) is defined. What is the value of P?

$$\mathrm{Let}\:{a},\:{b}\:\mathrm{and}\:{c}\:\mathrm{be}\:\mathrm{such}\:\mathrm{that}\:{a}\:+\:{b}\:+\:{c}\:=\:\mathrm{0} \\ $$$$\mathrm{and} \\ $$$${P}\:=\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}{a}^{\mathrm{2}} \:+\:{bc}}\:+\:\frac{{b}^{\mathrm{2}} }{\mathrm{2}{b}^{\mathrm{2}} \:+\:{ca}}\:+\:\frac{{c}^{\mathrm{2}} }{\mathrm{2}{c}^{\mathrm{2}} \:+\:{ab}} \\ $$$$\mathrm{is}\:\mathrm{defined}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{P}? \\ $$

Commented by dioph last updated on 27/Aug/17

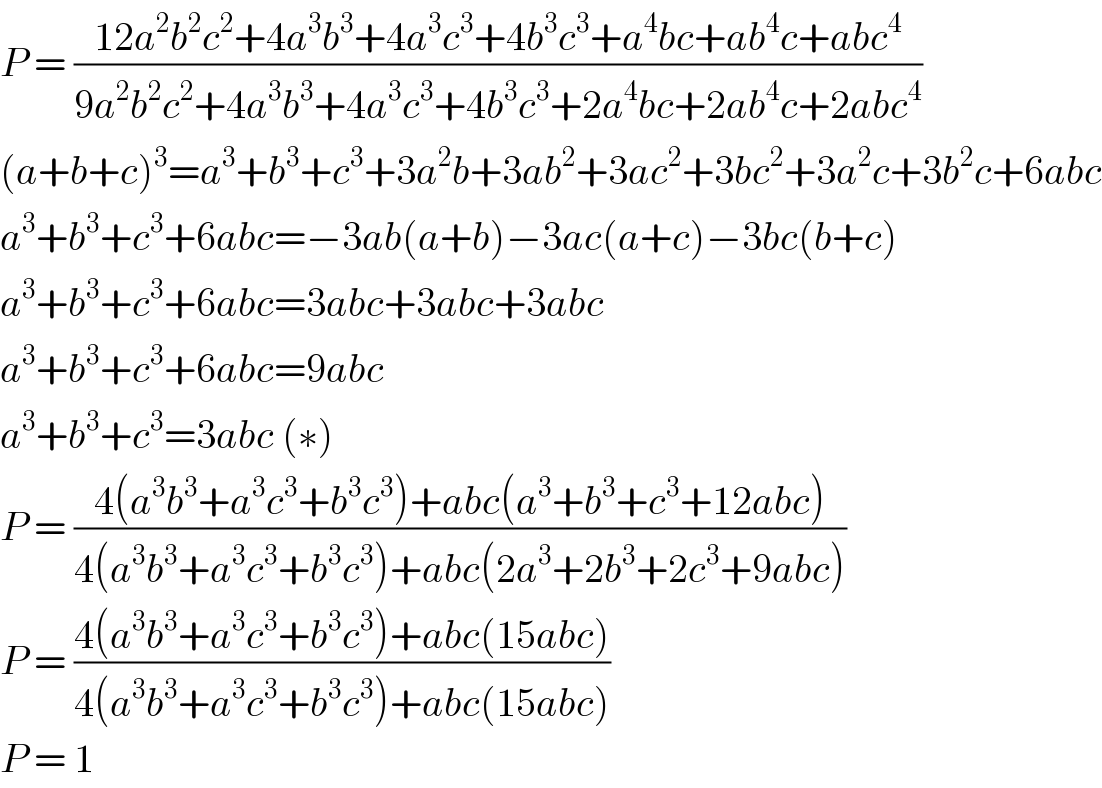
P = ((12a^2 b^2 c^2 +4a^3 b^3 +4a^3 c^3 +4b^3 c^3 +a^4 bc+ab^4 c+abc^4 )/(9a^2 b^2 c^2 +4a^3 b^3 +4a^3 c^3 +4b^3 c^3 +2a^4 bc+2ab^4 c+2abc^4 )) (a+b+c)^3 =a^3 +b^3 +c^3 +3a^2 b+3ab^2 +3ac^2 +3bc^2 +3a^2 c+3b^2 c+6abc a^3 +b^3 +c^3 +6abc=−3ab(a+b)−3ac(a+c)−3bc(b+c) a^3 +b^3 +c^3 +6abc=3abc+3abc+3abc a^3 +b^3 +c^3 +6abc=9abc a^3 +b^3 +c^3 =3abc (∗) P = ((4(a^3 b^3 +a^3 c^3 +b^3 c^3 )+abc(a^3 +b^3 +c^3 +12abc))/(4(a^3 b^3 +a^3 c^3 +b^3 c^3 )+abc(2a^3 +2b^3 +2c^3 +9abc))) P = ((4(a^3 b^3 +a^3 c^3 +b^3 c^3 )+abc(15abc))/(4(a^3 b^3 +a^3 c^3 +b^3 c^3 )+abc(15abc))) P = 1

$${P}\:=\:\frac{\mathrm{12}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{3}} {c}^{\mathrm{3}} +\mathrm{4}{b}^{\mathrm{3}} {c}^{\mathrm{3}} +{a}^{\mathrm{4}} {bc}+{ab}^{\mathrm{4}} {c}+{abc}^{\mathrm{4}} }{\mathrm{9}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{3}} {c}^{\mathrm{3}} +\mathrm{4}{b}^{\mathrm{3}} {c}^{\mathrm{3}} +\mathrm{2}{a}^{\mathrm{4}} {bc}+\mathrm{2}{ab}^{\mathrm{4}} {c}+\mathrm{2}{abc}^{\mathrm{4}} } \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{3}{ab}^{\mathrm{2}} +\mathrm{3}{ac}^{\mathrm{2}} +\mathrm{3}{bc}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} {c}+\mathrm{3}{b}^{\mathrm{2}} {c}+\mathrm{6}{abc} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{6}{abc}=−\mathrm{3}{ab}\left({a}+{b}\right)−\mathrm{3}{ac}\left({a}+{c}\right)−\mathrm{3}{bc}\left({b}+{c}\right) \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{6}{abc}=\mathrm{3}{abc}+\mathrm{3}{abc}+\mathrm{3}{abc} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{6}{abc}=\mathrm{9}{abc} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc}\:\left(\ast\right) \\ $$$${P}\:=\:\frac{\mathrm{4}\left({a}^{\mathrm{3}} {b}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} \right)+{abc}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{12}{abc}\right)}{\mathrm{4}\left({a}^{\mathrm{3}} {b}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} \right)+{abc}\left(\mathrm{2}{a}^{\mathrm{3}} +\mathrm{2}{b}^{\mathrm{3}} +\mathrm{2}{c}^{\mathrm{3}} +\mathrm{9}{abc}\right)} \\ $$$${P}\:=\:\frac{\mathrm{4}\left({a}^{\mathrm{3}} {b}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} \right)+{abc}\left(\mathrm{15}{abc}\right)}{\mathrm{4}\left({a}^{\mathrm{3}} {b}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} \right)+{abc}\left(\mathrm{15}{abc}\right)} \\ $$$${P}\:=\:\mathrm{1} \\ $$

Answered by Tinkutara last updated on 27/Aug/17

Since a + b + c = 0, ∴ a = − b − c ⇒ a^2 = − ab − ac 2a^2 + bc = a^2 − ab − ac + bc = (a − b)(a − c) Similarly, 2b^2 + ca = (b − a)(b − c), 2c^2 + ab = (c − a)(c − b) Hence, P = ((−a^2 )/((a − b)(c − a))) + ((−b^2 )/((a − b)(b − c))) + ((−c^2 )/((c − a)(b − c))) = ((−Σ_(cyc) a^2 (b − c))/((a − b)(b − c)(c − a))) After expanding the denominator, we will find this value just the same as numerator. So, P = 1.

$$\mathrm{Since}\:{a}\:+\:{b}\:+\:{c}\:=\:\mathrm{0}, \\ $$$$\therefore\:{a}\:=\:−\:{b}\:−\:{c}\:\Rightarrow\:{a}^{\mathrm{2}} \:=\:−\:{ab}\:−\:{ac} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} \:+\:{bc}\:=\:{a}^{\mathrm{2}} \:−\:{ab}\:−\:{ac}\:+\:{bc}\:=\:\left({a}\:−\:{b}\right)\left({a}\:−\:{c}\right) \\ $$$$\mathrm{Similarly},\:\mathrm{2}{b}^{\mathrm{2}} \:+\:{ca}\:=\:\left({b}\:−\:{a}\right)\left({b}\:−\:{c}\right), \\ $$$$\mathrm{2}{c}^{\mathrm{2}} \:+\:{ab}\:=\:\left({c}\:−\:{a}\right)\left({c}\:−\:{b}\right) \\ $$$$\mathrm{Hence}, \\ $$$${P}\:=\:\frac{−{a}^{\mathrm{2}} }{\left({a}\:−\:{b}\right)\left({c}\:−\:{a}\right)}\:+\:\frac{−{b}^{\mathrm{2}} }{\left({a}\:−\:{b}\right)\left({b}\:−\:{c}\right)}\:+\:\frac{−{c}^{\mathrm{2}} }{\left({c}\:−\:{a}\right)\left({b}\:−\:{c}\right)} \\ $$$$=\:\frac{−\underset{{cyc}} {\sum}{a}^{\mathrm{2}} \left({b}\:−\:{c}\right)}{\left({a}\:−\:{b}\right)\left({b}\:−\:{c}\right)\left({c}\:−\:{a}\right)} \\ $$$$\mathrm{After}\:\mathrm{expanding}\:\mathrm{the}\:\mathrm{denominator},\:\mathrm{we}\:\mathrm{will}\:\mathrm{find}\:\mathrm{this} \\ $$$$\mathrm{value}\:\mathrm{just}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{numerator}. \\ $$$$\mathrm{So},\:{P}\:=\:\mathrm{1}. \\ $$

Answered by ajfour last updated on 27/Aug/17

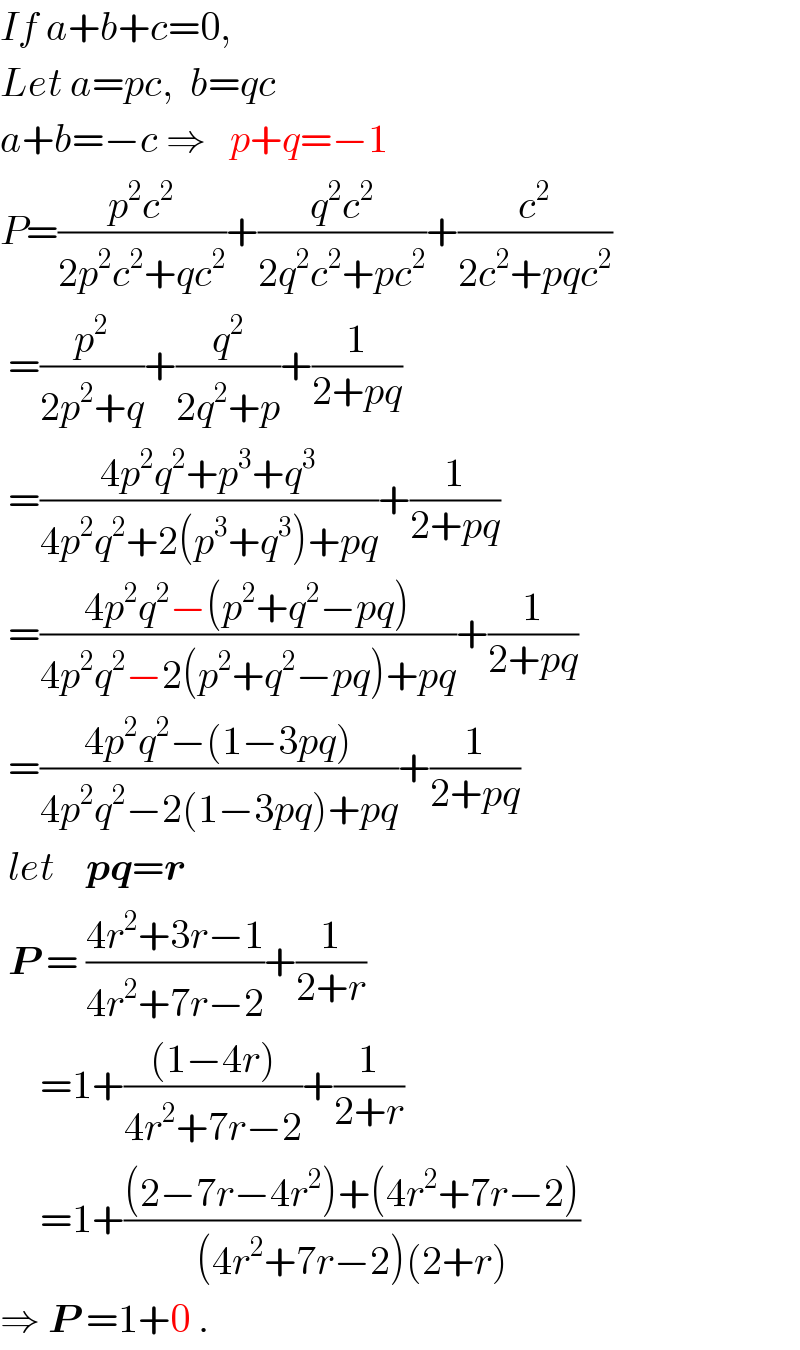
If a+b+c=0, Let a=pc, b=qc a+b=−c ⇒ p+q=−1 P=((p^2 c^2 )/(2p^2 c^2 +qc^2 ))+((q^2 c^2 )/(2q^2 c^2 +pc^2 ))+(c^2 /(2c^2 +pqc^2 )) =(p^2 /(2p^2 +q))+(q^2 /(2q^2 +p))+(1/(2+pq)) =((4p^2 q^2 +p^3 +q^3 )/(4p^2 q^2 +2(p^3 +q^3 )+pq))+(1/(2+pq)) =((4p^2 q^2 −(p^2 +q^2 −pq))/(4p^2 q^2 −2(p^2 +q^2 −pq)+pq))+(1/(2+pq)) =((4p^2 q^2 −(1−3pq))/(4p^2 q^2 −2(1−3pq)+pq))+(1/(2+pq)) let pq=r P = ((4r^2 +3r−1)/(4r^2 +7r−2))+(1/(2+r)) =1+(((1−4r))/(4r^2 +7r−2))+(1/(2+r)) =1+(((2−7r−4r^2 )+(4r^2 +7r−2))/((4r^2 +7r−2)(2+r))) ⇒ P =1+0 .

$${If}\:{a}+{b}+{c}=\mathrm{0}, \\ $$$${Let}\:{a}={pc},\:\:{b}={qc}\: \\ $$$${a}+{b}=−{c}\:\Rightarrow\:\:\:{p}+{q}=−\mathrm{1} \\ $$$${P}=\frac{{p}^{\mathrm{2}} {c}^{\mathrm{2}} }{\mathrm{2}{p}^{\mathrm{2}} {c}^{\mathrm{2}} +{qc}^{\mathrm{2}} }+\frac{{q}^{\mathrm{2}} {c}^{\mathrm{2}} }{\mathrm{2}{q}^{\mathrm{2}} {c}^{\mathrm{2}} +{pc}^{\mathrm{2}} }+\frac{{c}^{\mathrm{2}} }{\mathrm{2}{c}^{\mathrm{2}} +{pqc}^{\mathrm{2}} } \\ $$$$\:=\frac{{p}^{\mathrm{2}} }{\mathrm{2}{p}^{\mathrm{2}} +{q}}+\frac{{q}^{\mathrm{2}} }{\mathrm{2}{q}^{\mathrm{2}} +{p}}+\frac{\mathrm{1}}{\mathrm{2}+{pq}} \\ $$$$\:=\frac{\mathrm{4}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{3}} +{q}^{\mathrm{3}} }{\mathrm{4}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{2}\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)+{pq}}+\frac{\mathrm{1}}{\mathrm{2}+{pq}} \\ $$$$\:=\frac{\mathrm{4}{p}^{\mathrm{2}} {q}^{\mathrm{2}} −\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}\right)}{\mathrm{4}{p}^{\mathrm{2}} {q}^{\mathrm{2}} −\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}\right)+{pq}}+\frac{\mathrm{1}}{\mathrm{2}+{pq}} \\ $$$$\:=\frac{\mathrm{4}{p}^{\mathrm{2}} {q}^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{3}{pq}\right)}{\mathrm{4}{p}^{\mathrm{2}} {q}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\mathrm{3}{pq}\right)+{pq}}+\frac{\mathrm{1}}{\mathrm{2}+{pq}} \\ $$$$\:{let}\:\:\:\:\boldsymbol{{pq}}=\boldsymbol{{r}} \\ $$$$\:\boldsymbol{{P}}\:=\:\frac{\mathrm{4}{r}^{\mathrm{2}} +\mathrm{3}{r}−\mathrm{1}}{\mathrm{4}{r}^{\mathrm{2}} +\mathrm{7}{r}−\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}+{r}} \\ $$$$\:\:\:\:\:=\mathrm{1}+\frac{\left(\mathrm{1}−\mathrm{4}{r}\right)}{\mathrm{4}{r}^{\mathrm{2}} +\mathrm{7}{r}−\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}+{r}} \\ $$$$\:\:\:\:\:=\mathrm{1}+\frac{\left(\mathrm{2}−\mathrm{7}{r}−\mathrm{4}{r}^{\mathrm{2}} \right)+\left(\mathrm{4}{r}^{\mathrm{2}} +\mathrm{7}{r}−\mathrm{2}\right)}{\left(\mathrm{4}{r}^{\mathrm{2}} +\mathrm{7}{r}−\mathrm{2}\right)\left(\mathrm{2}+{r}\right)} \\ $$$$\Rightarrow\:\boldsymbol{{P}}\:=\mathrm{1}+\mathrm{0}\:. \\ $$

Commented by ajfour last updated on 27/Aug/17

good question, thanks.

$${good}\:{question},\:{thanks}. \\ $$

Commented by Tinkutara last updated on 27/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com