
Question and Answers Forum
Question Number 20434 by pp75718276@gmail.com last updated on 26/Aug/17
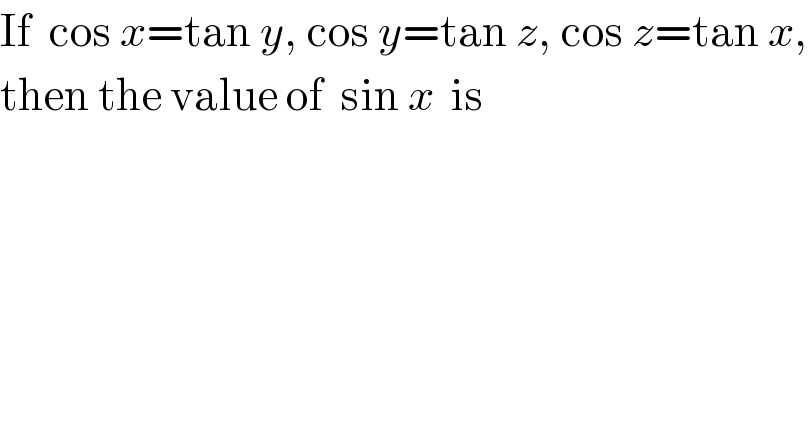
Answered by ajfour last updated on 27/Aug/17
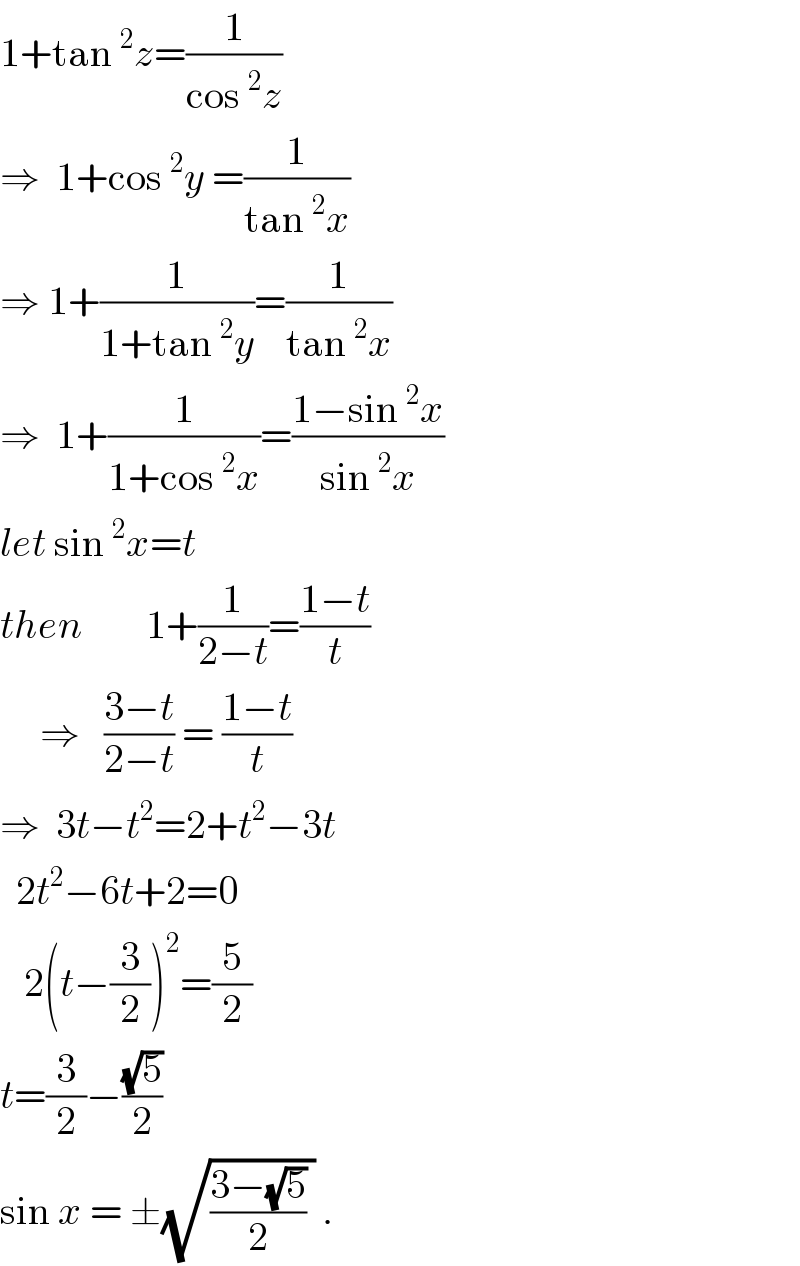
Commented by myintkhaing last updated on 27/Aug/17

Answered by Tinkutara last updated on 27/Aug/17
![cos^2 x = tan^2 y = sec^2 y − 1 = cot^2 z − 1 1+cos^2 x=cot^2 z=((cos^2 z)/(1−cos^2 z))=((tan^2 x)/(1−tan^2 x)) 2−sin^2 x=((sin^2 x)/(cos^2 x−sin^2 x))=((sin^2 x)/(1−2sin^2 x)) (2−sin^2 x)(1−2sin^2 x)=sin^2 x sin^4 x−3sin^2 x+1=0 sin^2 x=((3±(√5))/2) But sin^2 x≤1 as sin x∈[−1,1] So sin^2 x∈[0,1] sin^2 x=(1/2)(3−(√5))=(1/2)[(1/2)(1+5−2(√5))] sin^2 x=((((√5)−1)/2))^2 ⇒∣sin x∣=(((√5)−1)/2) Similarly, ∣sin y∣=∣sin z∣=(((√5)−1)/2)](Q20508.png)
| ||
Question and Answers Forum | ||
Question Number 20434 by pp75718276@gmail.com last updated on 26/Aug/17 | ||
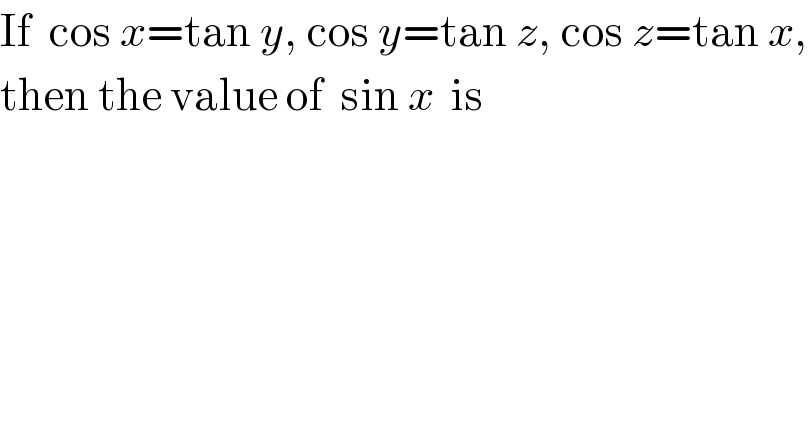 | ||
Answered by ajfour last updated on 27/Aug/17 | ||
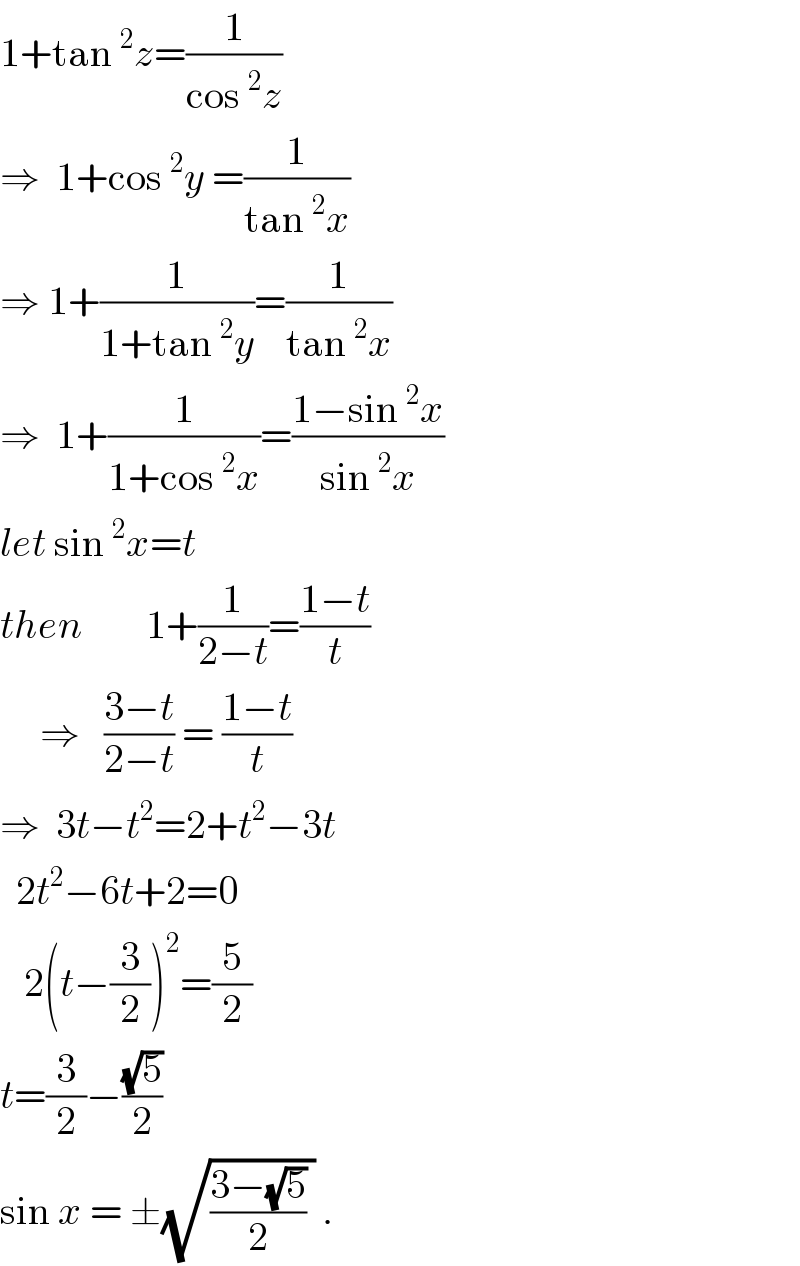 | ||
| ||
Commented by myintkhaing last updated on 27/Aug/17 | ||
 | ||
Answered by Tinkutara last updated on 27/Aug/17 | ||
![cos^2 x = tan^2 y = sec^2 y − 1 = cot^2 z − 1 1+cos^2 x=cot^2 z=((cos^2 z)/(1−cos^2 z))=((tan^2 x)/(1−tan^2 x)) 2−sin^2 x=((sin^2 x)/(cos^2 x−sin^2 x))=((sin^2 x)/(1−2sin^2 x)) (2−sin^2 x)(1−2sin^2 x)=sin^2 x sin^4 x−3sin^2 x+1=0 sin^2 x=((3±(√5))/2) But sin^2 x≤1 as sin x∈[−1,1] So sin^2 x∈[0,1] sin^2 x=(1/2)(3−(√5))=(1/2)[(1/2)(1+5−2(√5))] sin^2 x=((((√5)−1)/2))^2 ⇒∣sin x∣=(((√5)−1)/2) Similarly, ∣sin y∣=∣sin z∣=(((√5)−1)/2)](Q20508.png) | ||
| ||