Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 20471 by ajfour last updated on 27/Aug/17

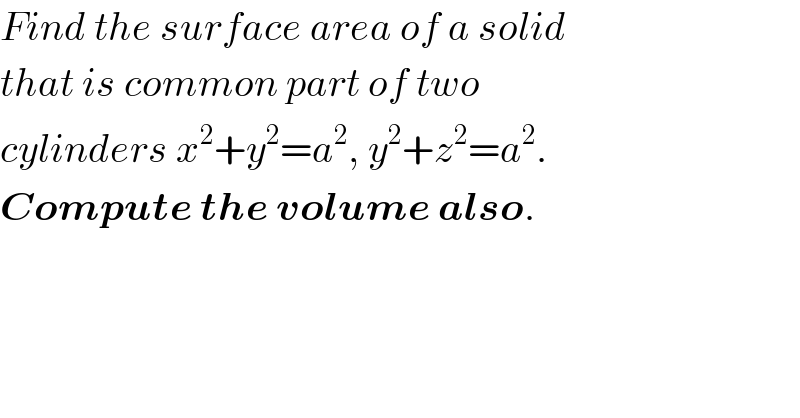
Find the surface area of a solid that is common part of two cylinders x^2 +y^2 =a^2 , y^2 +z^2 =a^2 . Compute the volume also.

$${Find}\:{the}\:{surface}\:{area}\:{of}\:{a}\:{solid} \\ $$$${that}\:{is}\:{common}\:{part}\:{of}\:{two} \\ $$$${cylinders}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} ,\:{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={a}^{\mathrm{2}} . \\ $$$$\boldsymbol{{Compute}}\:\boldsymbol{{the}}\:\boldsymbol{{volume}}\:\boldsymbol{{also}}. \\ $$

Commented by ajfour last updated on 27/Aug/17

Commented by ajfour last updated on 27/Aug/17

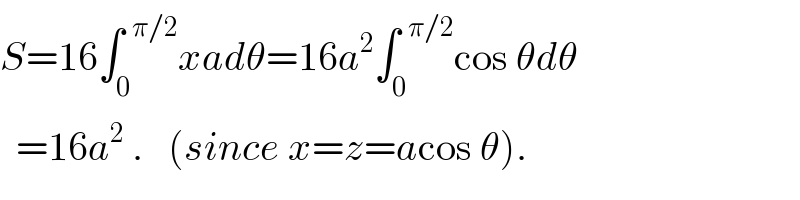
S=16∫_0 ^( π/2) xadθ=16a^2 ∫_0 ^( π/2) cos θdθ =16a^2 . (since x=z=acos θ).

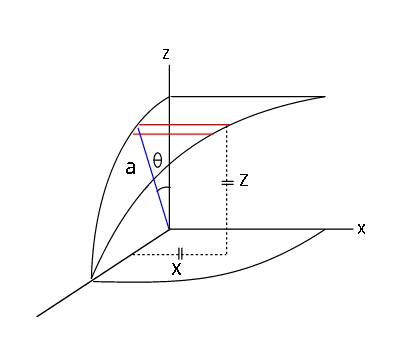
$${S}=\mathrm{16}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} {xad}\theta=\mathrm{16}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \mathrm{cos}\:\theta{d}\theta \\ $$$$\:\:=\mathrm{16}{a}^{\mathrm{2}} \:.\:\:\:\left({since}\:{x}={z}={a}\mathrm{cos}\:\theta\right). \\ $$

Answered by ajfour last updated on 28/Aug/17

V = 16∫_0 ^( a) ∫_0 ^( acos θ) (acos θ−x)dx]dy =16∫_0 ^( π/2) (axcos θ−(x^2 /2))∣_0 ^(acos θ) (acos θ)dθ =16∫_0 ^( π/2) ((a^2 cos^2 θ)/2)(acos θ)dθ =8a^3 ∫_0 ^( π/2) (1−sin^2 θ)d(sin θ) =8a^3 [sin θ−((sin^3 θ)/3)]∣_0 ^(π/2) V=((16a^3 )/3) .

$$\left.{V}\:=\:\mathrm{16}\int_{\mathrm{0}} ^{\:\:{a}} \int_{\mathrm{0}} ^{\:\:{a}\mathrm{cos}\:\theta} \left({a}\mathrm{cos}\:\theta−{x}\right){dx}\right]{dy} \\ $$$$\:=\mathrm{16}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \left({ax}\mathrm{cos}\:\theta−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{{a}\mathrm{cos}\:\theta} \left({a}\mathrm{cos}\:\theta\right){d}\theta \\ $$$$=\mathrm{16}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \:\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{2}}\left({a}\mathrm{cos}\:\theta\right){d}\theta \\ $$$$=\mathrm{8}{a}^{\mathrm{3}} \int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta\right){d}\left(\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{8}{a}^{\mathrm{3}} \left[\mathrm{sin}\:\theta−\frac{\mathrm{sin}\:^{\mathrm{3}} \theta}{\mathrm{3}}\right]\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{V}}=\frac{\mathrm{16}\boldsymbol{{a}}^{\mathrm{3}} }{\mathrm{3}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com