Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20551 by Tinkutara last updated on 28/Aug/17

Find the minimum value of ∣a + bω + cω^2 ∣, where a, b and c are all not equal integers and ω(≠1) is a cube root of unity.

$${Find}\:{the}\:{minimum}\:{value}\:{of} \\ $$$$\mid{a}\:+\:{b}\omega\:+\:{c}\omega^{\mathrm{2}} \mid,\:{where}\:{a},\:{b}\:{and}\:{c}\:{are}\:{all} \\ $$$${not}\:{equal}\:{integers}\:{and}\:\omega\left(\neq\mathrm{1}\right)\:{is}\:{a}\:{cube} \\ $$$${root}\:{of}\:{unity}. \\ $$

Commented by ajfour last updated on 28/Aug/17

Commented by ajfour last updated on 28/Aug/17

let d be the minimum magnitude. (d/(sin 60°))+2((b/2))=a ...(i) and (d/(tan 60°))+b=c ...(ii) ⇒ ((2d)/(√3))=a−b and (d/(√3))=c−b d_(min) =(√3)(c−b) = (√3) as c, b are unequal integers; their minimum difference is 1 .

$${let}\:\boldsymbol{{d}}\:{be}\:{the}\:{minimum}\:{magnitude}. \\ $$$$\frac{{d}}{\mathrm{sin}\:\mathrm{60}°}+\mathrm{2}\left(\frac{{b}}{\mathrm{2}}\right)={a}\:\:\:\:...\left({i}\right) \\ $$$${and}\:\:\frac{{d}}{\mathrm{tan}\:\mathrm{60}°}+{b}={c}\:\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow\:\:\:\:\frac{\mathrm{2}{d}}{\sqrt{\mathrm{3}}}={a}−{b}\:\:\:{and}\:\:\:\frac{{d}}{\sqrt{\mathrm{3}}}={c}−{b} \\ $$$$\:\:\boldsymbol{{d}}_{\boldsymbol{{min}}} =\sqrt{\mathrm{3}}\left(\boldsymbol{{c}}−\boldsymbol{{b}}\right)\:=\:\sqrt{\mathrm{3}} \\ $$$${as}\:{c},\:{b}\:{are}\:{unequal}\:{integers};\:{their} \\ $$$${minimum}\:{difference}\:{is}\:\mathrm{1}\:. \\ $$

Commented by Tinkutara last updated on 28/Aug/17

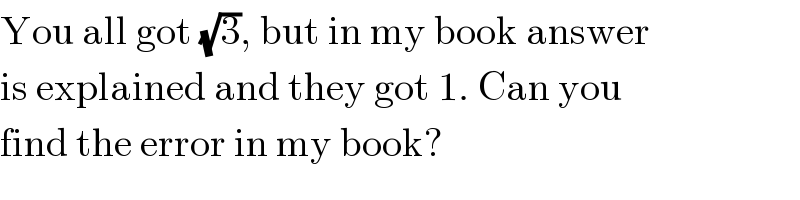
You all got (√3), but in my book answer is explained and they got 1. Can you find the error in my book?

$$\mathrm{You}\:\mathrm{all}\:\mathrm{got}\:\sqrt{\mathrm{3}},\:\mathrm{but}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book}\:\mathrm{answer} \\ $$$$\mathrm{is}\:\mathrm{explained}\:\mathrm{and}\:\mathrm{they}\:\mathrm{got}\:\mathrm{1}.\:\mathrm{Can}\:\mathrm{you} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{error}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book}? \\ $$

Commented by Tinkutara last updated on 28/Aug/17

Commented by dioph last updated on 28/Aug/17

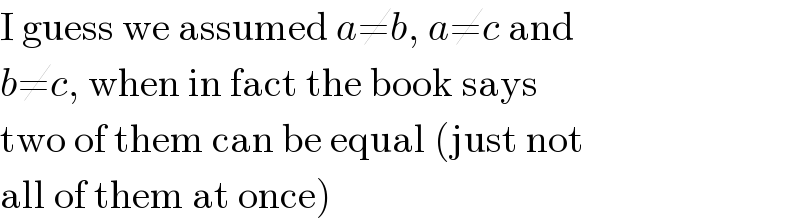
I guess we assumed a≠b, a≠c and b≠c, when in fact the book says two of them can be equal (just not all of them at once)

$$\mathrm{I}\:\mathrm{guess}\:\mathrm{we}\:\mathrm{assumed}\:{a}\neq{b},\:{a}\neq{c}\:\mathrm{and} \\ $$$${b}\neq{c},\:\mathrm{when}\:\mathrm{in}\:\mathrm{fact}\:\mathrm{the}\:\mathrm{book}\:\mathrm{says} \\ $$$$\mathrm{two}\:\mathrm{of}\:\mathrm{them}\:\mathrm{can}\:\mathrm{be}\:\mathrm{equal}\:\left(\mathrm{just}\:\mathrm{not}\right. \\ $$$$\left.\mathrm{all}\:\mathrm{of}\:\mathrm{them}\:\mathrm{at}\:\mathrm{once}\right) \\ $$

Commented by Tinkutara last updated on 28/Aug/17

So 1 is correct?

$$\mathrm{So}\:\mathrm{1}\:\mathrm{is}\:\mathrm{correct}? \\ $$

Commented by ajfour last updated on 28/Aug/17

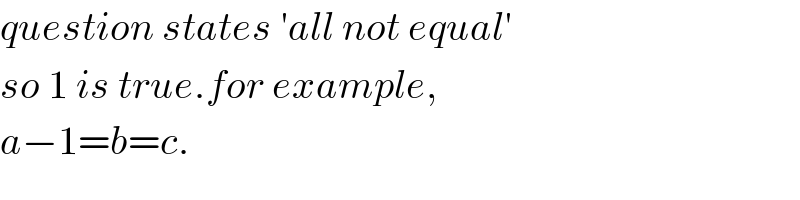
question states ′all not equal′ so 1 is true.for example, a−1=b=c.

$${question}\:{states}\:'{all}\:{not}\:{equal}' \\ $$$${so}\:\mathrm{1}\:{is}\:{true}.{for}\:{example}, \\ $$$${a}−\mathrm{1}={b}={c}. \\ $$

Commented by Tinkutara last updated on 28/Aug/17

Thank you very much ajfour Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{ajfour}\:\mathrm{Sir}! \\ $$

Answered by dioph last updated on 28/Aug/17

∣(a−(1/2)b−(1/2)c)+i(((√3)/2)b−((√3)/2)c)∣= =(√((a−(1/2)b−(1/2)c)^2 +(((√3)/2)b−((√3)/2)c)^2 ))= =(√(a^2 +(1/4)b^2 +(1/4)c^2 −ab−ac+(1/2)bc+(3/4)b^2 +(3/4)c^2 −(3/2)bc))= =(√(a^2 +b^2 +c^2 −ab−ac−bc)) min((√(a^2 +b^2 +c^2 −ab−ac−bc)))= = (√(min(a^2 +b^2 +c^2 −ab−ac−bc))) a,b,c are interchangeable, so assume a<b<c. Case 1: (a,b,c)=(b−1,b,b+1) (b−1)^2 +b^2 +(b+1)^2 −(b(b−1)+(b−1)(b+1)+b(b+1))= = b^2 −2b+1+b^2 +b^2 +2b+1−(b^2 −b+b^2 −1+b^2 +b)= = 3b^2 +2−(3b^2 −1) = 3. Case 2: (a,b,c)≠(k−1,k,k+1) Case 2.1: a < b−1 a−b−c < (b−1)−b−c a(a−b−c) > (b−1)((b−1)−b−c) a^2 −(ab+ac) > (b−1)^2 −(b−1)(b+c) a^2 +b^2 +c^2 −(ab+ac+bc) > (b−1)^2 +b^2 +c^2 −(b(b−1)+c(b−1)+bc) (a,b,c) is not optimal. Case 2.2: c > b+1 c−a−b > (b+1)−a−b c(c−a−b) > (b+1)((b+1)−a−b) c^2 −(ac+bc) > (b+1)^2 −(b+1)(a+b) a^2 +b^2 +c^2 −(ab+ac+bc) > a^2 +b^2 +(b+1)^2 −(ab+a(b+1)+b(b+1)) (a,b,c) is not optimal. Therefore, the answer is (√3).

$$\mid\left({a}−\frac{\mathrm{1}}{\mathrm{2}}{b}−\frac{\mathrm{1}}{\mathrm{2}}{c}\right)+{i}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{b}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{c}\right)\mid= \\ $$$$=\sqrt{\left({a}−\frac{\mathrm{1}}{\mathrm{2}}{b}−\frac{\mathrm{1}}{\mathrm{2}}{c}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{b}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{c}\right)^{\mathrm{2}} }= \\ $$$$=\sqrt{{a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}{b}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}{c}^{\mathrm{2}} −{ab}−{ac}+\frac{\mathrm{1}}{\mathrm{2}}{bc}+\frac{\mathrm{3}}{\mathrm{4}}{b}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{c}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}{bc}}= \\ $$$$=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{ac}−{bc}} \\ $$$$\mathrm{min}\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{ac}−{bc}}\right)= \\ $$$$=\:\sqrt{\mathrm{min}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{ac}−{bc}\right)} \\ $$$${a},{b},{c}\:\mathrm{are}\:\mathrm{interchangeable},\:\mathrm{so} \\ $$$$\mathrm{assume}\:{a}<{b}<{c}. \\ $$$$\boldsymbol{\mathrm{Case}}\:\mathrm{1}:\:\left({a},{b},{c}\right)=\left({b}−\mathrm{1},{b},{b}+\mathrm{1}\right) \\ $$$$\left({b}−\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} −\left({b}\left({b}−\mathrm{1}\right)+\left({b}−\mathrm{1}\right)\left({b}+\mathrm{1}\right)+{b}\left({b}+\mathrm{1}\right)\right)= \\ $$$$=\:{b}^{\mathrm{2}} −\mathrm{2}{b}+\mathrm{1}+{b}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}−\left({b}^{\mathrm{2}} −{b}+{b}^{\mathrm{2}} −\mathrm{1}+{b}^{\mathrm{2}} +{b}\right)= \\ $$$$=\:\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}−\left(\mathrm{3}{b}^{\mathrm{2}} −\mathrm{1}\right)\:=\:\mathrm{3}. \\ $$$$\boldsymbol{\mathrm{Case}}\:\mathrm{2}:\:\left({a},{b},{c}\right)\neq\left({k}−\mathrm{1},{k},{k}+\mathrm{1}\right) \\ $$$$\boldsymbol{\mathrm{Case}}\:\mathrm{2}.\mathrm{1}:\:{a}\:<\:{b}−\mathrm{1} \\ $$$${a}−{b}−{c}\:<\:\left({b}−\mathrm{1}\right)−{b}−{c} \\ $$$${a}\left({a}−{b}−{c}\right)\:>\:\left({b}−\mathrm{1}\right)\left(\left({b}−\mathrm{1}\right)−{b}−{c}\right) \\ $$$${a}^{\mathrm{2}} −\left({ab}+{ac}\right)\:>\:\left({b}−\mathrm{1}\right)^{\mathrm{2}} −\left({b}−\mathrm{1}\right)\left({b}+{c}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{ac}+{bc}\right)\:>\:\left({b}−\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({b}\left({b}−\mathrm{1}\right)+{c}\left({b}−\mathrm{1}\right)+{bc}\right) \\ $$$$\left({a},{b},{c}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{optimal}. \\ $$$$\boldsymbol{\mathrm{Case}}\:\mathrm{2}.\mathrm{2}:\:{c}\:>\:{b}+\mathrm{1} \\ $$$${c}−{a}−{b}\:>\:\left({b}+\mathrm{1}\right)−{a}−{b} \\ $$$${c}\left({c}−{a}−{b}\right)\:>\:\left({b}+\mathrm{1}\right)\left(\left({b}+\mathrm{1}\right)−{a}−{b}\right) \\ $$$${c}^{\mathrm{2}} −\left({ac}+{bc}\right)\:>\:\left({b}+\mathrm{1}\right)^{\mathrm{2}} −\left({b}+\mathrm{1}\right)\left({a}+{b}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{ac}+{bc}\right)\:>\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} −\left({ab}+{a}\left({b}+\mathrm{1}\right)+{b}\left({b}+\mathrm{1}\right)\right) \\ $$$$\left({a},{b},{c}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{optimal}. \\ $$$$\mathrm{Therefore},\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\sqrt{\mathrm{3}}. \\ $$

Commented by Tinkutara last updated on 28/Aug/17

Thank you very much Sir! This question can also be asked where all are unequal.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}!\:\mathrm{This} \\ $$$$\mathrm{question}\:\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{asked}\:\mathrm{where}\:\mathrm{all} \\ $$$$\mathrm{are}\:\mathrm{unequal}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com