Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20726 by Tinkutara last updated on 01/Sep/17

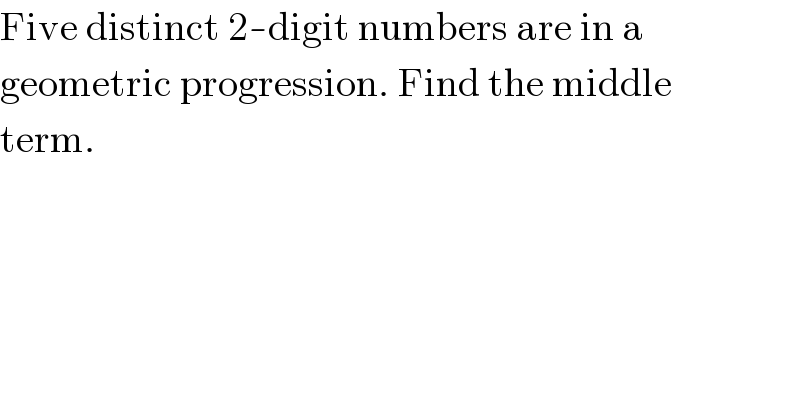
Five distinct 2-digit numbers are in a geometric progression. Find the middle term.

$$\mathrm{Five}\:\mathrm{distinct}\:\mathrm{2}-\mathrm{digit}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{in}\:\mathrm{a} \\ $$$$\mathrm{geometric}\:\mathrm{progression}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{middle} \\ $$$$\mathrm{term}. \\ $$

Answered by dioph last updated on 02/Sep/17

Let the GP be {a,qa,q^2 a,q^3 a,q^4 a} As we are looking for the middle term the order is not relevant so we can safely assume q > 1. We know that a ≥ 10 and q^4 a < 100, so q < 2. 1 < q < 2 ⇒ q = ((m+n)/n) (m<n both natural numbers) Because every term is natural, we must have: n ∣ a, n^2 ∣ a, n^3 ∣ a and n^4 ∣ a a < 100 ⇒ n ∈ {2, 3} ∗ n = 2 ⇒ a ∈ {16, 32, 64} and q = (3/2), but ((3/2))^3 ×32 = 108 > 100 and ((3/2))^2 ×64 = 144 > 100, hence in this case a = 16. ∗ n = 3 ⇒ a = 81 and q ≥ (4/3), but ((4/3))×81 = 108 > 100. Therefore, n = 2, a = 16 and q = (3/2), so GP is {16, 24, 36, 54, 81} and the answer is 36

$$\mathrm{Let}\:\mathrm{the}\:\mathrm{GP}\:\mathrm{be}\:\left\{{a},{qa},{q}^{\mathrm{2}} {a},{q}^{\mathrm{3}} {a},{q}^{\mathrm{4}} {a}\right\} \\ $$$$\mathrm{As}\:\mathrm{we}\:\mathrm{are}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{the}\:\mathrm{middle}\:\mathrm{term} \\ $$$$\mathrm{the}\:\mathrm{order}\:\mathrm{is}\:\mathrm{not}\:\mathrm{relevant}\:\mathrm{so}\:\mathrm{we}\:\mathrm{can} \\ $$$$\mathrm{safely}\:\mathrm{assume}\:{q}\:>\:\mathrm{1}. \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{that}\:{a}\:\geqslant\:\mathrm{10}\:\mathrm{and}\:{q}^{\mathrm{4}} {a}\:<\:\mathrm{100}, \\ $$$$\mathrm{so}\:{q}\:<\:\mathrm{2}. \\ $$$$\mathrm{1}\:<\:{q}\:<\:\mathrm{2}\:\Rightarrow\:{q}\:=\:\frac{{m}+{n}}{{n}}\:\left({m}<{n}\:\mathrm{both}\:\mathrm{natural}\:\mathrm{numbers}\right) \\ $$$$\mathrm{Because}\:\mathrm{every}\:\mathrm{term}\:\mathrm{is}\:\mathrm{natural},\:\mathrm{we} \\ $$$$\mathrm{must}\:\mathrm{have}: \\ $$$${n}\:\mid\:{a},\:{n}^{\mathrm{2}} \:\mid\:{a},\:{n}^{\mathrm{3}} \:\mid\:{a}\:\mathrm{and}\:{n}^{\mathrm{4}} \:\mid\:{a} \\ $$$${a}\:<\:\mathrm{100}\:\Rightarrow\:{n}\:\in\:\left\{\mathrm{2},\:\mathrm{3}\right\} \\ $$$$\ast\:{n}\:=\:\mathrm{2}\:\Rightarrow\:{a}\:\in\:\left\{\mathrm{16},\:\mathrm{32},\:\mathrm{64}\right\}\:\mathrm{and}\:{q}\:=\:\frac{\mathrm{3}}{\mathrm{2}}, \\ $$$$\mathrm{but}\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} ×\mathrm{32}\:=\:\mathrm{108}\:>\:\mathrm{100}\:\mathrm{and} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{64}\:=\:\mathrm{144}\:>\:\mathrm{100},\:\mathrm{hence} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{a}\:=\:\mathrm{16}. \\ $$$$\ast\:{n}\:=\:\mathrm{3}\:\Rightarrow\:{a}\:=\:\mathrm{81}\:\mathrm{and}\:{q}\:\geqslant\:\frac{\mathrm{4}}{\mathrm{3}},\:\mathrm{but} \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{3}}\right)×\mathrm{81}\:=\:\mathrm{108}\:>\:\mathrm{100}. \\ $$$$\mathrm{Therefore},\:{n}\:=\:\mathrm{2},\:{a}\:=\:\mathrm{16}\:\mathrm{and}\:{q}\:=\:\frac{\mathrm{3}}{\mathrm{2}}, \\ $$$$\mathrm{so}\:\mathrm{GP}\:\mathrm{is}\:\left\{\mathrm{16},\:\mathrm{24},\:\mathrm{36},\:\mathrm{54},\:\mathrm{81}\right\}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{36} \\ $$

Commented by Tinkutara last updated on 02/Sep/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com