
Question Number 20733 by Joel577 last updated on 02/Sep/17
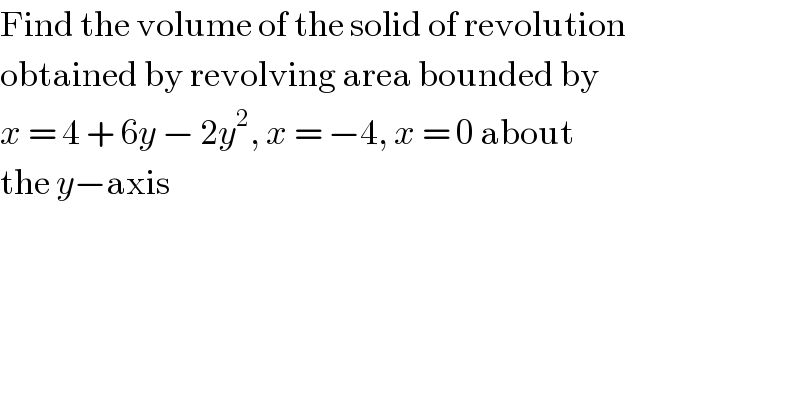
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solid}\:\mathrm{of}\:\mathrm{revolution} \\ $$$$\mathrm{obtained}\:\mathrm{by}\:\mathrm{revolving}\:\mathrm{area}\:\mathrm{bounded}\:\mathrm{by} \\ $$$${x}\:=\:\mathrm{4}\:+\:\mathrm{6}{y}\:−\:\mathrm{2}{y}^{\mathrm{2}} ,\:{x}\:=\:−\mathrm{4},\:{x}\:=\:\mathrm{0}\:\mathrm{about} \\ $$$$\mathrm{the}\:{y}−\mathrm{axis} \\ $$
Answered by mrW1 last updated on 02/Sep/17
![2y^2 −6y−4+x=0 y_(1,2) =((6±(√(36−4×2(−4+x))))/4) =((3±(√(17−2x)))/2) Δy=y_1 −y_2 =(√(17−2x)) V=∫_0 ^(−4) 2πxΔydx =2π∫_0 ^(−4) x(√(17−2x))dx let t=(√(17−2x)) ⇒x=((17−t^2 )/2) dx=−tdt V=2π∫_(√(17)) ^5 ((17−t^2 )/2)×t×(−t)dt =π∫_(√(17)) ^5 (t^2 −17)t^2 dt =(π/5)[t^5 ]_(√(17)) ^5 −((17π)/3)[t^3 ]_(√(17)) ^5 =(π/5)(5^5 −17^2 (√(17)))−((17π)/3)(5^3 −17(√(17))) =(((578)/5)(√(17))−250)(π/3) ≈237.3](Q20735.png)
$$\mathrm{2y}^{\mathrm{2}} −\mathrm{6y}−\mathrm{4}+\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{4}×\mathrm{2}\left(−\mathrm{4}+\mathrm{x}\right)}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{3}\pm\sqrt{\mathrm{17}−\mathrm{2x}}}{\mathrm{2}} \\ $$$$\Delta\mathrm{y}=\mathrm{y}_{\mathrm{1}} −\mathrm{y}_{\mathrm{2}} =\sqrt{\mathrm{17}−\mathrm{2x}} \\ $$$$ \\ $$$$\mathrm{V}=\int_{\mathrm{0}} ^{−\mathrm{4}} \mathrm{2}\pi\mathrm{x}\Delta\mathrm{ydx} \\ $$$$=\mathrm{2}\pi\int_{\mathrm{0}} ^{−\mathrm{4}} \mathrm{x}\sqrt{\mathrm{17}−\mathrm{2x}}\mathrm{dx} \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{t}=\sqrt{\mathrm{17}−\mathrm{2x}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{17}−\mathrm{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{dx}=−\mathrm{tdt} \\ $$$$\mathrm{V}=\mathrm{2}\pi\int_{\sqrt{\mathrm{17}}} ^{\mathrm{5}} \frac{\mathrm{17}−\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}×\mathrm{t}×\left(−\mathrm{t}\right)\mathrm{dt} \\ $$$$=\pi\int_{\sqrt{\mathrm{17}}} ^{\mathrm{5}} \left(\mathrm{t}^{\mathrm{2}} −\mathrm{17}\right)\mathrm{t}^{\mathrm{2}} \mathrm{dt} \\ $$$$=\frac{\pi}{\mathrm{5}}\left[\mathrm{t}^{\mathrm{5}} \right]_{\sqrt{\mathrm{17}}} ^{\mathrm{5}} −\frac{\mathrm{17}\pi}{\mathrm{3}}\left[\mathrm{t}^{\mathrm{3}} \right]_{\sqrt{\mathrm{17}}} ^{\mathrm{5}} \\ $$$$=\frac{\pi}{\mathrm{5}}\left(\mathrm{5}^{\mathrm{5}} −\mathrm{17}^{\mathrm{2}} \sqrt{\mathrm{17}}\right)−\frac{\mathrm{17}\pi}{\mathrm{3}}\left(\mathrm{5}^{\mathrm{3}} −\mathrm{17}\sqrt{\mathrm{17}}\right) \\ $$$$=\left(\frac{\mathrm{578}}{\mathrm{5}}\sqrt{\mathrm{17}}−\mathrm{250}\right)\frac{\pi}{\mathrm{3}} \\ $$$$\approx\mathrm{237}.\mathrm{3} \\ $$
Commented by Joel577 last updated on 02/Sep/17
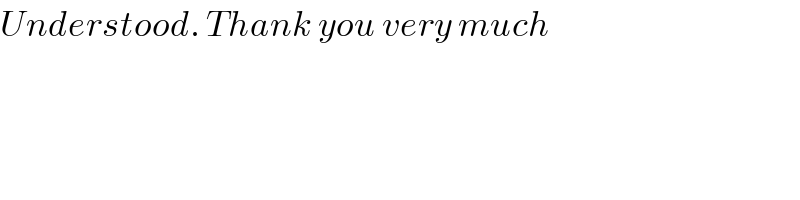
$${Understood}.\:{Thank}\:{you}\:{very}\:{much} \\ $$
Commented by mrW1 last updated on 02/Sep/17

Commented by Joel577 last updated on 02/Sep/17
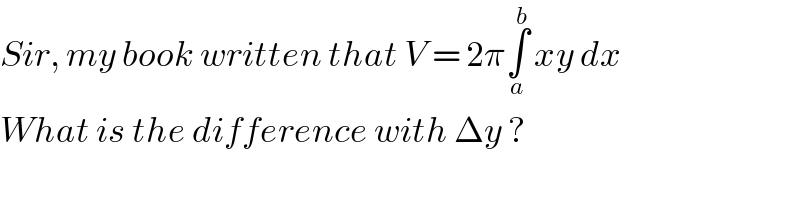
$${Sir},\:{my}\:{book}\:{written}\:{that}\:{V}\:=\:\mathrm{2}\pi\underset{{a}} {\overset{{b}} {\int}}\:{xy}\:{dx} \\ $$$${What}\:{is}\:{the}\:{difference}\:{with}\:\Delta{y}\:? \\ $$
Commented by mrW1 last updated on 02/Sep/17
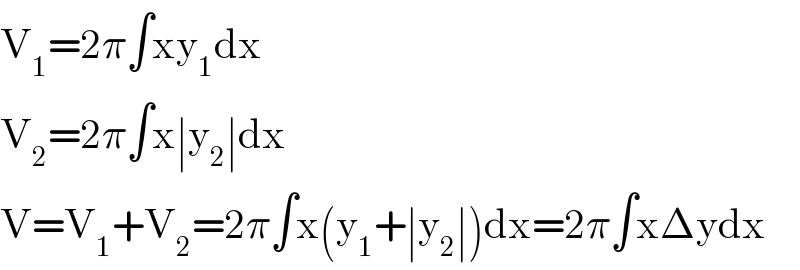
$$\mathrm{V}_{\mathrm{1}} =\mathrm{2}\pi\int\mathrm{xy}_{\mathrm{1}} \mathrm{dx} \\ $$$$\mathrm{V}_{\mathrm{2}} =\mathrm{2}\pi\int\mathrm{x}\mid\mathrm{y}_{\mathrm{2}} \mid\mathrm{dx} \\ $$$$\mathrm{V}=\mathrm{V}_{\mathrm{1}} +\mathrm{V}_{\mathrm{2}} =\mathrm{2}\pi\int\mathrm{x}\left(\mathrm{y}_{\mathrm{1}} +\mid\mathrm{y}_{\mathrm{2}} \mid\right)\mathrm{dx}=\mathrm{2}\pi\int\mathrm{x}\Delta\mathrm{ydx} \\ $$
