Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 2088 by Yozzi last updated on 01/Nov/15

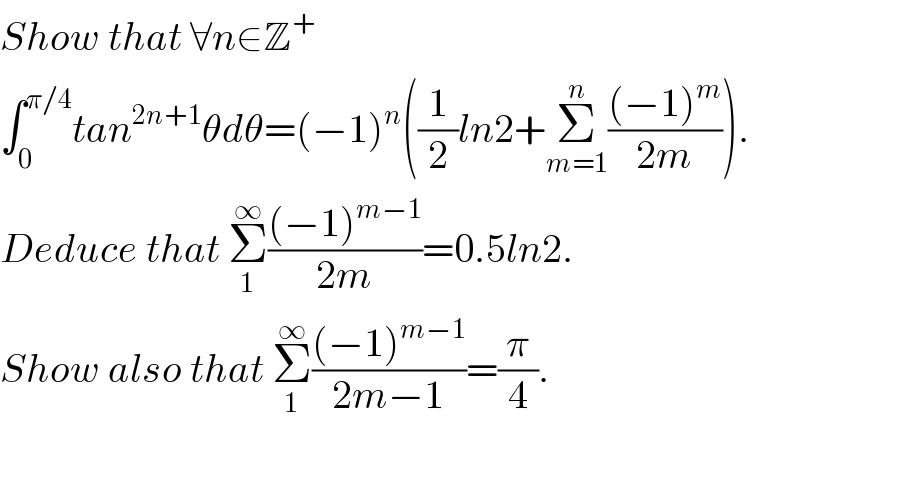
Show that ∀n∈Z^+ ∫_0 ^(π/4) tan^(2n+1) θdθ=(−1)^n ((1/2)ln2+Σ_(m=1) ^n (((−1)^m )/(2m))). Deduce that Σ_1 ^∞ (((−1)^(m−1) )/(2m))=0.5ln2. Show also that Σ_1 ^∞ (((−1)^(m−1) )/(2m−1))=(π/4).

$${Show}\:{that}\:\forall{n}\in\mathbb{Z}^{+} \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {tan}^{\mathrm{2}{n}+\mathrm{1}} \theta{d}\theta=\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{\mathrm{2}{m}}\right). \\ $$$${Deduce}\:{that}\:\underset{\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}−\mathrm{1}} }{\mathrm{2}{m}}=\mathrm{0}.\mathrm{5}{ln}\mathrm{2}. \\ $$$${Show}\:{also}\:{that}\:\underset{\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}−\mathrm{1}} }{\mathrm{2}{m}−\mathrm{1}}=\frac{\pi}{\mathrm{4}}.\: \\ $$$$ \\ $$

Commented by Yozzi last updated on 02/Nov/15

It′s an old (1990) admission exam question and I wasn′t sure where the (−1)^n factor came from. Before the part I gave here the question asked about the sketches of the graph of y=tan^k θ for k=1 and k⋙1 where x∈[0,π/4]. Your method appears to be correct. I′m wondering what went wrong...

$${It}'{s}\:{an}\:{old}\:\left(\mathrm{1990}\right)\:{admission}\:{exam} \\ $$$${question}\:{and}\:{I}\:{wasn}'{t}\:{sure}\:{where} \\ $$$${the}\:\left(−\mathrm{1}\right)^{{n}} \:{factor}\:{came}\:{from}.\: \\ $$$${Before}\:{the}\:{part}\:{I}\:{gave}\:{here}\:{the} \\ $$$${question}\:{asked}\:{about}\:{the}\:{sketches} \\ $$$${of}\:{the}\:{graph}\:{of}\:{y}={tan}^{{k}} \theta\:{for}\: \\ $$$${k}=\mathrm{1}\:{and}\:{k}\ggg\mathrm{1}\:{where}\:{x}\in\left[\mathrm{0},\pi/\mathrm{4}\right]. \\ $$$${Your}\:{method}\:{appears}\:{to}\:{be}\:{correct}. \\ $$$${I}'{m}\:{wondering}\:{what}\:{went}\:{wrong}... \\ $$$$ \\ $$

Commented by prakash jain last updated on 03/Nov/15

tan^(2n+1) θ=(tan^2 θ)^n tan θ =(sec^2 θ−1)^( n) tan θ =(−1)^n (1−sec^2 θ)^n tan θ =(−1)^n [tan θ+Σ_(m=1) ^n ^n C_m (−1)^m sec^(2m) θtan θ] =(−1)^n [tan θ+Σ_(m=1) ^n (−1)^m sec^(2m−1) θ∙sec θ∙tan θ] Integrating =(−1)^n [ln sec θ+Σ_(m=1) ^n (−1)^m ∙^n C_m ((sec^(2m) θ)/(2m))] limits 0 to (π/4) =(−1)^n [ln (√2)+Σ_(m=1) ^n (−1)^m ∙^n C_m ∙ ((2^m −1)/(2m))] more simplifications to be done.

$$\mathrm{tan}^{\mathrm{2}{n}+\mathrm{1}} \theta=\left(\mathrm{tan}^{\mathrm{2}} \theta\right)^{{n}} \mathrm{tan}\:\theta \\ $$$$=\left(\mathrm{sec}^{\mathrm{2}} \theta−\mathrm{1}\right)^{\:{n}} \mathrm{tan}\:\theta \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{1}−\mathrm{sec}^{\mathrm{2}} \theta\right)^{{n}} \mathrm{tan}\:\theta \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left[\mathrm{tan}\:\theta+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\:^{{n}} {C}_{{m}} \left(−\mathrm{1}\right)^{{m}} \mathrm{sec}^{\mathrm{2}{m}} \theta\mathrm{tan}\:\theta\right] \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left[\mathrm{tan}\:\theta+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{m}} \mathrm{sec}^{\mathrm{2}{m}−\mathrm{1}} \theta\centerdot\mathrm{sec}\:\theta\centerdot\mathrm{tan}\:\theta\right] \\ $$$$\mathrm{Integrating} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left[\mathrm{ln}\:\mathrm{sec}\:\theta+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{m}} \centerdot\:^{{n}} {C}_{{m}} \frac{\mathrm{sec}^{\mathrm{2}{m}} \:\theta}{\mathrm{2}{m}}\right] \\ $$$${limits}\:\mathrm{0}\:{to}\:\frac{\pi}{\mathrm{4}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left[\mathrm{ln}\:\sqrt{\mathrm{2}}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(−\mathrm{1}\right)^{{m}} \centerdot\:^{{n}} {C}_{{m}} \centerdot\:\frac{\mathrm{2}^{{m}} −\mathrm{1}}{\mathrm{2}{m}}\right] \\ $$$$\mathrm{more}\:\mathrm{simplifications}\:\mathrm{to}\:\mathrm{be}\:\mathrm{done}. \\ $$

Commented by prakash jain last updated on 02/Nov/15

Can you please recheck and confirm the question. Because ^n C_m (2^m −1)≠1 If the question is correct can you review the integral in comment.

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{recheck}\:\mathrm{and}\:\mathrm{confirm}\:\mathrm{the} \\ $$$$\mathrm{question}.\:\mathrm{Because}\: \\ $$$$\:^{{n}} {C}_{{m}} \left(\mathrm{2}^{{m}} −\mathrm{1}\right)\neq\mathrm{1}\: \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{can}\:\mathrm{you}\:\mathrm{review} \\ $$$$\mathrm{the}\:\mathrm{integral}\:\mathrm{in}\:\mathrm{comment}. \\ $$

Commented by prakash jain last updated on 03/Nov/15

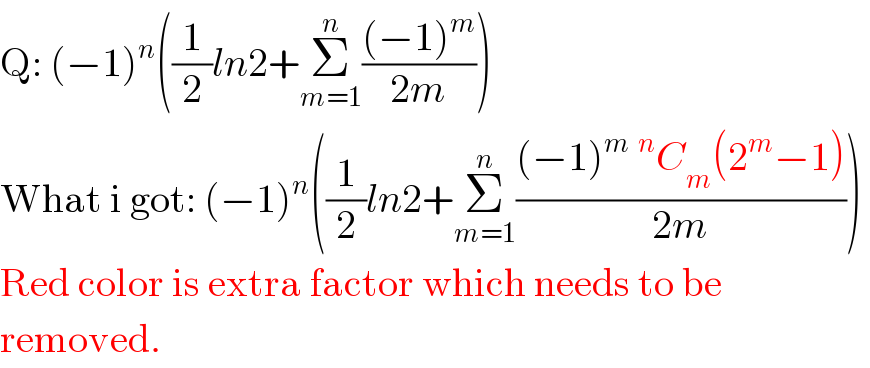
Q: (−1)^n ((1/2)ln2+Σ_(m=1) ^n (((−1)^m )/(2m))) What i got: (−1)^n ((1/2)ln2+Σ_(m=1) ^n (((−1)^m ^n C_m (2^m −1))/(2m))) Red color is extra factor which needs to be removed.

$$\mathrm{Q}:\:\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{\mathrm{2}{m}}\right)\: \\ $$$$\mathrm{What}\:\mathrm{i}\:\mathrm{got}:\:\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} \:^{{n}} {C}_{{m}} \left(\mathrm{2}^{{m}} −\mathrm{1}\right)}{\mathrm{2}{m}}\right)\: \\ $$$$\mathrm{Red}\:\mathrm{color}\:\mathrm{is}\:\mathrm{extra}\:\mathrm{factor}\:\mathrm{which}\:\mathrm{needs}\:\mathrm{to}\:\mathrm{be} \\ $$$$\mathrm{removed}. \\ $$

Commented by Yozzi last updated on 03/Nov/15

I derived a reduction formula which excludes the factor ((n),(m) ) (2^m −1) when used to prove the answer. But, I don′t know how the factor (−1)^n comes in. I_n +I_(n−1) =(1/(2n)) n≥2,I_n =∫_0 ^(π/4) tan^(2n+1) θdθ.

$${I}\:{derived}\:{a}\:{reduction}\:{formula}\:{which} \\ $$$${excludes}\:{the}\:{factor}\:\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}\:\left(\mathrm{2}^{{m}} −\mathrm{1}\right) \\ $$$${when}\:{used}\:{to}\:{prove}\:{the}\:{answer}. \\ $$$${But},\:{I}\:{don}'{t}\:{know}\:{how}\:{the}\:{factor}\:\left(−\mathrm{1}\right)^{{n}} \\ $$$${comes}\:{in}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{I}_{{n}} +{I}_{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$${n}\geqslant\mathrm{2},{I}_{{n}} =\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {tan}^{\mathrm{2}{n}+\mathrm{1}} \theta{d}\theta. \\ $$

Commented by prakash jain last updated on 03/Nov/15

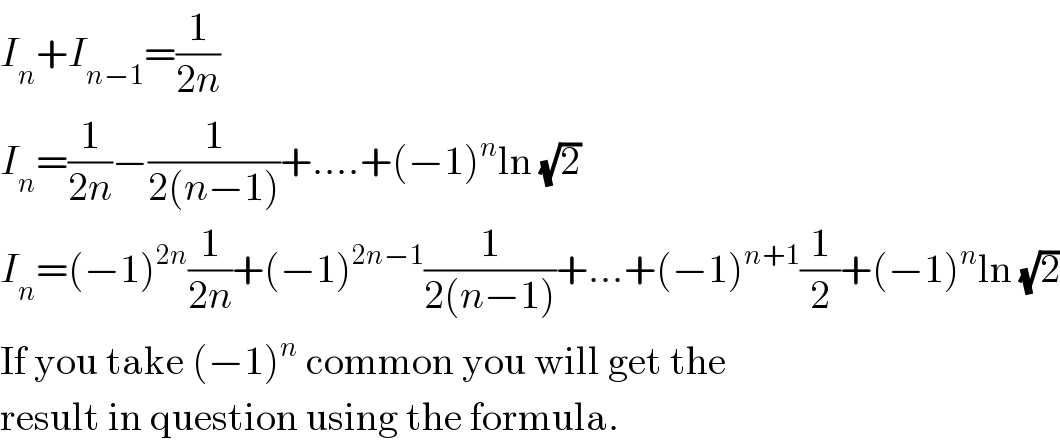
I_n +I_(n−1) =(1/(2n)) I_n =(1/(2n))−(1/(2(n−1)))+....+(−1)^n ln (√2) I_n =(−1)^(2n) (1/(2n))+(−1)^(2n−1) (1/(2(n−1)))+...+(−1)^(n+1) (1/2)+(−1)^n ln (√2) If you take (−1)^n common you will get the result in question using the formula.

$${I}_{{n}} +{I}_{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$${I}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}\left({n}−\mathrm{1}\right)}+....+\left(−\mathrm{1}\right)^{{n}} \mathrm{ln}\:\sqrt{\mathrm{2}} \\ $$$${I}_{{n}} =\left(−\mathrm{1}\right)^{\mathrm{2}{n}} \frac{\mathrm{1}}{\mathrm{2}{n}}+\left(−\mathrm{1}\right)^{\mathrm{2}{n}−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}\left({n}−\mathrm{1}\right)}+...+\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}+\left(−\mathrm{1}\right)^{{n}} \mathrm{ln}\:\sqrt{\mathrm{2}} \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{take}\:\left(−\mathrm{1}\right)^{{n}} \:\mathrm{common}\:\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{result}\:\mathrm{in}\:\mathrm{question}\:\mathrm{using}\:\mathrm{the}\:\mathrm{formula}. \\ $$

Commented by Yozzi last updated on 03/Nov/15

I see. Thanks!

$${I}\:{see}.\:{Thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com