
Question Number 2089 by Yozzi last updated on 01/Nov/15
![If x∈[0,0.5π], show that sinx≥x−(1/6)x^3 . Hence prove that (1/(3000))≤∫_0 ^(1/10) (x^2 /((1−x+sinx)^2 ))dx≤(2/(5999)).](Q2089.png)
$${If}\:{x}\in\left[\mathrm{0},\mathrm{0}.\mathrm{5}\pi\right],\:{show}\:{that}\:{sinx}\geqslant{x}−\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} . \\ $$$${Hence}\:{prove}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{3000}}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}/\mathrm{10}} \frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}+{sinx}\right)^{\mathrm{2}} }{dx}\leqslant\frac{\mathrm{2}}{\mathrm{5999}}. \\ $$
Commented by prakash jain last updated on 02/Nov/15
![sin x≥x−(x^3 /6) 0≤((x/(1−x+sin x)))^2 ≤((x/(1−x+x−(x^3 /6))))^2 ∫((36x^2 )/((6−x^3 )^2 ))dx 6−x^3 =u⇒−3x^2 dx=du ∫ ((−12du)/u^2 )=((12)/u)=((12)/(6−x^3 ))=((12000)/(5999))−2=(2/(5999)) sin x≤x x^2 ≤((x/(1−x+sin x)))^2 ∫x^2 dx=[(x^3 /3)]_0 ^(1/10) =(1/(3000)) Not a complete proof but an outline of approach.](Q2100.png)
$$\mathrm{sin}\:{x}\geqslant{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\mathrm{0}\leqslant\left(\frac{{x}}{\mathrm{1}−{x}+\mathrm{sin}\:{x}}\right)^{\mathrm{2}} \leqslant\left(\frac{{x}}{\mathrm{1}−{x}+{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}\right)^{\mathrm{2}} \\ $$$$\int\frac{\mathrm{36}{x}^{\mathrm{2}} }{\left(\mathrm{6}−{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{6}−{x}^{\mathrm{3}} ={u}\Rightarrow−\mathrm{3}{x}^{\mathrm{2}} {dx}={du} \\ $$$$\int\:\frac{−\mathrm{12}{du}}{{u}^{\mathrm{2}} }=\frac{\mathrm{12}}{{u}}=\frac{\mathrm{12}}{\mathrm{6}−{x}^{\mathrm{3}} }=\frac{\mathrm{12000}}{\mathrm{5999}}−\mathrm{2}=\frac{\mathrm{2}}{\mathrm{5999}} \\ $$$$\mathrm{sin}\:{x}\leqslant{x} \\ $$$${x}^{\mathrm{2}} \leqslant\left(\frac{{x}}{\mathrm{1}−{x}+\mathrm{sin}\:{x}}\right)^{\mathrm{2}} \\ $$$$\int{x}^{\mathrm{2}} {dx}=\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}/\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{3000}} \\ $$$$\mathrm{Not}\:\mathrm{a}\:\mathrm{complete}\:\mathrm{proof}\:\mathrm{but}\:\mathrm{an}\:\mathrm{outline}\:\mathrm{of}\:\mathrm{approach}. \\ $$
Commented by 123456 last updated on 01/Nov/15
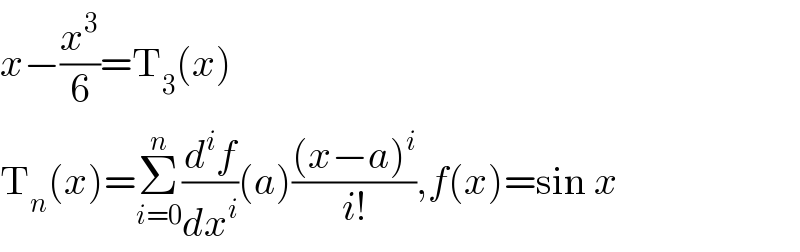
$${x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}=\mathrm{T}_{\mathrm{3}} \left({x}\right) \\ $$$$\mathrm{T}_{{n}} \left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{d}^{{i}} {f}}{{dx}^{{i}} }\left({a}\right)\frac{\left({x}−{a}\right)^{{i}} }{{i}!},{f}\left({x}\right)=\mathrm{sin}\:{x} \\ $$
Commented by prakash jain last updated on 02/Nov/15

$$\mathrm{sin}\:{x}\geqslant{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!},\:\mathrm{can}\:\mathrm{be}\:\mathrm{seen}\:\mathrm{from}\:\mathrm{sin}\:{x}\:\mathrm{series} \\ $$$$\mathrm{expansion}. \\ $$
Commented by Yozzi last updated on 02/Nov/15

$${Thanks}!\: \\ $$
