Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 21154 by youssoufab last updated on 14/Sep/17

prove: ∀n∈N^∗ ,∀(a,b)∈C^2 , a^(2n+1) +b^(2n+1) = Σ_(k=o) ^(2n) (−1)^k a^k b^(2n−k)

$${prove}:\:\forall{n}\in\mathbb{N}^{\ast} ,\forall\left({a},{b}\right)\in\mathbb{C}^{\mathrm{2}} ,\:{a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} = \\ $$$$\underset{{k}={o}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \\ $$

Commented by alex041103 last updated on 15/Sep/17

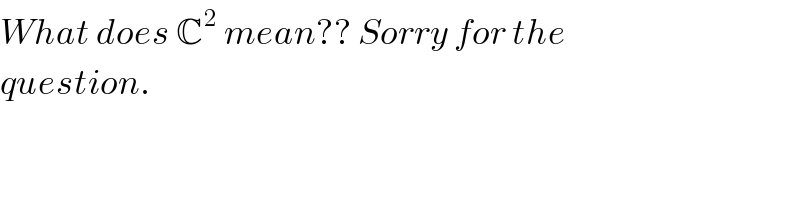
What does C^2 mean?? Sorry for the question.

$${What}\:{does}\:\mathbb{C}^{\mathrm{2}} \:{mean}??\:{Sorry}\:{for}\:{the} \\ $$$${question}. \\ $$

Commented by sma3l2996 last updated on 15/Sep/17

that′s mean a∈C and b∈C

$${that}'{s}\:{mean}\:{a}\in\mathbb{C}\:{and}\:{b}\in\mathbb{C} \\ $$

Answered by alex041103 last updated on 15/Sep/17

Let′s start with the expresion (a+b)(Σ_(k=0) ^(2n) (−1)^k a^k b^(2n−k) )= =Σ_(k=0) ^(2n) (−1)^k a^(k+1) b^(2n−k) +Σ_(k=0) ^(2n) (−1)^k a^k b^(2n+1−k) = =(−1)^(2n) a^(2n+1) b^0 +Σ_(k=0) ^(2n−1) (−1)^k a^(k+1) b^(2n−k) +(−1)^0 a^0 b^(2n+1) +Σ_(k=1) ^(2n) (−1)^k a^k b^(2n+1−k) = =a^(2n+1) +b^(2n+1) +Σ_(k=1) ^(2n) (−1)^(k−1) a^k b^(2n+1−k) +Σ_(k=1) ^(2n) (−1)^k a^k b^(2n+1−k) Because (−1)^(k−1) =(((−1)^k )/(−1))=−(−1)^k ⇒(a+b)(Σ_(k=0) ^(2n) (−1)^k a^k b^(2n−k) )= =a^(2n+1) +b^(2n+1) −Σ_(k=1) ^(2n) (−1)^k a^k b^(2n+1−k) +Σ_(k=1) ^(2n) (−1)^k a^k b^(2n+1−k) = =a^(2n+1) +b^(2n+1) Note: The statement a^(2n+1) +b^(2n+1) =Σ_(k=0) ^(2n) (−1)^k a^k b^(2n−k) is False. The true statement is that a^(2n+1) +b^(2n+1) =(a+b)[Σ_(k=0) ^(2n) (−1)^k a^k b^(2n−k) ]

$${Let}'{s}\:{start}\:{with}\:{the}\:{expresion} \\ $$$$\left({a}+{b}\right)\left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \right)= \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}+\mathrm{1}} {b}^{\mathrm{2}{n}−{k}} +\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}+\mathrm{1}−{k}} = \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{2}{n}} {a}^{\mathrm{2}{n}+\mathrm{1}} {b}^{\mathrm{0}} +\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}+\mathrm{1}} {b}^{\mathrm{2}{n}−{k}} +\left(−\mathrm{1}\right)^{\mathrm{0}} {a}^{\mathrm{0}} {b}^{\mathrm{2}{n}+\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}+\mathrm{1}−{k}} = \\ $$$$={a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {a}^{{k}} {b}^{\mathrm{2}{n}+\mathrm{1}−{k}} +\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}+\mathrm{1}−{k}} \\ $$$${Because}\:\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{{k}} }{−\mathrm{1}}=−\left(−\mathrm{1}\right)^{{k}} \\ $$$$\Rightarrow\left({a}+{b}\right)\left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \right)= \\ $$$$={a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} −\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}+\mathrm{1}−{k}} +\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}+\mathrm{1}−{k}} = \\ $$$$={a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$ \\ $$$${Note}:\:{The}\:{statement} \\ $$$${a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \\ $$$${is}\:{False}. \\ $$$${The}\:{true}\:{statement}\:{is}\:{that} \\ $$$${a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} =\left({a}+{b}\right)\left[\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \right] \\ $$$$ \\ $$

Commented by alex041103 last updated on 15/Sep/17

Note: The false statement a^(2n+1) +b^(2n+1) =Σ_(k=0) ^(2n) (−1)^k a^k b^(2n−k) is in fact allways true when a+b=1 or { ((Re(a)+Re(b)=1)),((Im(a)=−Im(b))) :} And also when a+b≠0 and a^(2n+1) +b^(2n+1) =0 (both of those are true for n≠0)

$${Note}:\:{The}\:{false}\:{statement} \\ $$$${a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \\ $$$${is}\:{in}\:{fact}\:{allways}\:{true}\:{when}\:{a}+{b}=\mathrm{1} \\ $$$${or}\:\begin{cases}{{Re}\left({a}\right)+{Re}\left({b}\right)=\mathrm{1}}\\{{Im}\left({a}\right)=−{Im}\left({b}\right)}\end{cases} \\ $$$${And}\:{also}\:{when}\:{a}+{b}\neq\mathrm{0}\:{and}\: \\ $$$${a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} =\mathrm{0}\:\left({both}\:{of}\:{those}\:{are}\:{true}\right. \\ $$$$\left.{for}\:{n}\neq\mathrm{0}\right) \\ $$

Commented by youssoufab last updated on 15/Sep/17

am sorry it is: a^(2n+1) +b^(2n+1) =(a+b)Σ_(k=0) ^(2n) (−1)^k a^k b^(2n−k) thanks flr help !

$$\mathrm{am}\:\mathrm{sorry}\:\mathrm{it}\:\mathrm{is}: \\ $$$${a}^{\mathrm{2}{n}+\mathrm{1}} +{b}^{\mathrm{2}{n}+\mathrm{1}} =\left({a}+{b}\right)\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {a}^{{k}} {b}^{\mathrm{2}{n}−{k}} \\ $$$${thanks}\:{flr}\:{help}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com