Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 113706 by Rasikh last updated on 15/Sep/20

$$\int \sqrt{\mathrm{tanx}}\mathrm{dx}=?$$

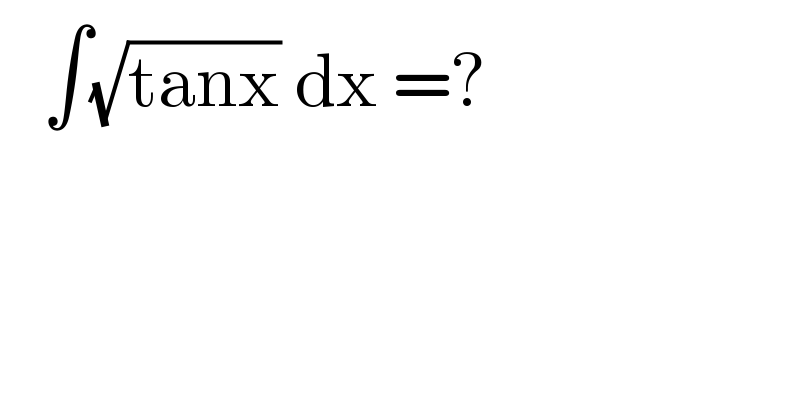
Answered by MJS_new last updated on 15/Sep/20

$$\int \sqrt{\tan x}dx=$$$$[t=\sqrt{\tan x}\to dx={2\cos }^{2}x\sqrt{\tan x}dt]$$$$=2\int \frac{t^2}{t^4+1}dt=\frac{\sqrt{2}}{2}\int (\frac{t}{t^2-\sqrt{2}t+1}-\frac{t}{t^2+\sqrt{2}t+1})dt=$$$$=\frac{\sqrt{2}}{4}\ln \frac{t^2-\sqrt{2}t+1}{t^2+\sqrt{2}t+1}+\frac{\sqrt{2}}{2}(\arctan (\sqrt{2}t-1)+\arctan (\sqrt{2}t+1))$$$$\mathrm{with}t=\sqrt{\tan x}$$

Commented by malwan last updated on 16/Sep/20

$$fantastic$$$$remember$$$$\int \frac{dx}{{ax}^2+bx+c}=$$$$\{\begin{array}{l}\frac{1}{\sqrt{b^2-4ac}}ln\frac{2ax+b-\sqrt{b^2-4ac}}{2ax+b+\sqrt{b^2-4ax}}(b^2>4ac)\\ \frac{2}{\sqrt{4ac-b^2}}{tan}^{-1}\left(\frac{2ax+b}{\sqrt{4ac-b^2}}\right)(b^2<4ac)\end{array}$$$$$$$$-\frac{2}{2ax+b}(b^2=4ac)$$

Answered by mathdave last updated on 15/Sep/20

$$solution$$$$lett=\sqrt{\tan x},t^2=\tan x,dx=\frac{2t}{1+t^4}dt$$$$I=\int \sqrt{\tan x}=\int t\times \frac{2t}{1+t^4}dt=\int \frac{2t^2}{1+t^4}dt$$$$but2t^2=(t^2-1)+(1+t^2)$$$$I=\int \frac{t^2-1}{1+t^4}dt+\int \frac{t^2+1}{1+t^4}dt=A+B$$$$letA=\int \frac{t^2-1}{1+t^4}dt=\int \frac{1-1/t^2}{t^2+1/t^2}dt$$$$lett+1/t=p.......\left(x\right)$$$$\frac{dp}{dt}=1-1/t^2,dp=(1-1/t^2)dt....\left(1\right)andfrom\left(x\right)$$$${(t+1/t)}^2=p^2,t^2+1/t^2=p^2-{\left(\sqrt{2}\right)}^2.......\left(2\right)$$$$\because A=\int \frac{dp}{p^2-{\left(\sqrt{2}\right)}^2}$$$$but\int \frac{dz}{z^2-a^2}=\frac{1}{2a}\ln \left[\frac{z-a}{z+a}\right]$$$$A=\int \frac{dp}{p^2-{\left(\sqrt{2}\right)}^2}=\frac{1}{2\sqrt{2}}\ln \left[\frac{p-\sqrt{2}}{p+\sqrt{2}}\right]=\frac{1}{2\sqrt{2}}\ln \left[\frac{t+1/t-\sqrt{2}}{t+1/t+\sqrt{2}}\right]$$$$\because \int \frac{t^2-1}{1+t^4}dt=\frac{1}{2\sqrt{2}}\ln \left[\frac{t^2-t\sqrt{2}+1}{t^2+t\sqrt{2}+1}\right]........xx$$$$andB=\int \frac{t^2+1}{1+t^4}dt=\int \frac{1+1/t^2}{t^2+1/t^2}dt$$$$lett-1/t=p,dp=(1+1/t^2)dt....\left(1\right)and$$$${(t-1/t)}^2=p^2,t^2+1/t^2=p^2+{\left(\sqrt{2}\right)}^2.....\left(2\right)$$$$\int \frac{1+1/t^2}{t^2+1/t^2}dt=\int \frac{dp}{p^2+{\left(\sqrt{2}\right)}^2}$$$$but\int \frac{dz}{z^2+a^2}=\frac{1}{a}{\tan }^{-1}\left[\frac{p}{\sqrt{2}}\right]$$$$\int \frac{t^2+1}{1+t^4}dt=\frac{1}{\sqrt{2}}{\tan }^{-1}\left[\frac{t^2-1}{t\sqrt{2}}\right]......xxx$$$$\because \int \sqrt{\tan x}dx=\frac{1}{2\sqrt{2}}\ln \left[\frac{t^2-\sqrt{2}t+1}{t^2+\sqrt{2}t+1}\right]+\frac{1}{\sqrt{2}}{\tan }^{-1}\left[\frac{t^2-1}{\sqrt{2}t}\right]$$$$\int \sqrt{\tan x}dx=\frac{\sqrt{2}}{4}\ln \left[\frac{\tan x-\sqrt{2\tan x}+1}{\tan x+\sqrt{2\tan x}+1}\right]+\frac{\sqrt{2}}{2}{\tan }^{-1}\left[\frac{\tan x-1}{\sqrt{2\tan x}}\right]+k$$$$mathdave$$$$$$

Commented by mathdave last updated on 15/Sep/20

Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\mathrm{sir}$$

Answered by mathmax by abdo last updated on 14/Sep/20

$$\mathrm{I}=\int \sqrt{\mathrm{tanx}}\mathrm{dx}\mathrm{changement}\sqrt{\mathrm{tanx}}=\mathrm{t}\mathrm{give}\mathrm{x}=\arctan \left({\mathrm{t}}^2\right)\Rightarrow$$$$\mathrm{I}=\int \frac{\mathrm{t}.\left(2\mathrm{t}\right)}{1+{\mathrm{t}}^4}\mathrm{dt}=2\int \frac{{\mathrm{t}}^2}{1+{\mathrm{t}}^4}\mathrm{dt}=2\int \frac{1}{\frac{1}{{\mathrm{t}}^2}+{\mathrm{t}}^2}\mathrm{dt}$$$$=\int \frac{1-\frac{1}{{\mathrm{t}}^2}+1+\frac{1}{{\mathrm{t}}^2}}{\frac{1}{{\mathrm{t}}^2}+{\mathrm{t}}^2}\mathrm{dt}=\int \frac{1-\frac{1}{{\mathrm{t}}^2}}{{(\mathrm{t}+\frac{1}{\mathrm{t}})}^2-2}\mathrm{dt}(\to \mathrm{t}+\frac{1}{\mathrm{t}}=\mathrm{u})+\int \frac{1+\frac{1}{{\mathrm{t}}^2}}{{(\mathrm{t}-\frac{1}{\mathrm{t}})}^2+2}\mathrm{dt}(\to \mathrm{t}-\frac{1}{\mathrm{t}}=\mathrm{v})$$$$=\int \frac{\mathrm{du}}{{\mathrm{u}}^2-2}+\int \frac{\mathrm{dv}}{{\mathrm{v}}^2+2}\mathrm{we}\mathrm{have}\int \frac{\mathrm{du}}{{\mathrm{u}}^2-2}=\frac{1}{2\sqrt{2}}\int (\frac{1}{\mathrm{u}-\sqrt{2}}-\frac{1}{\mathrm{u}+\sqrt{2}})\mathrm{du}$$$$=\frac{1}{2\sqrt{2}}\ln \mid \frac{\mathrm{u}-\sqrt{2}}{\mathrm{u}+\sqrt{2}}\mid +{\mathrm{c}}_1=\frac{1}{2\sqrt{2}}\ln \mid \frac{\mathrm{t}+\frac{1}{\mathrm{t}}-\sqrt{2}}{\mathrm{t}+\frac{1}{\mathrm{t}}+\sqrt{2}}\mid +{\mathrm{c}}_1=\frac{1}{2\sqrt{2}}\ln \mid \frac{{\mathrm{t}}^2-\sqrt{2}\mathrm{t}+1}{{\mathrm{t}}^2+\sqrt{2}\mathrm{t}+1}\mid +{\mathrm{c}}_1$$$$\int \frac{\mathrm{dv}}{{\mathrm{v}}^2+2}{=}_{\mathrm{v}=\sqrt{2}\alpha }\int \frac{\sqrt{2}\mathrm{d}\alpha }{2(1+{\alpha }^2)}=\frac{1}{\sqrt{2}}\arctan \left(\alpha \right)+\mathrm{c}2$$$$=\frac{1}{\sqrt{2}}\arctan \left(\frac{1}{\sqrt{2}}(\mathrm{t}-\frac{1}{\mathrm{t}})\right)+{\mathrm{c}}_2\Rightarrow$$$$\mathrm{I}=\frac{1}{2\sqrt{2}}\ln \mid \frac{{\mathrm{t}}^2-\sqrt{2}\mathrm{t}+1}{{\mathrm{t}}^2+\sqrt{2}\mathrm{t}+1}\mid +\frac{1}{\sqrt{2}}\arctan \left(\frac{{\mathrm{t}}^2-1}{\mathrm{t}\sqrt{2}}\right)+\mathrm{C}\mathrm{but}\mathrm{t}=\sqrt{\mathrm{tanx}}\Rightarrow$$$$\mathrm{I}=\frac{1}{2\sqrt{2}}\ln \mid \frac{\mathrm{tanx}-\sqrt{2\mathrm{tanx}}+1}{\mathrm{tanx}+\sqrt{2\mathrm{tanx}}+1}\mid +\frac{1}{\sqrt{2}}\arctan \left(\frac{\mathrm{tanx}-1}{\sqrt{2\mathrm{tanx}}}\right)+\mathrm{C}$$

Answered by john santu last updated on 15/Sep/20

$$\int \sqrt{\tan x}dx=\int \frac{\sqrt{\tan x}+\sqrt{\cot x}}{2}dx+\int \frac{\sqrt{\tan x}-\sqrt{\cot x}}{2}dx$$$$=\frac{1}{2}\int \frac{\sqrt{\sin x}}{\sqrt{\cos x}}+\frac{\sqrt{\cos x}}{\sqrt{\sin x}}dx+\frac{1}{2}\int \frac{\sqrt{\sin x}}{\sqrt{\cos x}}-\frac{\sqrt{\cos x}}{\sqrt{\sin x}}dx$$$$=\frac{1}{2}\int \frac{\sin x+\cos x}{\sqrt{\sin 2x}}dx+\frac{1}{2}\int \frac{\sin x-\cos x}{\sqrt{\sin 2x}}dx$$$$=\frac{1}{\sqrt{2}}\int \frac{\sin x+\cos x}{\sqrt{1-{(\sin x-\cos x)}^2}}dx+\frac{1}{\sqrt{2}}\int \frac{\sin x-\cos x}{\sqrt{{(\sin x+\cos x)}^2-1}}dx$$$$=\frac{1}{\sqrt{2}}\int \frac{dt}{\sqrt{1-t^2}}-\frac{1}{\sqrt{2}}\int \frac{du}{\sqrt{u^2-1}}$$$$=\frac{1}{\sqrt{2}}{\sin }^{-1}\left(t\right)-\frac{1}{\sqrt{2}}\ln (u+\sqrt{u^2-1})+c$$$$=\frac{1}{\sqrt{2}}{\sin }^{-1}(\sin x-\cos x)-\frac{1}{\sqrt{2}}\ln (\sin x+\cos x+\sqrt{\sin 2x})+c$$$$[notet=\sin x-\cos x,u=\sin x+\cos x]$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com