
Question Number 21247 by Tinkutara last updated on 17/Sep/17
![If [ ] represents the greatest integer function and f(x) = x − [x] then number of real roots of the equation f(x) + f((1/x)) = 1 are infinite. True/False](Q21247.png)
$$\mathrm{If}\:\left[\:\right]\:\mathrm{represents}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{integer} \\ $$$$\mathrm{function}\:\mathrm{and}\:{f}\left({x}\right)\:=\:{x}\:−\:\left[{x}\right]\:\mathrm{then} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$${f}\left({x}\right)\:+\:{f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\mathrm{1}\:\mathrm{are}\:\mathrm{infinite}. \\ $$$$\boldsymbol{\mathrm{True}}/\boldsymbol{\mathrm{False}} \\ $$
Answered by dioph last updated on 21/Sep/17
![x−[x] + (1/x)−[(1/x)] = 1 x = 1 is not a root. if x > 1, [(1/x)] = 0 and hence: x − [x] + (1/x) = 1 For some fixed [x]=k we have: x^2 −(k+1)x + 1 = 0 x = ((k+1±(√(k^2 +2k−3)))/2) k = 1 ⇒ x = 1 which we have already considered. k > 1 ⇒ 2k > 3 ⇒ k^2 < k^2 +2k−3 < (k+1)^2 ⇒ k+(1/2) < ((k+1+(√(k^2 +2k−3)))/2) < k+1 Hence there is one real root x for every k = [x] > 1 Because we have no further assumptions about k, the function does indeed have infinite real roots (True)](Q21358.png)
$${x}−\left[{x}\right]\:+\:\frac{\mathrm{1}}{{x}}−\left[\frac{\mathrm{1}}{{x}}\right]\:=\:\mathrm{1} \\ $$$${x}\:=\:\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{root}. \\ $$$$\mathrm{if}\:{x}\:>\:\mathrm{1},\:\left[\frac{\mathrm{1}}{{x}}\right]\:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{hence}: \\ $$$${x}\:−\:\left[{x}\right]\:+\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{1} \\ $$$$\mathrm{For}\:\mathrm{some}\:\mathrm{fixed}\:\left[{x}\right]={k}\:\mathrm{we}\:\mathrm{have}: \\ $$$${x}^{\mathrm{2}} \:−\left({k}+\mathrm{1}\right){x}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{{k}+\mathrm{1}\pm\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}{\mathrm{2}} \\ $$$${k}\:=\:\mathrm{1}\:\Rightarrow\:{x}\:=\:\mathrm{1}\:\mathrm{which}\:\mathrm{we}\:\mathrm{have}\:\mathrm{already} \\ $$$$\mathrm{considered}. \\ $$$${k}\:>\:\mathrm{1}\:\Rightarrow\:\mathrm{2}{k}\:>\:\mathrm{3} \\ $$$$\Rightarrow\:{k}^{\mathrm{2}} \:<\:{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}\:<\:\left({k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{k}+\frac{\mathrm{1}}{\mathrm{2}}\:<\:\frac{{k}+\mathrm{1}+\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}{\mathrm{2}}\:<\:{k}+\mathrm{1} \\ $$$$\mathrm{Hence}\:\mathrm{there}\:\mathrm{is}\:\mathrm{one}\:\mathrm{real}\:\mathrm{root}\:{x}\:\mathrm{for} \\ $$$$\mathrm{every}\:{k}\:=\:\left[{x}\right]\:>\:\mathrm{1} \\ $$$$\mathrm{Because}\:\mathrm{we}\:\mathrm{have}\:\mathrm{no}\:\mathrm{further}\:\mathrm{assumptions} \\ $$$$\mathrm{about}\:{k},\:\mathrm{the}\:\mathrm{function}\:\mathrm{does}\:\mathrm{indeed} \\ $$$$\mathrm{have}\:\mathrm{infinite}\:\mathrm{real}\:\mathrm{roots}\:\left(\boldsymbol{\mathrm{True}}\right) \\ $$
Commented by dioph last updated on 21/Sep/17
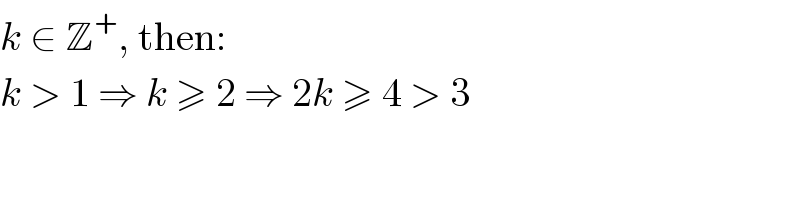
$${k}\:\in\:\mathbb{Z}^{+} ,\:\mathrm{then}: \\ $$$${k}\:>\:\mathrm{1}\:\Rightarrow\:{k}\:\geqslant\:\mathrm{2}\:\Rightarrow\:\mathrm{2}{k}\:\geqslant\:\mathrm{4}\:>\:\mathrm{3} \\ $$
Commented by Tinkutara last updated on 22/Sep/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
