Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2135 by Rasheed Soomro last updated on 04/Nov/15

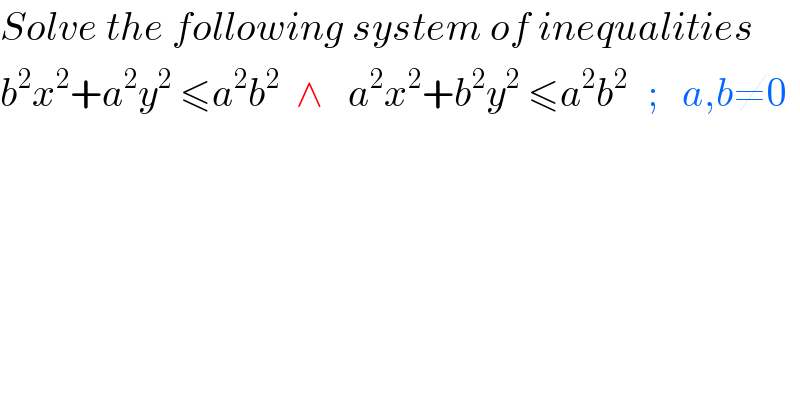
Solve the following system of inequalities b^2 x^2 +a^2 y^2 ≤a^2 b^2 ∧ a^2 x^2 +b^2 y^2 ≤a^2 b^(2 ) ; a,b≠0

$${Solve}\:{the}\:{following}\:{system}\:{of}\:{inequalities} \\ $$$${b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} \:\leqslant{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\:\wedge\:\:\:{a}^{\mathrm{2}} {x}^{\mathrm{2}} +{b}^{\mathrm{2}} {y}^{\mathrm{2}} \:\leqslant{a}^{\mathrm{2}} {b}^{\mathrm{2}\:} \:\:;\:\:\:{a},{b}\neq\mathrm{0} \\ $$

Commented by 123456 last updated on 04/Nov/15

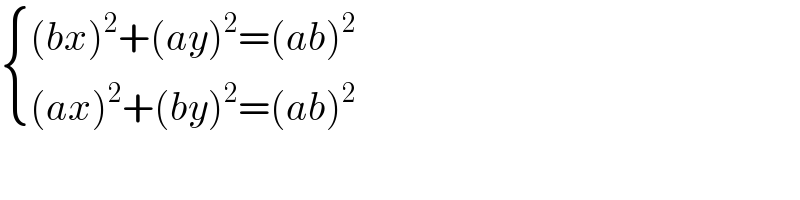
{ (((bx)^2 +(ay)^2 =(ab)^2 )),(((ax)^2 +(by)^2 =(ab)^2 )) :}

$$\begin{cases}{\left({bx}\right)^{\mathrm{2}} +\left({ay}\right)^{\mathrm{2}} =\left({ab}\right)^{\mathrm{2}} }\\{\left({ax}\right)^{\mathrm{2}} +\left({by}\right)^{\mathrm{2}} =\left({ab}\right)^{\mathrm{2}} }\end{cases} \\ $$

Answered by prakash jain last updated on 04/Nov/15

x^2 =u,y^2 =v,a^2 =c,b^2 =d Also assume c≤d du+cv=cd cu+dv=cd u=((cd)/(c+d)),v=((cd)/(c+d)) u=0, v≤c v=0, u≤c Range of u,v or x^2 ,y^2 will be inside the quadilateral (0,0),(0,c),(((cd)/(c+d)),((cd)/(c+d))),(c,0) This mapped to x,y will be within the octagon with the following points assuming a^2 ≤b^2 . (−a,0),(((−ab)/(√(a^2 +b^2 ))),((−ab)/(√(a^2 +b^2 )))),(0,−a),(((ab)/(√(a^2 +b^2 ))),((−ab)/(√(a^2 +b^2 )))), (a,0),(((ab)/(√(a^2 +b^2 ))),((ab)/(√(a^2 +b^2 )))),(0,a),(((−ab)/(√(a^2 +b^2 ))),((ab)/(√(a^2 +b^2 )))),

$${x}^{\mathrm{2}} ={u},{y}^{\mathrm{2}} ={v},{a}^{\mathrm{2}} ={c},{b}^{\mathrm{2}} ={d} \\ $$$$\mathrm{Also}\:\mathrm{assume}\:{c}\leqslant{d} \\ $$$${du}+{cv}={cd} \\ $$$${cu}+{dv}={cd} \\ $$$${u}=\frac{{cd}}{{c}+{d}},{v}=\frac{{cd}}{{c}+{d}} \\ $$$${u}=\mathrm{0},\:{v}\leqslant{c} \\ $$$${v}=\mathrm{0},\:{u}\leqslant{c} \\ $$$$\mathrm{Range}\:\mathrm{of}\:{u},{v}\:\mathrm{or}\:{x}^{\mathrm{2}} ,{y}^{\mathrm{2}} \mathrm{will}\:\mathrm{be}\:\mathrm{inside}\:\mathrm{the}\:\mathrm{quadilateral} \\ $$$$\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{0},{c}\right),\left(\frac{{cd}}{{c}+{d}},\frac{{cd}}{{c}+{d}}\right),\left({c},\mathrm{0}\right) \\ $$$$\mathrm{This}\:\mathrm{mapped}\:\mathrm{to}\:{x},{y}\:\mathrm{will}\:\mathrm{be}\:\mathrm{within}\:\mathrm{the}\:\mathrm{octagon} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{following}\:\mathrm{points}\:\mathrm{assuming}\:{a}^{\mathrm{2}} \leqslant{b}^{\mathrm{2}} . \\ $$$$\left(−{a},\mathrm{0}\right),\left(\frac{−{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }},\frac{−{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right),\left(\mathrm{0},−{a}\right),\left(\frac{{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }},\frac{−{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right), \\ $$$$\left({a},\mathrm{0}\right),\left(\frac{{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }},\frac{{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right),\left(\mathrm{0},{a}\right),\left(\frac{−{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }},\frac{{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right), \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com